
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модели такого рода позволяют изучать реальные объекты; формулировать физические законы и создавать физические теории.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Идеальный газ – см. Газ идеальный. Идеальная жидкость – воображаемая жидкость, лишенная вязкости и теплопроводности; в ней отсутствует внутреннее трение, т.е. нет касательных напряжений между двумя соседними слоями, она внутренне непрерывна и не имеет структуры. Идеальная жидкость является физической моделью реальных жидкостей. Такая модель дает хорошее описание реальных течений жидкостей и газов на достаточном удалении от омываемых твердых поверхностей и поверхностей раздела с неподвижной средой. Изобара – линия на диаграмме состояния, изображающая процесс при постоянном давлении (изобарный процесс). Изобарный (изобарический) процесс – [от греч. isos – равный и báros – тяжесть] – термодинамический процесс, происходящий в системе при постоянном давлении; на термодинамической диаграмме изображается изобарой. Для идеального газа при изобарном процессе объём пропорционален температуре. – (См. Гей-Люссака закон). Изолированная термодинамическая система - термодинамическая система, которая не обменивается с внешней средой энергией и веществом. Изотерма – линия на диаграмме состояния, изображающая изотермический процесс. Изотермический процесс – термодинамический процесс, происходящий в системе при постоянной температуре; на термодинамической диаграмме изображается изотермой. В идеальном газе при изотермическом процессе давление обратно пропорционально объёму. – (См. Бойля-Мариотта закон). Изохора – линия на диаграмме состояния, изображающая процесс, происходящий при постоянном объёме (изохорный процесс). Изохорный (изохорический) процесс [от греч. isos – равный, одинаковый и chóra – пространство] – термодинамический процесс, происходящий в системе при постоянном объеме; на термодинамической диаграмме изображается изохорой. В идеальном газе при изохорическом процессе давление пропорционально температуре. – (См. Шарля закон). Изоэнтальпийный процесс – термодинамический процесс, происходящий при постоянной энтальпии; изображается на диаграмме состояния изоэнтальпой. Изоэнтропийный процесс – термодинамический процесс, происходящий при постоянной энтропии системы; то же, что обратимый адиабатический процесс. На диаграмме состояния изображается изоэнтропой (адиабатой). Индуктивное сопротивление – часть аэродинамического сопротивления крыла, обусловленная вихрями, оси которых берут начало на крыле и направлены вниз по потоку. Эти вихри (их называют свободными) происходят от перетекания воздуха у торцов крыла из области под крылом в область над крылом. В результате в следе за крылом происходит вращение частиц вокруг осей, проходящих через частицу и параллельных местному вектору скорости потока. Свободные вихри между торцами крыла индуцируют потоки, направленные вниз, которые, налагаясь на набегающий поток, отклоняют последний вниз на некоторый угол Интеграл Бернулли – интеграл уравнения Эйлера для идеальной несжимаемой жидкости; закон сохранения энергии, справедливый вдоль линии тока. Для стационарного течения он имеет вид
где в расчёте на единицу массы
в расчёте на единицу веса
В последней форме интеграл Бернулли применяется обычно в гидравлике. Слагаемые в нём в этом случае носят названия:
постоянная Испарение – переход вещества из жидкого агрегатного состояния в газообразное (пар).
К Кавитация – образование в капельной жидкости полостей, заполненных газом, паром или их смесью (так называемых кавитационных пузырьков или каверн); нарушение непрерывности в текущей жидкости. Кавитация наблюдается в тех местах, где давление жидкости становится ниже некоторого критического значения – давления насыщенного пара этой жидкости при данной температуре. Понижение давления может происходить вследствие больших местных скоростей в потоке движущейся жидкости (гидродинамическая кавитация), либо при прохождении звуковой волны большой интенсивности (акустическая кавитация). При перемещении с потоком в область повышенного давления пузырьки начинают с большой скоростью сокращаться (схлопываться). Схлопывание сопровождается звуковым импульсом – ударной волной. Кавитация часто наблюдается в местных гидравлических сопротивлениях, неблагоприятно сказывается на работе гидравлических машин, турбин, насосов, судовых гребных винтов. Гидродинамическая кавитация характеризуется числом кавитации Замыкание кавитационных пузырьков вблизи поверхности обтекаемого тела приводит к разрушению поверхности в результате многократного воздействия на поверхность тела ударного давления, сопровождающего схлопывание кавитационных пузырьков. Это явление называется кавитационной эрозией. Кавитация также сопровождается шумом, вибрацией, ростом местных гидравлических потерь. Капельные жидкости - вода, нефть, керосин и другие малосжимаемые жидкости, обладающие определенным объемом, величина которого практически не изменяется под воздействием внешних сил. Капельные жидкости не всегда заполняют предоставленный им объем, обычно они образуют ограниченную поверхность. Капиллярное давление – разность давлений по обе стороны искривлённой поверхности раздела двух фаз (жидкость – пар или двух жидкостей), вызванная поверхностным натяжением и искривлением поверхности жидкости. Капиллярное давление – следствие действия сил поверхностного натяжения, которые направлены по касательной к поверхности, что приводит к появлению составляющей, направленной внутрь объёма контактирующих фаз. Величина капиллярного давления
Капиллярные явления – физические явления, обусловленные поверхностным натяжением на границе раздела несмешивающихся сред; обычно явления в жидкостях, вызванные искривлением их поверхности, граничащей с другой жидкостью, газом или собственным паром. Искривление поверхности приводит к появлению в жидкости дополнительного капиллярного давления, создаваемого силами поверхностного натяжения. К капиллярным явлениям относится явление изменения высоты уровня жидкости в капилляре, опущенном одним концом в жидкость, по сравнению с уровнем свободной поверхности жидкости в сосуде. Искривление поверхности жидкости в капилляре происходит в результате её взаимодействия со стенками капилляра. Если жидкость смачивает стенки капилляра, то поверхность жидкости в капилляре вогнутая, давление под ней понижено по сравнению с давлением над поверхностью на величину Кельвин (К) – единица термодинамической температуры, одна из основных в СИ. Кельвин равен 1/273,16 части термодинамической температуры тройной точки воды. 1 К=1˚С. Кельвина шкала – термодинамическая температурная шкала, названная в честь лорда Кельвина (У.Томсона), предложившего принцип построения температурной шкалы на основе второго начала термодинамики. В Кельвина шкале за начало отсчета принят абсолютный нуль температур (‒ 273,15 ˚С). Единица отсчета – 1 Кельвин; 1 К = 1 ˚С. Кинематическая вязкость (коэффициент кинематической вязкости)– отношение коэффициента динамической вязкости к плотности вещества. Единица измерения в СИ – м2/с. Кинетическая энергия - мера механического движения тел, зависящая от скоростей их движения в заданной инерциальной системе отсчета. Кинетическая энергия является скалярной величиной, равной половине произведения массы тела на квадрат скорости его поступательного движения. Кинетическая энергия системы материальных точек равна сумме кинетических энергий всех материальных точек, из которых состоит система. Кипение – процесс парообразования в жидкости, включающий рождение пузырьков пара, их рост, движение и взаимодействие; частный случай неравновесного фазового перехода первого рода. Кипение вызывается перегревом жидкости, состояние которой попадает в область выше линии равновесия жидкость – пар, или понижением давления ниже его значения на линии равновесия жидкость – пар. Клапейрона – Менделеева уравнение – см. Уравнение Клапейрона – Менделеева. Кнудсена число – см. Число Кнудсена. Конденсация – переход вещества из газообразного состояния (пара) в жидкое или твердое состояние. Конденсация происходит в условиях равновесия существующих фаз и является фазовым переходом первого рода. Конфузор – (от лат. confundo – вливаю) – участок проточного канала в виде суживающейся трубы обычно круглого или прямоугольного сечения. В случае, когда течение жидкости или газа на входе в конфузор меньше местной скорости звука, давление при переходе от широкого входного к узкому выходному сечению падает, а скорость и, следовательно, кинетическая энергия потока возрастают. Конфузор представляет собой местное гидравлическое сопротивление. Основные потери в конфузоре – потери на трение. Они определяются по формуле: Конус Маха – коническая поверхность, ограничивающая в сверхзвуковом потоке газа область, в которой сосредоточены звуковые волны (возмущения), исходящие из точечного источника возмущений. В однородном сверхзвуковом потоке газа угол α между образующими конуса Маха и его осью называется углом Маха; он связан с числом Маха M соотношением sin α = 1/M. Поверхность конуса Маха является огибающей системы звуковых волн, распространяющихся от источника возмущений. Коэффициент кинетической энергии (коэффициент Кориолиса) – выражает отношение истинного потока кинетической энергии жидкости, соответствующего неравномерному распределению скоростей в сечении, к потоку кинетической энергии, вычисленному по средней скорости: α = где c – истинное значение скорости жидкости, cср - средняя скорость по сечению, S – площадь поперечного сечения потока. Коэффициент зависит от формы эпюры скорости по сечению. Для развитого ламинарного течения в круглой цилиндрической трубе α = 2, для турбулентного – α = 1,1. Коэффициент количества движения (коэффициент Буссинеска) α0 – отношение потока количества движения жидкости через сечение Краевой угол – угол, образуемый поверхностью твердого тела и плоскостью, касательной к поверхности жидкости, граничащей с твердым телом. Равновесное значение краевого угла определяется значениями коэффициента поверхностного натяжения на границе соприкасающихся фаз. Критерии подобия – безразмерные числа, составленные из размерных физических параметров, определяющих рассматриваемые физические явления. Равенство всех однотипных критериев подобия для двух физических явлений или систем является необходимым и достаточным условием физического подобия этих систем. Уравнения, описывающие физические явления, можно привести к безразмерному виду путём введения некоторых характерных значений для каждого из определяющих физических параметров. Тогда безразмерные коэффициенты безразмерной системы уравнений, составленные из определяющих физических параметров, будут представлять собой критерии подобия рассматриваемого явления (процесса). Всякая новая комбинация из критериев подобия также представляет собой критерий подобия. Критерии подобия используются при моделировании и установлении общих физических закономерностей (критериальных зависимостей) в гидроаэромеханике, теории упругости, теплофизике и других областях физики. В гидроаэромеханике важнейшими критериями подобия являются число Рейнольдса Re, число Маха M, число Фруда Fr, число Эйлера Eu и число Струхала Sh. Критическая скорость – скорость течения среды Критическая точка – точка на диаграмме состояния веществ, соответствующая критическому состоянию, в котором две (или более) фазы, находящиеся в термодинамическом равновесии, становятся тождественными по своим свойствам. В критической точке исчезают различия в плотности и других свойствах сосуществующих фаз. Круговой процесс (цикл) – термодинамический процесс, при котором система, претерпев ряд изменений, возвращается в исходное состояние. Термодинамические параметры и характеристические функции состояния системы (внутренняя энергия, энтальпия, термодинамические потенциалы, энтропия и др.) в результате кругового процесса принимают первоначальные значения, их изменения при круговом процессе равны нулю. В результате прямого кругового процесса теплота превращается в работу, а в обратном круговом процессе работа затрачивается на перенос теплоты от менее нагретых тел к более нагретым. В технике круговые процессы применяются в качестве рабочих циклов двигателей внутреннего сгорания, различных теплосиловых и холодильных установок. Кумулятивный эффект (кумуляция) - существенное увеличение действия взрыва в определённом направлении, достигаемое специальной формой зарядов взрывчатых веществ – с выемкой конической формы, облицованной слоем металла толщиной 1 – 2 мм, в противоположной от детонатора части заряда. При инициировании взрыва сходящийся поток продуктов детонации формируется в высокоскоростную кумулютивную струю. Под действием высокого (до 10 ГПа) давления продуктов химической реакции образуется струя металла, скорость которой достигает 10 – 15 км/с, что обеспечивает ей большую пробивную силу. Л Ламинарное течение (от лат. Lamina – полоска) - упорядоченное течение вязкой жидкости или газа, при котором жидкость (газ) перемещается как бы слоями, параллельными направлению течения. Характеризуется отсутствием перемешивания между соседними слоями и пульсаций (то есть беспорядочных быстрых изменений скорости и давления). Существование ламинарного течения возможно только до определенного, критического значения числа Рейнольдса после чего течение переходит в турбулентное течение. Критическое значение числа Рейнольдса зависит от конкретного вида течения (течение в круглой трубе, обтекание шара и т. п.). Например, для течения в круглой трубе Reкр≈ 2300.
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 422; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.86.53 (0.01 с.) |

 (угол скоса потока). Подъемная сила крыла, которая по теореме Жуковского о подъемной силе должна быть направлена перпендикулярно скорости набегающего потока, отклоняется от вертикали на тот же угол
(угол скоса потока). Подъемная сила крыла, которая по теореме Жуковского о подъемной силе должна быть направлена перпендикулярно скорости набегающего потока, отклоняется от вертикали на тот же угол 
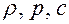 – плотность, давление и скорость жидкости,
– плотность, давление и скорость жидкости, 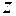 – вертикальная координата, отсчитываемая от любой горизонтальной плоскости – плоскости сравнения,
– вертикальная координата, отсчитываемая от любой горизонтальной плоскости – плоскости сравнения, 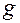 – ускорение силы тяжести,
– ускорение силы тяжести,  – постоянная, имеющая размерность давления и физический смысл полной удельной механической энергии единицы объёма жидкости. Левая часть уравнения представляет собой сумму различных видов энергии, приходящихся на единицу объёма жидкости:
– постоянная, имеющая размерность давления и физический смысл полной удельной механической энергии единицы объёма жидкости. Левая часть уравнения представляет собой сумму различных видов энергии, приходящихся на единицу объёма жидкости:  – удельная потенциальная энергия положения,
– удельная потенциальная энергия положения, 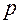 – удельная потенциальная энергия объёмного действия давления,
– удельная потенциальная энергия объёмного действия давления,  – удельная кинетическая энергия. Интеграл Бернулли можно представить в ещё в двух эквивалентных формах:
– удельная кинетическая энергия. Интеграл Бернулли можно представить в ещё в двух эквивалентных формах: ;
; 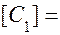 (м/с)2;
(м/с)2; м.
м. – пьезометрическая высота;
– пьезометрическая высота;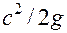 – скоростная высота (скоростной напор);
– скоростная высота (скоростной напор); – гидравлическая (полная) высота или полный напор.
– гидравлическая (полная) высота или полный напор. где
где  и
и  – давление и скорость набегающего потока,
– давление и скорость набегающего потока,  – давление насыщенного пара,
– давление насыщенного пара,  – плотность жидкости. Если число кавитации
– плотность жидкости. Если число кавитации  <
<  , то кавитация в данном месте происходит. Для местных гидравлических сопротивлений
, то кавитация в данном месте происходит. Для местных гидравлических сопротивлений  где
где 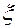 – коэффициент потерь в местном гидравлическом сопротивлении. Если известна величина
– коэффициент потерь в местном гидравлическом сопротивлении. Если известна величина  набегающего потока, при которой возникает кавитация
набегающего потока, при которой возникает кавитация  Если
Если  связана с поверхностным натяжением
связана с поверхностным натяжением  и радиусом средней кривизны поверхности жидкости
и радиусом средней кривизны поверхности жидкости  уравнением Лапласа:
уравнением Лапласа:  где
где и
и  ─ давления в жидкости 1 и контактирующей с ней среде 2,
─ давления в жидкости 1 и контактирующей с ней среде 2,  ─ поверхностное натяжение на границе двух сред.
─ поверхностное натяжение на границе двух сред. Если жидкость не смачивает стенки, то её поверхность выпуклая давление под ней выше, чем над поверхностью, жидкость в капилляре опускается ниже уровня свободной поверхности в сосуде на величину
Если жидкость не смачивает стенки, то её поверхность выпуклая давление под ней выше, чем над поверхностью, жидкость в капилляре опускается ниже уровня свободной поверхности в сосуде на величину  . Капиллярное давление уравновешивается гидростатическим давлением жидкости:
. Капиллярное давление уравновешивается гидростатическим давлением жидкости:  где
где  ─ плотность жидкости,
─ плотность жидкости,  ─ ускорение силы тяжести. Высота поднятия (опускания) жидкости в капилляре определяется по формуле:
─ ускорение силы тяжести. Высота поднятия (опускания) жидкости в капилляре определяется по формуле:  где
где  - краевой угол,
- краевой угол,  где
где 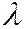 – коэффициент гидравлического трения;
– коэффициент гидравлического трения; 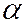 – угол сужения конфузора;
– угол сужения конфузора;  - степень сужения конфузора – отношение площади поперечного сечения канала на входе к площади на выходе из конфузора;
- степень сужения конфузора – отношение площади поперечного сечения канала на входе к площади на выходе из конфузора; 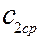 – средняя скорость течения за конфузором;
– средняя скорость течения за конфузором; 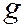 – ускорение силы тяжести. Если скорость течения на входе в конфузор превышает местную скорость звука, в нем происходит торможение потока, которое может приводить к образованию ударных волн.
– ускорение силы тяжести. Если скорость течения на входе в конфузор превышает местную скорость звука, в нем происходит торможение потока, которое может приводить к образованию ударных волн.
 , вычисленного с учётом неравномерного распределения скоростей
, вычисленного с учётом неравномерного распределения скоростей  по сечению, к потоку количества движения, вычисленного по средней скорости
по сечению, к потоку количества движения, вычисленного по средней скорости  Можно показать, что 1 ≤ α0 ≤ α, где α – коэффициент кинетической энергии.
Можно показать, что 1 ≤ α0 ≤ α, где α – коэффициент кинетической энергии. , равная местной скорости звука в данной среде. Для совершенного газа
, равная местной скорости звука в данной среде. Для совершенного газа  где
где  – показатель адиабаты,
– показатель адиабаты, 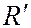 – газовая постоянная,
– газовая постоянная,  – температура торможения. Для воздуха
– температура торможения. Для воздуха  для продуктов сгорания
для продуктов сгорания 



