
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
В механике жидкости и газа уравнение состояния идеального (совершенного) газа обычно употребляют в видеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
p/ρ = RT, где ρ – плотность, R – газовая постоянная (отнесенная к единице массы, а не к молю). Уравнение Лапласа – дифференциальное уравнение в частных производных эллиптического типа. В трёхмерном пространстве в декартовых координатах имеет вид:
где
Уравнение Майера – уравнение, устанавливающее связь между молярными теплоёмкостями идеального газа при постоянном давлении Уравнения Навье-Стокса – дифференциальные уравнения движения вязкой жидкости (и газа). Для вязкой сжимаемой жидкости уравнения Навье-Стокса в проекциях на оси координат имеют вид:
где Уравнения Навье-Стокса являются наиболее общими уравнениями движения вязкой сжимаемой жидкости. С физической точки зрения они представляют собой аналог 2-го закона Ньютона: слева – произведения плотности на ускорение; справа – сумма внешних (Fx, Fy, Fz) и внутренних (давление и внутреннее трение) сил. Уравнения упрощаются в случае идеальной ( Если Для несжимаемой жидкости
В проекциях на оси координат уравнение (**) принимает вид (***):
Для несжимаемой жидкости уравнения (***) вместе с уравнением неразрывности
образуют замкнутую систему уравнений для определения u, v, w, p. Величины Если все члены уравнения (**) разделить на плотность
где В цилиндрической системе координат (
где Уравнения Навье – Стокса применяют при изучении движений реальных жидкостей и газов. Однако в силу нелинейности этих уравнений точные решения удаётся найти лишь для небольшого числа частных случаев; в большинстве конкретных задач ограничиваются отысканием приближённых решений. Уравнение неразрывности – уравнение гидродинамики, выражающее закон сохранения массы для любого объема движущейся жидкости (газа). Его дифференциальная форма
где
Для несжимаемой жидкости:
Для установившегося одномерного течения в трубе, канале и т.п. уравнение неразрывности принимает вид закона постоянства расхода Уравнение состояния – уравнение, которое связывает давление Уравнение Эйлера – дифференциальное уравнение движения идеальной жидкости в векторной форме имеет вид:
где
где Уравнения Рейнольдса для турбулентного движения несжимаемой жидкости – уравнения, используемые для описания усреднённо установившегося турбулентного течения несжимаемой жидкости. Уравнения Рейнольдса получаются из уравнений Навье – Стокса, все члены которых усредняют по времени. В проекциях на оси декартовых координат уравнения имеют следующий вид:
где Уравнение неразрывности для турбулентного течения несжимаемой жидкости после усреднения по времени имеет вид:
Ускорение жидкой частицы – векторная величина
где
Ф Фаза в термодинамике – термодинамически равновесное состояние вещества, отличающееся по физическим свойствам от других возможных равновесных состояний (других фаз) того же вещества. Переход вещества из одной фазы в другую – фазовый переход – связан с качественными изменениями свойств вещества. Например, газовое, жидкое и кристаллическое состояния (фазы) вещества различаются характером движения структурных частиц (атомов, молекул) и наличием или отсутствием упорядоченной структуры вещества. Фазовая диаграмма (диаграмма состояния) – диаграмма, изображающая зависимость устойчивого фазового состояния одно- или многокомпонентного вещества от термодинамических параметров, определяющих это состояние (температуры, давления и пр.). Каждая точка диаграммы состояния указывает на фазовый состав вещества при заданных значениях термодинамических параметров (координатах этой точки). См. также Фазовое равновесие. Фазовое равновесие – одновременное существование термодинамически равновесных фаз в многофазной системе: жидкости со своим насыщенным паром, воды и льда при температуре плавления, двух несмешивающихся жидкостей, отличающихся концентрацией. Графики, изображающие зависимость одних термодинамических параметров от других в условиях фазового равновесия, называются линиями равновесия, а их совокупность – диаграммой состояния. Линия фазового равновесия может либо пересечься с другой линией равновесия (тройная точка), либо закончиться критической точкой. Фазовый переход – переход между различными макроскопическими состояниями (фазами) многочастичной системы, происходящий при определённых значениях внешних параметров (температур, давления, напряжённости магнитного поля и т.п.). Различают фазовые переходы 1-го и 2-го рода. Фазовые переходы 1-го рода сопровождаются выделением или поглощением определённого количества теплоты, называемой теплотой фазового перехода, характеризуются постоянством температуры, изменениями энтропии и удельного объёма (происходит изменение агрегатного состояния вещества). Фазовые переходы 2-го рода не связаны с поглощением или выделением теплоты и изменением объёма, происходят непрерывным образом, характеризуются постоянством энтропии, но скачкообразным изменением теплоёмкости. Примеры фазовых переходов 2-го рода: переход ферромагнитных веществ выше точки Кюри в парамагнитное состояние, переход металлов и некоторых сплавов при температурах, близких к абсолютному нулю, в сверхпроводящее состояние. Формула Био-Савара – позволяет рассчитать поле скоростей в окрестности заданной вихревой нити L (вихревого шнура) с циркуляцией (интенстивностью) Г. Скорость, индуцированная в точке М элементом вихревой нити по формуле Био-Савара равна:
где (см. рис.) Формула Вейсбаха – формула для расчета потерь напора на местных сопротивлениях при течении несжимаемой жидкости в каналах:
где Формула Гаусса – Остроградского - математическая формула, которая выражает поток векторного поля
Формула Дарси – Вейсбаха – определяет величину потерь напора на трение при движении жидкости в круглых трубах:
где Формула Пуазейля – определяет падение давления
где Формула Сен-Венена – Ванцеля – формула, определяющая скорость
где Формула Стокса – одна из основных интегральных теорем векторного анализа, связывающая поверхностный интеграл с криволинейным; математическая формула, которая выражает циркуляцию векторного поля
Ц Центр водоизмещения – центр тяжести массы жидкости в объеме погруженной части тела. Центр давления – точка, в которой линия действия равнодействующей приложенных к покоящемуся или движущемуся телу сил давления окружающей среды (жидкости, газа) пересекается с некоторой проведенной в теле плоскостью. Например, для крыла самолета центр давления определяют как точку пересечения линии действия аэродинамической силы с плоскостью хорд крыла. Положение центра давления зависит от формы тела, а у движущегося тела от направления и скорости движения и от свойств окружающей среды (её сжимаемости). Циркуляция вектора скорости – кинематическая характеристика течения жидкости или газа, которая служит мерой завихренности течения. Циркуляция связана с вращением элементарного объема жидкости (газа) при его деформации в процессе движения. Циркуляция вектора скорости представляется криволинейным интегралом по замкнутому контуру L от произведения проекции скорости
где Если циркуляция вектора скорости по любому замкнутому контуру, проведенному внутри жидкости, равна нулю, то течение жидкости будет безвихревым, или потенциальным. Ч Число Кнудсена ( Число Маха – характеристика течения газа, равная отношению скорости течения
где Число Рейнольдса – один из критериев подобия для течений вязких жидкостей и газов, характеризующий соотношение между силами инерции и силами вязкости: Re = c Число Струхаля – критерий подобия нестационарныхдвиженийжидкости или газа, характеризует отношение локальной инерционной силы к конвективной:
где Число Фруда Fr – один из критериев подобия движения жидкостей или газов, характеризует соотношение между инерционной силой и силой тяжести:
где Число Эйлера Еи – один из критериев подобия движения жидкостей или газов, характеризующий соотношение между силами давления, действующими на элементарный объем жидкости или газа, и инерционными силами:
где Э Электрогидравлический удар - возникновение высокого давления в результате высоковольтного электрического разряда между электродами, погруженными в жидкость.
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 1794; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.104.106 (0.015 с.) |


 – неизвестная функция. С помощью дифференциального оператора Лапласа это уравнение записывается как
– неизвестная функция. С помощью дифференциального оператора Лапласа это уравнение записывается как  Функции, являющиеся решениями уравнения Лапласа, называются гармонческими. Уравнение Лапласа в механике жидкости и газа используется для нахождения потенциала скорости (задача Неймана) и функции тока (задача Дирихле). В цилиндрических координатах
Функции, являющиеся решениями уравнения Лапласа, называются гармонческими. Уравнение Лапласа в механике жидкости и газа используется для нахождения потенциала скорости (задача Неймана) и функции тока (задача Дирихле). В цилиндрических координатах  уравнение Лапласа имеет вид:
уравнение Лапласа имеет вид:
 и постоянном объёме
и постоянном объёме  :
:  где
где  – универсальная газовая постоянная.
– универсальная газовая постоянная.

 - время,
- время,  - координаты жидкой частицы,
- координаты жидкой частицы,  - проекции скорости частицы,
- проекции скорости частицы,  - плотность,
- плотность,  - давление,
- давление,  - проекции объемной силы,
- проекции объемной силы,  - коэффициент динамической вязкости.
- коэффициент динамической вязкости. =0) жидкостей.
=0) жидкостей. , то уравнение Навье-Стокса в векторной форме принимает вид (*):
, то уравнение Навье-Стокса в векторной форме принимает вид (*): 


 и
и  . С учетом этого уравнение уравнение Навье-Стокса в векторной форме принимает вид (**):
. С учетом этого уравнение уравнение Навье-Стокса в векторной форме принимает вид (**):

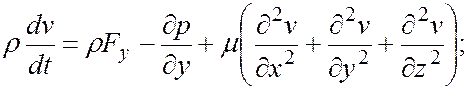


 должны быть заданы.
должны быть заданы. и представить полную производную по времени в виде суммы локальной и конвективной производных, то уравнение Навье-Стокса для несжимаемой жидкости принимает следующий вид (****):
и представить полную производную по времени в виде суммы локальной и конвективной производных, то уравнение Навье-Стокса для несжимаемой жидкости принимает следующий вид (****):
 - коэффициент кинематической вязкости.
- коэффициент кинематической вязкости. уравнения Навье – Стокса (****) имеют вид:
уравнения Навье – Стокса (****) имеют вид:


 - оператор Лапласа в цилиндрических координатах.
- оператор Лапласа в цилиндрических координатах.

 - ее скорость в данной точке. Если жидкость несжимаема (
- ее скорость в данной точке. Если жидкость несжимаема ( уравнение неразрывности принимает вид:
уравнение неразрывности принимает вид: или
или  , где
, где  - проекции скорости на оси координат. В цилиндрической системе координат (
- проекции скорости на оси координат. В цилиндрической системе координат ( уравнение неразрывности принимает вид:
уравнение неразрывности принимает вид:

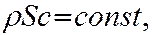 где
где 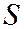 - площадь поперечного сечения.
- площадь поперечного сечения.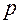 , объём
, объём  и абсолютную температуру
и абсолютную температуру  физически однородной системы в состоянии термодинамического равновесия:
физически однородной системы в состоянии термодинамического равновесия:  Примерами уравнения состояния для газов могут служить уравнение Клапейрона-Менделеева, уравнение Ван-дер-Ваальса.
Примерами уравнения состояния для газов могут служить уравнение Клапейрона-Менделеева, уравнение Ван-дер-Ваальса.
 - скорость частиц жидкости,
- скорость частиц жидкости,  - объемная сила,
- объемная сила, 


 – проекции объемной силы на оси координат. Решение общей задачи гидромеханики сводится к тому, чтобы, зная
– проекции объемной силы на оси координат. Решение общей задачи гидромеханики сводится к тому, чтобы, зная  и начальные и граничные условия, определить
и начальные и граничные условия, определить  как функции
как функции  Для этого к уравнению Эйлера присоединяют уравнение неразрывности. В случае баротропной жидкости, у которой плотность зависит только от давления, 5-м уравнением будет уравнение состояния
Для этого к уравнению Эйлера присоединяют уравнение неразрывности. В случае баротропной жидкости, у которой плотность зависит только от давления, 5-м уравнением будет уравнение состояния  (или
(или  когда жидкость несжимаема).
когда жидкость несжимаема).


 – проекции массовой силы на оси координат,
– проекции массовой силы на оси координат,  – оператор Лапласа,
– оператор Лапласа,  – проекции усреднённой скорости,
– проекции усреднённой скорости,  – проекции пульсационной составляющей скорости на оси координат.
– проекции пульсационной составляющей скорости на оси координат.

 , характеризующая изменение скорости
, характеризующая изменение скорости 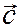 жидкой частицы с течением времени. Так как
жидкой частицы с течением времени. Так как  то
то
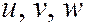 – проекции скорости на оси координат. Используя оператор Гамильтона (символический вектор набла
– проекции скорости на оси координат. Используя оператор Гамильтона (символический вектор набла  ), выражение можно представить в виде
), выражение можно представить в виде  Полное ускорение жидкой частицы равно сумме локального (местного) ускорения
Полное ускорение жидкой частицы равно сумме локального (местного) ускорения  выражающего изменение во времени скорости в фиксированной точке пространства, и конвективного ускорения
выражающего изменение во времени скорости в фиксированной точке пространства, и конвективного ускорения  выражающего изменение скорости в пространстве в данный момент времени. Локальное ускорение характеризует нестационарность поля вектора скорости, конвективное ускорение – неоднородность поля вектора скорости. Если поле стационарно – локальное ускорение равно нулю, в однородном поле равно нулю конвективное ускорение.
выражающего изменение скорости в пространстве в данный момент времени. Локальное ускорение характеризует нестационарность поля вектора скорости, конвективное ускорение – неоднородность поля вектора скорости. Если поле стационарно – локальное ускорение равно нулю, в однородном поле равно нулю конвективное ускорение.
 (*)
(*) - элемент вихревой нити,
- элемент вихревой нити,  - радиус-вектор, направленный из начала элемента вихревой нити в точку М,
- радиус-вектор, направленный из начала элемента вихревой нити в точку М,  - угол между
- угол между  направлен перпендикулярно векторам
направлен перпендикулярно векторам 
 - местная потеря напора;
- местная потеря напора;  - коэффициент местного сопротивления;
- коэффициент местного сопротивления; 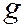 - ускорение силы тяжести. В общем случае коэффициент местного сопротивления зависит от его геометрии и режима течения (числа Рейнольдса).
- ускорение силы тяжести. В общем случае коэффициент местного сопротивления зависит от его геометрии и режима течения (числа Рейнольдса). через замкнутую поверхность
через замкнутую поверхность  через интеграл от дивиргенции этого поля по объёму
через интеграл от дивиргенции этого поля по объёму  , ограниченному этой поверхностью:
, ограниченному этой поверхностью: .
.
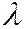 - коэффициент гидравлического трения,
- коэффициент гидравлического трения,  и
и  - длина и диаметр трубы,
- длина и диаметр трубы,  на участке круглой цилиндрической трубы длиной
на участке круглой цилиндрической трубы длиной 
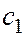 истечения газа из резервуара через сужающееся сопло (размеры резервуара считаются настолько большими по сравнению с размером отверстия сопла, что газ в резервуаре можно считать покоящимся):
истечения газа из резервуара через сужающееся сопло (размеры резервуара считаются настолько большими по сравнению с размером отверстия сопла, что газ в резервуаре можно считать покоящимся):

 и
и  – давление и температура газа в резервуаре,
– давление и температура газа в резервуаре,  – давление за соплом,
– давление за соплом, 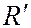 – газовая постоянная,
– газовая постоянная,  – показатель адиабаты. При давлении на срезе сопла
– показатель адиабаты. При давлении на срезе сопла  где
где  – критическое давление, скорость истечения газа из резервуара достигнет максимального значения, равного критической скорости
– критическое давление, скорость истечения газа из резервуара достигнет максимального значения, равного критической скорости  при данных параметрах газа в резервуаре:
при данных параметрах газа в резервуаре: 
 через поток ротора этого поля через поверхность
через поток ротора этого поля через поверхность 
 .
.
 где
где  – высота уровня жидкости, отсчитываемая от центра отверстия;
– высота уровня жидкости, отсчитываемая от центра отверстия;  , меньший единицы. Тогда формула приобретает вид:
, меньший единицы. Тогда формула приобретает вид:  . Множитель
. Множитель 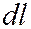 :
:

 - циркуляция вектора скорости по контуру L,
- циркуляция вектора скорости по контуру L,  через произвольную поверхность
через произвольную поверхность 
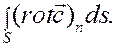
 )– один из критериев подобия движения разреженных газов,
)– один из критериев подобия движения разреженных газов,  , где
, где  – средняя длина свободного пробега молекулы в газе,
– средняя длина свободного пробега молекулы в газе,  – характерный размер течения. Если
– характерный размер течения. Если  к скорости звука
к скорости звука 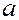 в той же точке потока:
в той же точке потока: 
 . Число Маха является одним из основных критериев подобия в гидроаэромеханике и является мерой влияния сжимаемости газа на его движение. Можно показать, что
. Число Маха является одним из основных критериев подобия в гидроаэромеханике и является мерой влияния сжимаемости газа на его движение. Можно показать, что  ~
~  , т.е. относительное изменение плотности в газовом потоке пропорционально
, т.е. относительное изменение плотности в газовом потоке пропорционально 
 0 газ можно считать несжимаемым; при
0 газ можно считать несжимаемым; при  связано с приведенной скоростью
связано с приведенной скоростью  и относительной скоростью
и относительной скоростью  следующими соотношениями:
следующими соотношениями:
 – показатель адиабаты.
– показатель адиабаты. , где c – характерная скорость потока,
, где c – характерная скорость потока, 
 - характерный линейный размер течения,
- характерный линейный размер течения,  - характерная скорость течения,
- характерная скорость течения,  - характерный для нестационарного движения промежуток времени.
- характерный для нестационарного движения промежуток времени.

 где
где  (
( – удельная теплоемкость при постоянном давлении,
– удельная теплоемкость при постоянном давлении,  – удельная теплоемкость при постоянном объеме).
– удельная теплоемкость при постоянном объеме).


