Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Fig. 2. Diagrammatic representation of lithium atom.Содержание книги
Поиск на нашем сайте
External electron is rather wide apart from a nucleus and from two electrons of internal shell – i.e. from the atomic core. The dimensions of this atomic core as it was found earlier are rather small - about 0,364RB (table 1). Therefore it is possible to consider, that valent electron is in the field of a total positive unit charge of atomic core. In this respect such atoms are hydrogen-like. It would seem that this external electron should completely replicate the behavior of electron in atom of hydrogen and satisfy formulas (3-6). But it is not exactly so. If radius of the external electron shell of lithium atom is as one of hydrogen (n=1) so its ionization potential would be equal to the ionization potential of hydrogen (13,6 eV). But lithium ionization potential is only 5,39 eV and specifies that the radius of external electron shell of atom of lithium is essentially (in 2,523 times) more, than of hydrogen. It follows from formula (5), which shows interdependence of electron energy in atom of hydrogen (numerically equal to potential of ionization) and radius of its electron orbit:
It means that external shell of lithium atom should contain more than one spatial period, and number n should be more then 1. But assuming n=2, we obtain too big distance R equal to four Bohr radiuses. The ionization potential with such distance should be equal 3,4 eV, that mismatches actual value 5,39 eV. Nevertheless, this situation has the logical settlement. Let's determine wave length of electron proceeding from its kinetic energy which, as we saw, numerically corresponds to ionization potential. Hence
So we receive wave length of electron and corresponding radius
Substituting in (15) ionization potential of lithium 5,39 eV, we get:
Here we used new notation R λ for conditional radius (spatial phase factor), parameter characterizing rate of spatial wave change. Actually this parameter was used already in formula (2). As we expected, the external electron shell of lithium atom is characterized by number (n=1,593) which, unlike hydrogen (n=1), is not integer and is in an interval between 1 and 2! However actually the external electron shell of lithium atom also is resonant and is characterized by the integral number of wave-lengths. It is achieved due to excitation of higher harmonic. That is, some unknown to us the integer number of wave-lengths N1, describing a shell resonance, should be result of multiplication of number 1,593 by other number N2 - number of harmonic. Therefore we should make some simple calculations and select suitable numbers. For example, having divided number N1=8 by n=1,593, we receive N2=5,02, that is, the fifth harmonic enables to obtain eight wave-lengths resonance of electron shell of lithium atom. Moreover the formula (4) for real shell radius appears valid when n is not an integer number
This value really meets actual magnitude of external electron shell radius of lithium atom, starting from formula (13)
There are many atoms similar to lithium with one electron on the external electron shell, so we have an opportunity to make analogous calculations in these cases too. Results of all calculations are shown in table 2. We attach such importance to these calculations to be convinced of natural character of results. Data represented in table 2 let us make a conclusion on validity of hypothesis. The nature, really, uses resonances generated on multiple harmonics, therefore atoms become more compact and in electron shells meanwhile can be "placed" greater number of electrons! Table 2
Here it is necessary to stipulate, that figures in the right column of table 2 were obtained by trial-and-error method and should be confirmed by further researches (for example, by studying spatial symmetry of chemical compounds with these atoms). In particular, numbers N1 and N2, obviously, can have values multiple of the numbers specified in the table.
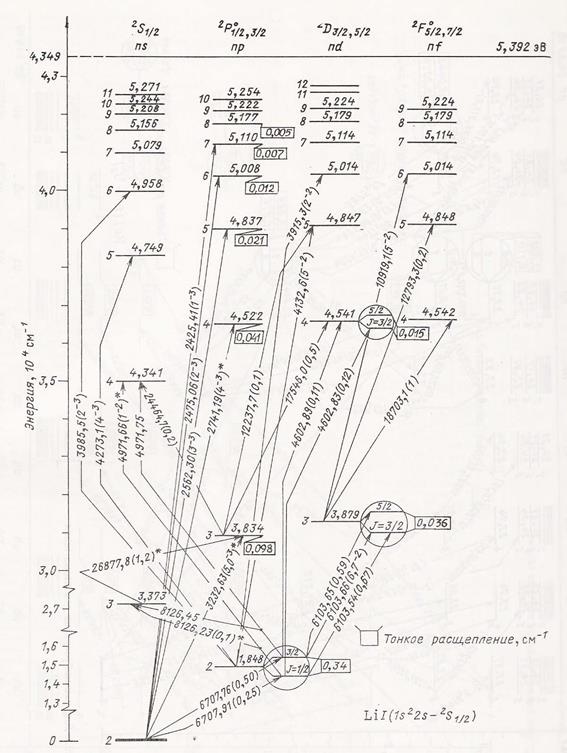
However it is not so important, whether there will be numbers multiple or commensurable as in any case these findings are extremely important for atom structure understanding. Similar laws became apparent in characteristics of the excited states of atoms, and, hence, they can be used for the analysis and systematization of atoms spectra. As an example let us examine spectrum of lithium atom. On fig. 3 there is Grotrian diagram of lithium atom [4] which represents excited states (energy levels) and transitions between them. It is necessary to make some additional calculations to ease analysis of the diagram. First, energy levels in this case are more suitable for measuring not from the lowest level corresponding ionization energy (as it is on the diagram), but from "absolute" zero (that is, from energy level at infinite separation from atom). Secondly, we will need to calculate all the same electron characteristics at excited levels, as it was done in table 2. Final table 3 includes also the principal quantum number n (the first column) which is attributed to each excited level on the diagram (fig. 3). It was made to have opportunity of comparison with the results of calculating n (relation N1/N2). Displayed in table 3 data are rather eloquent. Calculated values of the principal quantum number (n calc.) in most cases with good accuracy coincide with integer figures in the first column by which the corresponding excited levels on Grotrian diagram are marked.
Fig. 3. Grotrian diagram of lithium atom [4]. However in six cases (almost each third excited level) authors of the diagram, probably, could not be sure with the principal quantum number because it should be fractional (N1/N2), instead of integer as it is specified on the diagram. Thus numbers N1 and N2 are detected with good accuracy by means of simple calculations. Impressive also is the remoteness (R/RB) of external electron from atom nucleus at high excited levels (large n).
Table 3
In more complex atoms spectra thousands excited levels are observed, and to analyze them is much more difficult task. Besides fractional principal quantum numbers there are also other "complicating" factors. In particular, energy of the excited level is influenced by disturbing factor in the form of various mutual spin states of atomic core and external electron.
Naturally, greater work to detail parameters of all electron shells of atoms is needed. These extremely interesting and important questions, undoubtedly, will attract attention of many researchers.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-07-19; просмотров: 201; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.159.47 (0.01 с.) |

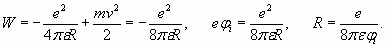 (13)
(13)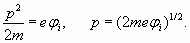 (14)
(14)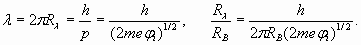 (15)
(15)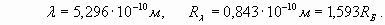
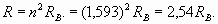 (16)
(16)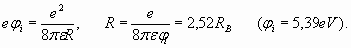 (17)
(17)