Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Волну можно мысленно разделить на слои, повторяющие движение воды.Содержание книги
Поиск на нашем сайте
Как это происходит? Замедление течения воды при увеличении поперечного сечения потока, как уже отмечалось, приводит к возникновению сил инерции и увеличению давления. Соответственно увеличивается давление на дно и вода, “отталкиваясь” от дна, устремляется вверх с нарастающей скоростью. Поэтому мысленно выделенные вертикальные столбы воды “вытягиваются”, устремляясь вверх. Таким образом, происходит преобразование кинетической энергии воды в потенциальную энергию. На другом склоне солитона происходит обратный процесс: вода спускается вниз, и ее потенциальная энергия возвращается потоку. Описанную динамику жидкости можно в какой-то степени сопоставить с движением солитона на веревке. Разбив мысленно воду на горизонтальные слои (рис. 19), мы увидим, что действующие в воде силы можно интерпретировать как центробежные силы, возникающие в результате движения воды по изогнутым траекториям. Правда, в этом случае центробежные силы не трансформируются в натяжение (как на веревке), а вызывают изменение давления внутри жидкости. Центральная часть волны превращается в мощный насос, всасывающий в себя воду и удерживающий ее наверху (рис 20).
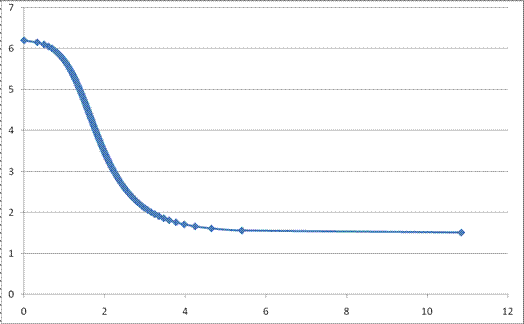
Рис. 20. Центробежные силы направлены в противоположные стороны у основания и у вершины волны. Поэтому, когда волна подходит к берегу, и глубина воды уменьшается, этот колоссальный “насос” начинает испытывать недостаток воды. Солитон втягивает в себя остатки воды, которая отступает от берега. Из-за недостатка воды та часть энергии, которая тратилась на “выкачивание” воды из глубины, идет на увеличение высоты волны при одновременном уменьшении длины самой волны. Дальнейшее развитие этого процесса приводит к обрушению воды на берег. Однако читатель справедливо заметит, что снижение давления центробежными силами в центральной части солитона компенсируется увеличением давления из-за нарастающего “утолщения” слоев к центру солитона (рис. 19). И это действительно так. Поэтому нам придется “измерить” реальное давление под солитоном, тем более, что для этого у нас есть все возможности. После того, как была определена форма солитона, а соответственно и скорость воды, мы можем составить уравнение, подобное уравнению (47), но при этом “первую точку” для уравнения опять взять у поверхности воды в стороне от солитона, а “вторую точку” – у дна непосредственно под солитоном:
Здесь учтено, что рядом с дном (нулевая высота) вода имеет только горизонтальную составляющую скорости (правая часть уравнения), как и у поверхности невозмущенной части воды (слева).
а)
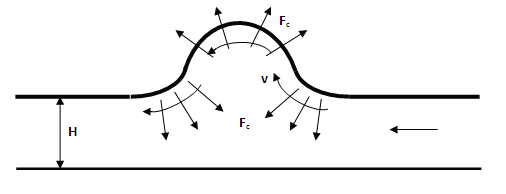
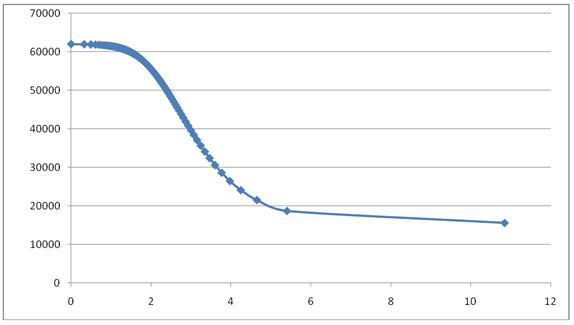
б) Рис.21. а - форма солитона, б – давление на дно при Н=1,5 и ρ=1000 (без учета атмосферного давления).
Так как у поверхности воды давление можно считать равным атмосферному давлению, то из (50) получаем следующее выражение для величины давления на дне под солитоном:
Все входящие величины известны из предыдущих вычислений, поэтому нам остается лишь добавить в расчеты еще один столбец и построить график для величины давления в зависимости от горизонтальной координаты. Эффекты, вызванные вертикальной составляющей скорости, о которых говорилось выше, становятся заметными, когда солитон выходит на малую глубину. На рис. 21 приведены результаты расчета формы солитона и давления на дно непосредственно под солитоном при тех же условиях, что и ранее, но глубина воды взята равной 1,5 (плотность воды – 1000). Кроме того, взято в расчет только давление воды (без атмосферного давления). При сравнении графиков легко заметить, что давление на дно под солитоном растет явно быстрее, чем увеличивается высота воды на склоне солитона. Чтобы оценить этот эффект, вычтем давление собственно толщи воды (ρ gh) из общей величины давления и посмотрим, что получится (рис. 22).
Рис. 22.
|
||
|
Последнее изменение этой страницы: 2021-07-19; просмотров: 167; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

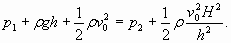 (50)
(50)
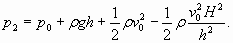 (51)
(51)