Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Факты и промежуточные выводы:Содержание книги
Поиск на нашем сайте
- Кроме атома водорода, расчеты, основанные на модели резонансных электронных оболочек атомов, дают хорошее совпадение с экспериментальными данными для ближайших к ядру электронных оболочек (n =1) всех атомов. - Электрон в атоме, находясь на замкнутой траектории, образно говоря, “попадает в резонанс сам с собой”. Если же два электрона находятся на одной общей траектории, то они образуют общий резонанс и оба “встраиваются” в него, располагаясь в разных пучностях резонанса.
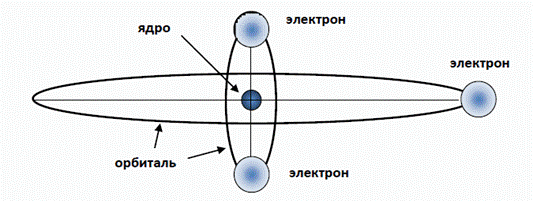
Резонансные электронные оболочки водородоподобных атомов В своих знаменитых “Лекциях” Р.Фейнман неоднократно говорил о том, что решение сложной задачи полезно начать с анализа простых частных случаев, тем более, что общее решение зачастую является комбинацией частных решений. Однако главным достоинством такого подхода является возможность получать точные результаты и “не пропустить” важные закономерности, которые могут “потеряться” в погрешностях и сложностях общего решения. Именно таким “частным случаем”, удобным для получения наиболее точных результатов, являются водородоподобные атомы. Начнем с атома лития. Ядро атома лития имеет заряд, равный трем зарядам электрона и, таким образом, вторая (внешняя) оболочка представлена всего одним электроном (рис. 2).
Рис. 2. Схематическое изображение атома лития. Внешний электрон оказывается на сравнительно большом расстоянии от ядра и от двух электронов внутренней оболочки – остова атома. Размеры этого остова, как было установлено ранее, невелики и составляют около 0,364RB (таблица 1). Поэтому можно считать, что валентный электрон находится в поле суммарного единичного положительного заряда остова атома. Казалось бы, этот внешний электрон должен полностью повторять поведение электрона в атоме водорода и удовлетворять выражениям (3-6). Но этого не происходит. Если бы радиус внешней оболочки лития был как у атома водорода (n =1), то и его потенциал ионизации был бы равен потенциалу ионизации водорода (13,6 эВ). Но у лития потенциал ионизации составляет всего 5,39 эВ и указывает на то, что радиус внешней электронной оболочки атома лития существенно (в 2,523 раза) больше, чем у водорода. Это следует из выражения (5), которое связывает между собой энергию электрона в атоме водорода (численно равную потенциалу ионизации) с радиусом орбиты электрона:
Значит, внешняя оболочка лития должна содержать больше, чем один пространственный период, и число n должно быть больше единицы. Но, положив n =2, мы получим слишком большое расстояние R, равное четырем радиусам Бора. Потенциал ионизации при таком расстоянии должен быть равен 3,4 эВ, что не соответствует фактической величине 5,39 эВ. Тем не менее, эта ситуация имеет логичное разрешение. Определим длину волны электрона, исходя из величины его кинетической энергии, которая, как мы видели, численно также соответствует потенциалу ионизации. Следовательно
Отсюда получаем длину волны электрона и радиус орбиты
Подставляя в (15) потенциал ионизации лития 5,39 эВ, получаем:
Здесь нами введено новое обозначение Rλ для условного радиуса (обратная величина волнового коэффициента), являющегося показателем скорости пространственных волновых изменений. Фактически эта величина фигурирует уже в формуле (2). Как мы и ожидали, внешняя электронная оболочка лития характеризуется числом (n =1,593), которое в отличие от водорода (n =1), не является целым и находится в промежутке между 1 и 2! Однако в действительности внешняя электронная оболочка лития также является резонансной и характеризуется целым количеством длин волн. Достигается это за счет возбуждения более высокочастотной гармоники. То есть, некоторое неизвестное нам целое число длин волн N1, характеризующее резонанс оболочки, должно быть результатом умножения числа 1,593 на другое число N2 - номер гармонической составляющей. Поэтому здесь есть некоторый элемент неопределенности, и нам придется сделать несколько простых расчетов и подобрать подходящие цифры. Например, поделив число N1=8 на n=1,593, мы получаем N2=5,02, то есть, пятая гармоника позволяет получить восемь длин волн для резонанса электронной оболочки лития. При этом формула (4) для реального радиуса оболочки оказывается справедливой и при значении n, отличном от целого числа
Эта величина действительно соответствует реальному значению радиуса внешней электронной оболочки лития, получающемуся из выражения (13)
Так как атомов, подобных литию, с одним электроном на внешней электронной оболочке довольно много, то мы имеем возможность провести аналогичные расчеты и для них. Результаты всех расчетов сведены в таблице 2. Мы уделяем этим расчетам так много внимания, чтобы убедиться в закономерном характере результатов. Приведенные в таблице 2 данные позволяют сделать вывод о справедливости сделанного предположения. Природа, действительно, использует в электронных оболочках резонансы, возбуждаемые на кратных гармонических составляющих, в результате чего атомы оказываются более компактными и, в то же время, обладают способностью “разместить” в электронных оболочках большое количество электронов! Таблица 2
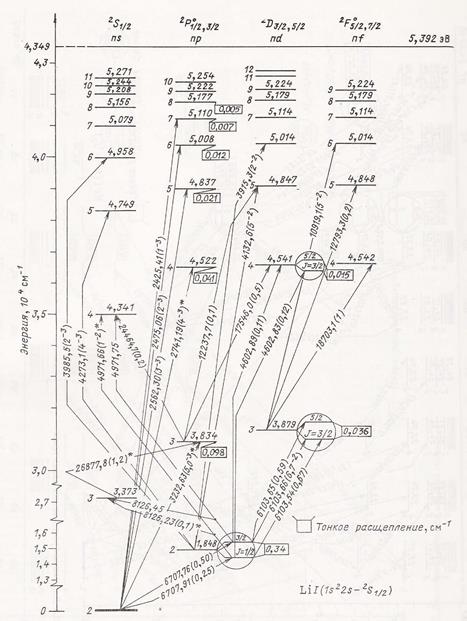
Здесь следует сразу оговориться, что цифры в правом столбце таблицы 2 получены подбором и должны быть подтверждены в ходе дальнейших исследований (например, путем изучения пространственной симметрии соединений, образуемых этими атомами). В частности, числа N1 и N2, очевидно, могут иметь значения, кратные указанным в таблице числам. Однако с принципиальной стороны не столь важно, будут ли эти числа кратными или соизмеримыми, так как в любом случае полученные результаты демонстрируют нам чрезвычайно важную закономерность строения атомов. Аналогичные закономерности проявляются и в характеристиках возбужденных состояний атомов, а, следовательно, они могут быть использованы для анализа и систематизации спектров поглощения (излучения) атомов. В качестве примера рассмотрим спектр атома лития. На рис. 3 изображена диаграмма Гротриана для атома лития [4], которая изображает совокупность возбужденных энергетических уровней и переходов между ними.
Рис. 3. Диаграмма Гротриана для атома лития [4]. Для удобства анализа этой диаграммы необходимо произвести некоторые дополнительные вычисления. Во-первых, уровни энергии нам удобнее отсчитывать не от самого низкого уровня, соответствующего энергии ионизации (как это сделано на диаграмме), а от “абсолютного” нуля (то есть, от энергии на бесконечном расстоянии от атома). Во-вторых, нам потребуется посчитать все те же характеристики электрона на возбужденных уровнях (оболочках), что и в таблице 2. Итоговая таблица 3 включает в себя также главное квантовое число n (первый столбец), которым помечен каждый возбужденный уровень на диаграмме (рис. 7). Это сделано для сравнения с расчетным n (отношением N 1 / N 2). Таблица 3
Результаты, отраженные в таблице 3, весьма красноречивы. Расчетные величины главного квантового числа (n расч.) в большинстве случаев с хорошей точностью совпадают с целочисленными величинами (первый столбец), которыми отмечены соответствующие возбужденные уровни на диаграмме Гротриана. Однако в шести случаях (почти по каждому третьему возбужденному уровню) составители диаграммы, видимо, долго не могли определиться с главным квантовым числом, так как оно должно быть дробным (N 1 / N 2), а не целым, как это указано на диаграмме. При этом числа N 1, и N 2 определяются с хорошей точностью простыми расчетами. Обращает на себя внимание “впечатляющая” удаленность (R/RB) внешнего электрона от ядра атома на высоких возбужденных уровнях (при больших n). В более сложных спектрах атомов наблюдаются тысячи возбужденных уровней, и разобраться в них намного сложнее. Кроме дробности главного квантового числа существуют и другие “усложняющие” факторы. В частности, на энергию возбужденных уровней влияет возмущающее воздействие в виде различных взаимных спиновых состояний остова и внешнего электрона. Естественно, предстоит очень большая работа по подробному описанию свойств и определению параметров всех электронных оболочек атомов. Эти чрезвычайно интересные и важные вопросы, несомненно, привлекут к себе внимание исследователей.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-07-19; просмотров: 124; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.43.109 (0.01 с.) |

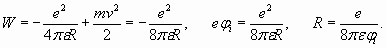 (13)
(13)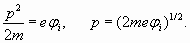 (14)
(14)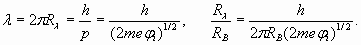 (15)
(15)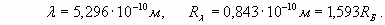
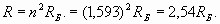 (16)
(16)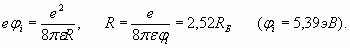 (17)
(17)