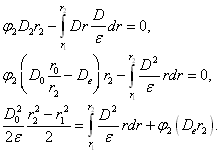Продольные электромагнитные волны внутри солитона

 

Составим уравнение, аналогичное уравнению (2.5), но в отличие от него, вместо эффективного значения напряженности электрического поля используем “обычную” величину напряженности D/ε. Такая замена связана с тем, что в действительности динамические напряжения, вызывающие отличную от нуля дивергенцию поля, ориентированы перпендикулярно к направлению деформации вихрей. К этому выводу мы пришли в предыдущем разделе, когда рассматривали механизм возникновения дивергенции электрического поля (заряда).

Эти напряжения между концентрическими слоями динамической области напоминают “трение” между слоями и порождают силы между вихрями, направленные не в радиальном, а в азимутальном направлении.

Поэтому вместо (2.5) получим

Преобразуем уравнение (3.1) и запишем его в следующем виде:

В отличие от уравнения (2.6), уравнение (3.2) аналитически не решается. Зависимость D(r), полученная методом численного интегрирования этого дифференциального уравнения, представлена на рис. 8.

Она практически совпадает с ранее полученной зависимостью для усредненного решения (рис. 7). Поэтому на рис. 9 показан результат вычитания усредненного варианта из полученного решения. Для максимально возможного исключения так называемой ошибки усечения при получении результата вычитания, оба дифференциальных уравнения (2.5) и (3.1) были решены одним и тем же численным методом Эйлера.

Отметим, что колебания, показанные на рис. 9, названы радиальными колебаниями в связи с тем, что они являются результатом вычитания усредненного поля (со строго азимутальным направлением распространения) из общей картины поля с учетом радиальных колебаний.

Рис. 8. Зависимость динамического электрического смещения

от радиуса (колебательный вариант).

 

Почему мы делаем вывод о наличии радиальных колебаний в динамической области? Дело в том, что поток электромагнитной энергии (вектор Умова-Пойнтинга), связанный с образованием ненулевой дивергенции поля, очевидно, направлен радиально. Это векторное произведение напряженности электрического поля (силы), имеющей в этом случае азимутальное направление, на вектор магнитного поля (вращения), направленного вдоль оси солитона (рис. 6).

Рис. 9. Радиальные колебания электрического поля

В динамической области.

 

Остановимся на этом вопросе несколько подробнее.

Форма записи уравнения (3.2) дает возможность понять, о каких динамических напряжениях между слоями идет речь, и каким образом возникает отличная от нуля дивергенция поля. На рис. 10 близкая к полупериоду синусоиды форма солитона (п. 2) аппроксимирована равнобедренным треугольником (развертка по длине пути вращения солитона). Крутизна переднего и заднего фронтов одиночной волны характеризуется ротором электрического поля. Он должен равняться константе ± D_о/2εr_o (рис. 10, б), чтобы обеспечивать однородную (в сечении, перпендикулярном к направлению распространения) величину магнитного поля, то есть, не зависящую от изменения радиуса.

Но этот ротор как раз равен левой части уравнения (3.2)! Численное решение уравнения (рис. 8) показывает, что ротор напряженности электрического поля для произвольного значения радиуса (D/2εr) может как превышать, так и быть меньше величины D_о/2εr_o (рис. 11). Таким образом, вторая составляющая в правой стороне уравнения (3.2) “сглаживает” неоднородность ротора электрического поля на переднем и заднем фронтах солитона. Это означает, что вихри, испытывающие воздействие более крутого фронта воздействуют на вихри из соседнего слоя с меньшей крутизной фронта и “подкручивают” их (эти силы имеют азимутальное направление подобно силам трения между концентрическими слоями).

 

Рис. 10. Развертка азимутального изменения электрического смещения в динамической области солитона.

 

а — реальная (предполагаемая) форма одиночной волны солитона,

б — аппроксимация волны солитона, l — развертка траектории вращательного движения солитона. (rot E = ± D_о/2εr_o имеет противоположные знаки на переднем и заднем фронтах солитона и соответствует крутизне этих фронтов на нижней схеме.)

 

Посмотрим на эти процессы еще с одной стороны.

Энергия, связанная с отличной от нуля дивергенцией электрического поля, может быть выражена, исходя из выражения (3.2), следующим образом:

Величина Ψ₀ = 2 D_оr_о соответствует набегу фазы (или величине пути, пробегаемого точкой поверхности вращающегося вихря) при прохождении солитона. Она делится поровну между задним и передним фронтами (по D_оr_о). Энергия, аккумулируемая за счет дивергенции электрического поля, равна работе сил, действующих со стороны вихрей соседних слоев. А именно, результирующий ротор сил умножается на набег фазы (D_оr_о) вихря за время движения переднего фронта.

При прохождении заднего фронта солитона знаки роторов сил меняются на противоположные, и эта энергия расходуется на то, чтобы притормозить (или ускорить) вращение вихрей в соседних слоях динамической области, в которых ротор электрического поля отличается от среднего значения.

 

 

Рис. 11. Ротор напряженности электрического поля для произвольного значения радиуса ( D/2εr ) может как превышать, так и быть меньше величины D_о/2εr_o, принятой на графике за единицу.

Для иллюстрации процессов, происходящих при вращении солитона, мы использовали самую простую форму для аппроксимации огибающей одиночной волны. Однако это не имеет принципиального значения, так как при любой форме фронтов роторы напряженности электрического поля будут пропорциональны отношениям текущих значений величин поля и радиуса (D/r). Поэтому указанная неоднородность роторов сил сохранится.

Изучая механизм вращательного движения поля, незаметно для себя мы обнаружили неисследованный вид поля — стоячие продольные электромагнитные колебания. Действительно, энергия, связанная с отличной от нуля дивергенцией поля (рис. 12), передается в радиальном направлении, то есть, вдоль направления электрического поля от одного концентрического слоя к другому и обратно.

Интересно, что интегрирование (φdivD)/2 в целом по динамической области дает нуль. Заметим, что для упрощения записи мы, как правило, ведем расчеты для цилиндра единичной высоты, а множители 2π опускаем. А если говорить еще точнее, то, имея дело с солитоном, мы должны под этим подразумевать интегрирование по каким-то очень малым секторам (2π/N).

Рис. 12. Зависимость (φdivD)/2 от радиуса.

В целом по динамической области энергия, связанная с ненулевой

дивергенцией поля, равна нулю.

 

То есть, имеет место равенство:

Справедливость этого утверждения несложно показать простыми выкладками. Действительно, после интегрирования по частям интеграла в выражении (3.3) получаем:

 

Так как потенциал на внутренней границе динамической области равен нулю, то (3.4) с учетом выражений (3.5) и (2.13) приобретает следующий вид:

 

 

Присмотревшись к уравнению (3.8), легко заметить, что оно выражает очевидное равенство общей электрической энергии (левая сторона уравнения) сумме энергий в динамической и электростатической областях.

Выражение (3.4) следует и непосредственно из уравнения (3.3), если его умножить на 2r и проинтегрировать. В результате интегрирования выражение в скобках в правой части даст нуль, так как оно равно разности между значениями потенциала на внешней границе динамической области, получаемыми для усредненного варианта и для решения с учетом радиальных колебаний. Однако оба эти варианта предусматривают получение одинаковых потоков энергии в азимутальном направлении, описывая движение солитона как целого, и поэтому потенциал j ₂ для двух вариантов один и тот же (2.13).

 

Постоянная тонкой структуры

 

Постоянная тонкой структуры в сравнении с единицей – довольно маленькое число (α ≈ 1/137,036), что дает возможность физикам при различного рода вычислениях использовать разложения по степеням этой константы и получать результаты с приемлемой точностью.

Малое значение константы α в значительной степени облегчило и нашу задачу построения модели солитона. В рассматриваемой модели константа должна выражаться отношением толщины тонкого вращающегося слоя электромагнитного поля к диаметру вращения α ≈ (r₂-r₁)/2r₀, так как именно от этого отношения зависит заряд солитона, а, следовательно, и интенсивность электромагнитного взаимодействия между солитонами.

Но можем ли мы, исходя из модели солитона, показать справедливость этого утверждения?

Сначала ответим на вопрос о том, каковы физические причины, определяющие столь малую величину постоянной тонкой структуры.

Понимание сути явления в данном случае особенно важно, так как мы должны быть уверены в правильности модели. Получение же точного численного результата, как это нередко бывает, может оказаться лишь случайным совпадением.

Внимательный читатель, конечно, уже обратил внимание на то, что радиальные колебания в солитоне (рис. 9) удивительным образом напоминают колебания подвешенной цепи. И это сходство, как мы увидим, не является только внешним.

Проведем сравнение физических механизмов этих процессов.

Колебания подвешенной цепи (гибкой нити) описывают, используя второй закон Ньютона для малого участка длины Δ x:

 

где T – сила натяжения цепи;

F_y - поперечная составляющая силы натяжения цепи;

m - масса погонного метра цепи;

g - ускорение свободного падения;

x - расстояние от нижнего конца цепи.

 

Отсюда получаем дифференциальное уравнение для колебаний цепи:

Это уравнение отличается от обычного волнового уравнения (1.1) наличием дополнительного члена, содержащего первую производную, и описывает распространение волны с изменяющейся амплитудой. Скорость этой волны тоже зависит от координаты и по аналогии с (1.1) равна

 

 

Из рис.11 следует, что равенство (4.3) выполняется с достаточной точностью. Форма собственных колебаний цепи определяется функциями Бесселя, но узловые точки колебаний с хорошей точностью могут быть определены по времени распространения сигнала, измеряемому в полу периодах (или в единицах p). На рисунке показаны колебания цепи и соответствующее время распространения волны.

Как видно из (4.3), скорость увеличивается при увеличении силы натяжения цепи (mgx), то есть, при приближении к месту подвеса и уменьшается до нуля при приближении к свободному концу цепи.

Приблизительно то же самое происходит с радиальными колебаниями в солитоне. Посмотрим на структуру уравнения (3.2)

В правой части уравнения находятся две составляющих величины ротора сил, действующих на вихрь – первая относится к обычному поперечному полю, а вторая к продольным (радиальным) колебаниям.

Рис. 11 Колебания подвешенной цепи и время распространения