Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Разложение веса элементарного отрезка веревки на тангенциальную и радиальную составляющие.
Прежде всего, заметим, что внизу у самого основания волны натяжение веревки Т равно нулю. Действительно, если бы это было не так, то волна имела бы еще большую высоту, “приподняв” дополнительно участок веревки соответствующего веса. Далее, разложив вес mgdl самого первого от основания волны участка веревки элементарной длины dl на тангенциальную Ptи радиальную Pr составляющие, приступим к составлению баланса сил, действующих на этот первый очень малый участок. Итак, радиальная составляющая веса
будет уравновешена соответствующей центробежной силой
Здесь длина элементарного участка dl выражена через радиус кривизны R веревки в этом месте и соответствующее элементарное изменение угла dα. Приравнивая (20) и (21), получаем, что угол фронта волны α, если отступить от основания волны на небольшое расстояние dl, уже будет отличаться от α0 на величину dα 1
Кроме того, появится и небольшое натяжение веревки, равное тангенциальной составляющей веса первого элементарного отрезка:
Этот первый шаг, пожалуй, самый трудный, а все дальнейшие шаги значительно проще и делаются “автоматически”. Отличие только в том, что последующие элементарные отрезки будут дополнительно испытывать на себе, как уже отмечалось, воздействие силы натяжения веревки, которая (вместе с радиальной составляющей веса) будет противостоять центробежной силе:
Поэтому вместо (22) получим:
На эту величину происходит уменьшение величины крутизны волны при очередном небольшом шаге вдоль веревки dl и соответственно происходит коррекция величин проекций веса (радиальной и тангенциальной) следующего элементарного отрезка, а также величины натяжения веревки. После того, как получены эти скорректированные значения, все оказывается готовым для следующего шага вычислений, и мы продвигаемся по веревке еще на один шаг. Таким образом, шаг за шагом, мы получаем все интересующие нас параметры волны: форму волны, ее общую высоту и силу натяжения веревки. При построении соответствующих кривых учитывалось, что значительно проще не откладывать элементарные участки длины пошагово с соответствующим углом, а воспользоваться проекциями на вертикальную и горизонтальную оси:
Такой расчет был сделан в программе Microsoft Excel. В качестве конкретных исходных данных взяты следующие цифры: dl =0,1, m =1, v =10, g =10, α 0 = π /3. После определения формы волны был осуществлен второй этап расчетов, связанный с подсчетом потенциальной и кинетической энергии каждого элементарного отрезка веревки и соответствующих суммарных величин по всей волне. Далее не составило никакого труда методом подбора величины α 0 добиться равенства суммарной потенциальной энергии волны ее суммарной кинетической энергии. Таким образом, были определены все основные параметры одиночной волны, распространяющейся по веревке, растянутой на земле. В частности, оказалось, что угол α 0 составляет величину, близкую к 73о, а скорость связана с высотой и ускорением свободного падения соотношением:
Как видим, численный коэффициент в формуле (27) действительно отличается незначительно от полученного нами ранее приближенного значения 1,173 в формуле (3). У многих такие приближенные численные методы оставляют чувство неудовлетворенности, так как они привычно стремятся к получению аналитического решения. Но фактически мы уже давно вступили в эпоху компьютерных расчетов, которые на практике доказали свою надежность и возможность не менее наглядного представления результатов. Впрочем, для любителей аналитических вычислений мы получим и дифференциальное уравнение, описывающее одиночную волну на веревке. А теперь посмотрим на результаты расчетов.
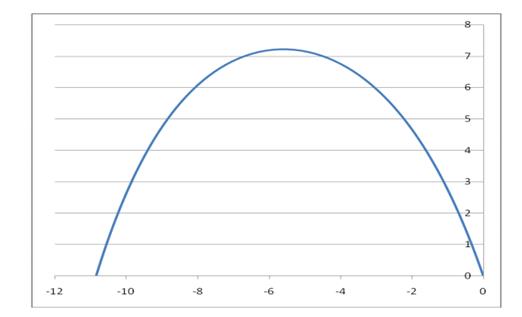
Рис. 11. Форма одиночной волны y (x) на веревке, растянутой на земле.
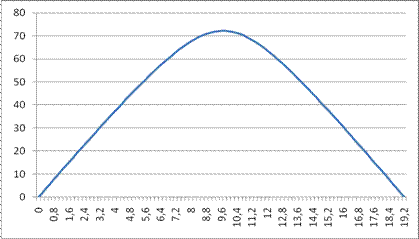
Рис. 12. Натяжение T (l) вдоль веревки в одиночной волне. На рис. 12, в отличие от рис. 11, по оси ординат отложена длина веревки в волне, а не координата х. Поэтому и значения по горизонтальной оси разные. Чтобы получить дифференциальное уравнение для одиночной волны, воспользуемся уже полученными ранее формулами (20) – (26). С учетом формулы (26) перепишем формулы (20) и (23) в виде:
Тогда натяжение веревки Т, складывающееся из тангенциальных составляющих веса элементарных участков dPt (23), будет равно:
Так как
то с учетом (29) выражение (30) запишем в виде:
Окончательно искомое дифференциальное уравнение выглядит так:
Решение этого уравнения, очевидно, ничем не отличается от полученного ранее результата. Впрочем, расчеты, проведенные ранее, более информативны, так как содержат сведения о нескольких существенных параметрах. Например, очень важной оказывается информация о натяжении веревки в пределах волны (рис. 12), так как именно эта зависимость дает ответ на вопрос об устойчивости солитона. Действительно, нестабильности, возникающие в волне, не могут выйти за пределы самой волны, поскольку натяжение веревки монотонно уменьшается до нуля при смещении от центра волны к периферии. Вследствие этого любые возмущения, приближаясь к периферии волны, теряют скорость и не могут выйти за ее пределы. Еще одной важной особенностью полученного решения является выполнение с хорошей точностью упоминавшегося ранее условия (7):
Этот баланс сил записан для самой нижней части волны – у основания, где, как уже говорилось выше, отсутствует натяжение веревки. Что касается точности расчетов, то они были проведены в довольно упрощенном варианте: длина шага dl =0,2 при длине веревки L =19,2, то есть, всего 91 шаг. И наконец, мы должны упомянуть другую сторону баланса сил (33) у самого основания одиночной волны. Как известно, “действие равно противодействию”, и в противовес “подъемной” силе будет существовать сила, обращенная вниз. В результате этой обратной реакции волна оказывает давление всем своим весом на землю, то есть, солитон отнюдь не является чем-то “невесомым”. Совершенно аналогичным образом давит на землю уже упоминавшееся ранее гибкое кольцо, которое быстро катится и сохраняет за счет этого почти круглую форму. Казалось бы, натяжение поднимает колесо, а отнюдь не прижимает его к земле (веревка и не может передавать сжимающие усилия). Тем не менее, вес колеса действует на землю как раз посредством обратной реакции, возникающей в месте прогиба колеса при контакте с землей (рис. 4). Но в этом случае, в отличие от одиночной волны, необходимо учитывать, что натяжение веревки в нижней части “гибкого колеса” при быстром качении не равно нулю. В завершение этой части рассуждений заметим, что силы трения “сковывают свободу” волны, но на скользкой поверхности она вообще не смогла бы существовать. Она бы деформировалась и разрушилась! Таким образом, рассмотренное решение, удовлетворяющее всем требованиям к солитону, на практике реализуется только путем создания специальных условий. Другими словами, мы исследовали искусственно поддерживаемое явление. Но при этом мы также убедились, что эта простая модель солитона весьма эффективна и наглядна с точки зрения демонстрации его свойств.
Солитоны на мелкой воде Насколько полученные выше закономерности для одиночных волн на веревке могут быть полезными при рассмотрении солитонов на воде? Насколько похожи друг на друга эти физические явления? Сходство достаточно очевидно, так как эти волны могут существовать исключительно благодаря гравитации, и соответственно формулы для скорости движения этих волн оказываются очень похожими друг на друга (скорость приблизительно пропорциональна корню квадратному из высоты волны).
Однако, внутренняя динамика солитона на мелкой воде намного сложнее. Именно поэтому идеи Рассела встретили непонимание даже со стороны крупных ученых того времени Эри и Стокса, а наиболее точное описание явления было получено только в 1895 году. Это сделали голландские ученые Дидерик Иоханнес Кортевег и его ученик Густав де Фриз [4]. Правда, их исследование и полученное в результате уравнение, именуемое теперь КдФ – уравнением, тоже оказались забытыми еще почти на 70 лет. Более того, основное свойство уединенной волны (вести себя подобно частице) очень долгое время оставалось незамеченным, так как все, начиная с самого Рассела, считали ее только волной. И только в 1965 году американцы М. Крускал и Н. Забуски ввели термин “солитон”, подчеркивающий подобие этой волны частице [5]. Исследования упомянутого основного свойства и доказательство устойчивости солитона потребовало больших усилий физиков и математиков. И эти усилия были вознаграждены тем, что в математике появился новый раздел, посвященный солитонам, а физики обнаружили, что уравнения и свойства уже известных солитонов могут быть распространены на многие другие явления. В частности, оказалось, что свойствами солитонов обладают такие разные явления как импульсы в нервных волокнах и вращающиеся вихри в идеальной воде. Замечательное математическое описание солитонов с появлением ЭВМ позволило достаточно подробно изучить их свойства, а математическое моделирование самых разных процессов, происходящих с солитонами, включая их столкновения между собой, очень интересно и вызывает восхищение [6]. Но очевидные успехи в математическом описании солитонов, как мы уже говорили, существенным образом потеснили представление о солитоне, как о физическом явлении. Теперь солитон воспринимается в большей степени через математические уравнения, описывающие это явление природы. Поэтому, ни в коей мере не умаляя математической стороны вопроса, нам хотелось бы на качественном уровне с минимумом математики посмотреть с физической точки зрения на некоторые свойства солитона на мелкой воде (“родоначальника” всех солитонов), столь красочно описанного Расселом. Еще со школьных времен многие, наверное, помнят опыт с водой, протекающей по трубе, диаметр которой меняется с меньшей величины на большую величину и обратно (рис. 13). При этом давление жидкости на участке трубы, имеющей большее сечение, оказывается существенно больше, чем на участках трубы с меньшим сечением [7].
Такое изменение давления объясняется тем, что при переходе потока воды в трубу с большим сечением ее скорость резко уменьшается, а при переходе на меньшее сечение - возрастает. Возникающие силы инерции при изменении скорости воды как раз и вызывают указанную разницу в давлениях.
Рис. 13.
|
||||||||
|
Последнее изменение этой страницы: 2021-07-19; просмотров: 77; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.97.189 (0.016 с.) |
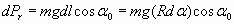 (20)
(20)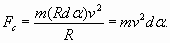 (21)
(21)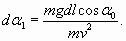 (22)
(22)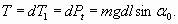 (23)
(23)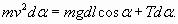 (24)
(24) (25)
(25) (26)
(26) (27)
(27)
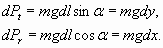 (27)
(27) (28)
(28) Соответственно формула (25) примет вид:
Соответственно формула (25) примет вид: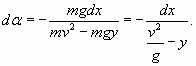 (29)
(29)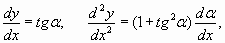 (30)
(30)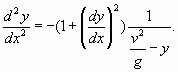 (31)
(31)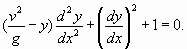 (32)
(32)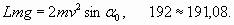 (33)
(33)