Натяжение веревки в пределах одиночной волны можно моделировать вращающимся кольцом.
Правда, левую и правую нижние части волны нужно бы поменять местами, а направление движения верхней части – на противоположное. Но натяжение веревки в месте прохождения волны действительно напоминает эффект катящегося кольца. В чем заключается этот эффект?
Посмотрим на процесс из движущейся вместе с волной системы координат. Сразу становится очевидным, что поднимающей и поддерживающей волну силой является центробежная сила, действующая в верхней части волны. Действительно, в этой части движение веревки происходит по дуге, выпуклость которой направлена вверх, чем и определяется наличие “подъемной” силы.
В то же время нижняя часть вращающегося кольца (две четверти окружности) тянет вниз, уравновешивая центробежные силы верхней части волны. Фактически картина очень напоминает накачанную камеру велосипедного колеса. Только вместо сжатого воздуха в данном случае работают центробежные силы, действующие во все стороны (как и накачанный воздух). Естественно, чем быстрее катится кольцо, тем быстрее оно вращается, и тем сильнее действие центробежных сил, усиливающих эффект “накачанного колеса” (рис. 4).
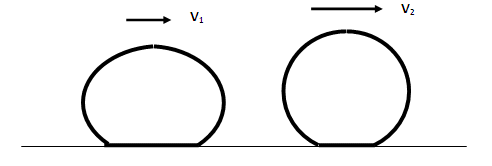
Рис. 4.
Чем больше скорость кольца (v 2 больше, чем v 1), тем более “накачанным” оно кажется.
Говоря о возможной некорректности причисления к солитонам одиночной волны, распространяющейся вдоль веревки, я как раз имел ввиду возможность нарушения основных признаков солитона. Например, сила трения веревки о землю будет препятствовать “автоматическому” увеличению высоты волны, если кинетическая энергия волны превысит потенциальную энергию. То есть, может возникнуть ситуация, аналогичная описанной выше с быстро катящимся кольцом. Чем больше будет скорость движения, тем сильнее будет натяжение веревки, а соответствующего увеличения высоты волны не произойдет.
В то же время, даже катящееся кольцо из веревки (рис. 4) при малой скорости (когда оно сильно проседает) напоминает солитон при условии равенства друг другу кинетической и потенциальной энергий этого кольца, что обеспечивается “правильным” соотношением высоты этой своеобразной волны и скорости движения. Поэтому, обращаясь к описанию одиночной волны на веревке, мы рассчитываем не на реальные опыты с неизбежными “огрехами”, а на мысленные идеальные эксперименты.
Посчитаем теперь кинетическую и потенциальную энергии волны, бегущей по веревке, с учетом простейшей аппроксимации ее формы. На рис. 5 видны четыре участка веревки в пределах волны, которые совершенно одинаковы с точки зрения подсчета кинетической энергии. Поэтому, если скорость волны обозначить через v, а массу одного погонного метра веревки - m, то кинетическая энергия будет равна умноженному на четыре интегралу вдоль одной четверти длины окружности радиусом R:
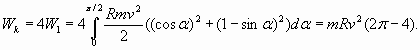 (1) (1)
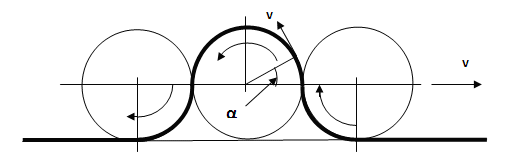
Рис. 5.
|