
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Посадка судна и ее параметрыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
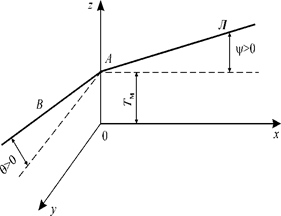
Посадкой судна называется положение его по отношению к поверхности спокойной воды. В общем случае посадка характеризуется системой параметров Тм , θ и ψ (рис. 1.4), предложенной В. Г. Власовым, в которой Тм - расстояние ОА от основной плоскости до точки пересечения произвольной ватерлинии с осью Oz (θ - угол крена, составляемый следом АВ ватерлинии на плоскости мидель - шпангоута с осью Оу (положительный при наклонении на правый борт); ψ - угол дифферента, составляемый следомВЛ ватерлинии на ДП с осью Ох (положительный при дифференте на нос). Параметры посадки Власова получили в статике корабля наибольшее распространение, так как они измеряются в главных плоскостях теоретического чертежа, что очень удобно.
Рис. 1.4 Параметры посадки судна
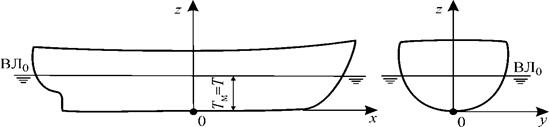
Рассмотрим некоторые частные случаи посадки судна. 1. Основная плоскость (хОу) горизонтальна, плоскость мидель–шпангоута (yOz) и ДП (хО z) вертикальны. Судно сидит без крена (прямо) и на ровный киль (угол крена θ = 0 и угол дифферента ψ = 0) (рис.1.5). В этом случае посадка судна характеризуется лишь одним параметром - осадкой Т = Тм.
Рис. 1.5. Посадка судна прямо и на ровный киль
2. Плоскость мидель - шпангоута (yOz) вертикальна, ДП (хО z) наклонена на угол θ, основная линия, проходящая через прямолинейный участок киля, горизонтальна (рис.1.6). Судно считается сидящим на ровный киль, но с креном. Посадка характеризуется осадкой на миделе Тм, осадками на правом Тп и на левом Тл бортах, а также углом крена θ. При этом в полусвязанной сис-теме координаты точек правого борта равны х,
Рис. 1.6. Посадка судна на ровный киль с креном
3. Диаметральная плоскость (xOz) вертикальна, а плоскость мидель-шпангоута (уО z) наклонена. Основная линия, а также первоначальная ватерлиния В0Л0 (ее называют накрашенной) образуют с горизонтальной плоскостью угол дифферента ψ). Судно считается сидящим прямо, но с дифферентом и его посадка характеризуется осадкой Ти и углом ψ) (рис. 1.7).
Рис. 1.7. Посадка судна прямо с дифферентом
При малых дифферентах судно вращается так, что центр тяжести площади начальной ватерлинии F, лежащий на расстоянии
а на кормовом - Изменение осадки на носовом перпендикуляре можно определить, считая, что линия форштевня в пределах изменения осадки вертикальна. Из Δ FEA получим δТн = АЕ = FE tg ψ, или Соответственно из Δ FE 1 A 1 получим На основании формул (1.10) и (1.11) Тн = T + В выражения (1.10), (1.11) величины При проведении расчетов часто необходимо знать осадку на каком-либо шпангоуте, находящемся на расстоянии С помощью рис. 1.7 можно записать по аналогии с формулой (1.12) Т i = T + Для мидель - шпангоута x i = 0, и из выражения (1.14) следует T м = T – x f tg ψ. (1.15) Осадку носом и кормой и осадку на i -м шпангоуте можно выразить через осадку на мидель - шпангоуте, если выражение (1.15) подставить в формулы (1.12) и (1.13): Тн = T м + Разность между Тн и Т к называется линейным дифферентом Δ, равным Δ = Тн - Т к = L tg ψ. (1.17) Так как угол ψ положителен при наклонении на нос, то линейный дифферент будет также положительным, а при наклонении на корму - отрицательным.
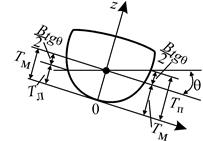
4. Плоскость мидель-шпангоута yOz наклонена, диаметральная плоскость xOz наклонена на угол
Рис. 1.8. Посадка судна с креном и дифферентом
В этом случае посадка определяется осадками на правом и левом борту В полусвязанной системе координат где Для решения некоторых задач статики требуется иметь уравнение плоскости ватерлинии в системе координат Oxyz. В общем случае это уравнение можно записать следующим образом: F (х, у, z) = Ах + By + Cz + D = 0. Если использовать параметры посадки В. Г. Власова, получим, что А = tg ψ; В = tg θ; С = -1; D = Тм, и уравнение плоскости ватерлинии окончательно запишется в виде: F (х, у, z) = x tg ψ + у tg θ - z + Тм = 0. В аналитической геометрии доказано, что угол α между плоскостью ватерлинии и ОП, равный углу между нормалью к плоскости ватерлинии и осью Oz, определяется из выражения После несложных выкладок получим откуда следует, что
|
||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 625; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.114.163 (0.008 с.) |

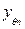 ,
, 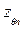 , а левого - х,
, а левого - х, 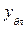 ,
, 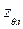 .
.

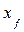 от плоскости мидель - шпангоута, остается неподвижным. Так как осадка в этом сечении равна Т, всоответствии с рис. 1.7 для осадки на носовом перпендикуляре можно записать
от плоскости мидель - шпангоута, остается неподвижным. Так как осадка в этом сечении равна Т, всоответствии с рис. 1.7 для осадки на носовом перпендикуляре можно записать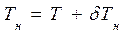 , (1.8)
, (1.8)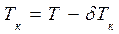 . (1.9)
. (1.9)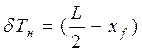 tg ψ. (1.10)
tg ψ. (1.10)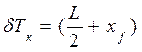 tg ψ . (1.11)
tg ψ . (1.11)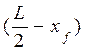 tg ψ; (1.12)
tg ψ; (1.12)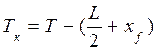 tg ψ. (1.13)
tg ψ. (1.13) и ψ подставляются со своими знаками.
и ψ подставляются со своими знаками.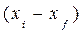 tg ψ. (1.14)
tg ψ. (1.14)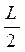 tg ψ;
tg ψ; 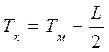 tg ψ; Т i = T м +
tg ψ; Т i = T м + 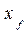 tg ψ. (1.16)
tg ψ. (1.16) . Первоначальная В0Л0 образует с горизонтальной плоскостью угол дифферента
. Первоначальная В0Л0 образует с горизонтальной плоскостью угол дифферента  (рис. 1.8). Считается, что судно сидит и с креном, и с дифферентом (общий случай посадки).
(рис. 1.8). Считается, что судно сидит и с креном, и с дифферентом (общий случай посадки). 
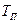 ,
, 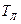 и осадками носом
и осадками носом 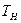 и кормой
и кормой 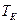 , причем
, причем 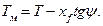
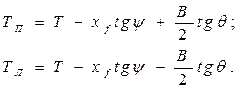 (1.18)
(1.18)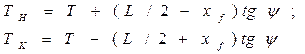 (1.19)
(1.19)  шпангоутное сечение накрененного судна можно рассматривать так же, как и в прямом положении и применять все формулы, выведенные при θ = 0. При этом осадка, отсчитываемая по оси
шпангоутное сечение накрененного судна можно рассматривать так же, как и в прямом положении и применять все формулы, выведенные при θ = 0. При этом осадка, отсчитываемая по оси 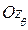 , в каждом сечении с абсциссой x i будет равна
, в каждом сечении с абсциссой x i будет равна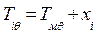 tg
tg 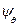 , (1.20)
, (1.20)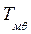 = Тм cos θ; tg
= Тм cos θ; tg 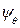 = tg ψ cos θ. Осадка
= tg ψ cos θ. Осадка 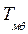 и дифферент
и дифферент 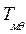 - осадка на мидель - шпангоуте, а угол между плоскостью действующей ватерлинии и плоскостью хОу представляет собой угол дифферента
- осадка на мидель - шпангоуте, а угол между плоскостью действующей ватерлинии и плоскостью хОу представляет собой угол дифферента 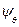 , значение которого положительно при дифференте на нос.
, значение которого положительно при дифференте на нос.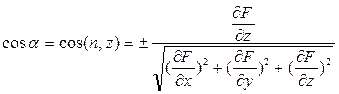 .
.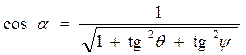 ,
, 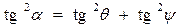 .
. 


