
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интерполяционные кривые остойчивости формыСодержание книги
Поиск на нашем сайте
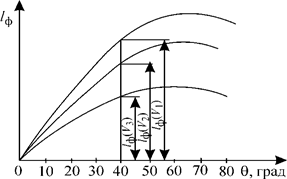
В процессе эксплуатации судно может плавать с различной нагрузкой, при этом оно будет иметь различные осадки и положение ЦТ. Чтобы не повторять громоздких расчетов остойчивости на больших углах крена для каждого случая нагрузки, применяются специальные интерполяционные кривые плеч остой-чивости формы. Если они заранее построены, то для любого необходимого нам водоизмещения V 0 можно снять l ф (10°), l ф (20°) и т.д., т.е. получить l ф (θ), а затем, зная положение ЦТ, в соответствии с п.3.3 рассчитать плечи статической остой-чивости по формуле Построение интерполяционных кривых производится с использованием зави-симостей l ф, рассчитанных для ряда водоизмещений, например, V 1, V 2, V 3, которые выбраны так, чтобы в интервале между V 1 и V 3 находились все возмож-ные в процессе эксплуатации водоизмещения (рис.3.18). Кривые перестраивают-ся в новых осях l ф и θ (рис.(3.17)). Сняв на рис.3.18 значения l ф (V 1), l ф (V 2) и l ф (V 3) для определенного угла крена, например, для угла 60°, откладывают их на рис.3.17 на вертикальной линии, соответствующей каждому значению водоизме-щения. Затем построения продолжают для 50°, 40° и т.д. и полученные точки соединяют плавными кривыми. При полном погружении судна (V = V п - водоизмещение полностью погру-женного судна) ватерлиния отсутствует, т.е. l ф = 0, что и отражено на рис.3.17. Вместо интерполяционных кривых плеч остойчивости формы можно по-строить интерполяционные кривые моментов остойчивости формы M ф = ρ gV l ф. Они изображены на рис.3.19. При V =0 моменты остойчивости формы также равны нулю, что иногда очень удобно, так как фактически мы имеем еще одну точку для построения интерполяционных кривых.
Рис.3.17. Интерполяционные кривые плеч остойчивости формы
Рис.3.18. Зависимости l ф (V) для ряда водоизмещений
Рис.3.19. Интерполяционные кривые моментов остойчивости формы
Необходимо отметить, что если два водоизмещения, для которых рассчиты-ваются интерполяционные кривые, близки, в интервале между ними кривые могут быть заменены прямыми линиями. Приближенный способ построения интерполяционных кривых был предложен В. Г. Власовым. Он основан на комбинации расчета l ф по способу А. Н. Крылова или А. Н. Крылова - Дарньи для одного характерного водоизмещения V 1 и по приближенным формулам, рассмотренным далее в п.3.9, для двух других водоизмещений V 2 = V п / 2 и V 3 = V п – V 1. Существует еще один вид интерполяционных кривых - пантокарены. Это кривые зависимости от водоизмещения плеч статической остойчивости Имея пантокарены, легко построить диаграмму статической остойчивости для расчетного случая нагрузки судна, вычисляя где
Рис.3.20. Пантокарены
3.9. Приближенные формулы для определения плеч остойчивости формы. Существует ряд приближенных формул для расчета плеч остойчивости формы (а следовательно, и плеч статической остойчивости), которые можно использовать в начальной стадии проектирования при отсутствии теоретического чертежа. При этом для определения необходимых в расчетах величин часто применяются статистические данные, полученные при обработке результатов расчетов для близких по форме и размерениям судов, или приближенные формулы для определения элементов плавучести, приведенные в п. 1.16, а также некоторые другие. Они даны ниже. Плечи остойчивости формы можно аппроксимировать в виде параболических или тригонометрических рядов. Наиболее распространено представление в виде рядов Фурье. Н.А. Заботкин предложил шестичленное разложение В этом разложении свободный член равен нулю и оставлены только синусы, так как плечи остойчивости формы – нечетные функции. Для коэффициентов выражения (3.45) получены формулы В выражениях (3.46) стоят координаты ЦВ и метацентрические радиусы, рассчитанные соответственно при 0 о, 90 о и 180 о. Если величины подводного и надводного водонепроницаемых объемов будут равны, т.е. V = V п / 2, получится, что r 180 = r 0 , z 180 =2 z 90 - zc, или иначе z 180 – z c= =2(z 90 - zc), и
Формула Н.А. Заботкина обращается в четырехчленную формулу В.Г. Власова Эту формулу можно применять и для других случаев загрузки судов, но она будет тем точнее, чем ближе по величине подводный и надводный водонепрони-цаемые объемы друг к другу, и будет иметь тем большую погрешность, чем величины объемов дальше друг от друга. От этого недостатка свободна четырехчленная формула, полученная из усло-вия равенства нулю двух последних коэффициентов где Существуют и четырехчленные формулы, полученные из других соображений, а также трехчленные формулы различных авторов.
|
||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 315; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.93.61 (0.006 с.) |

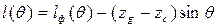 . (3.43)
. (3.43)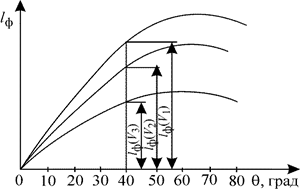
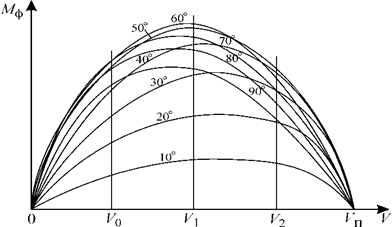
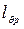 , отсчитываемых от Р - условного ЦТ, положение которого выбирают таким образом, чтобы во всем диапазоне углов крена (обычно от 10° до 90°) и водоизмещений плечи статической остойчивости оставались положительными. Чаще всего его располагают на ОП. При построении пантокарен необязательно проводить равнообъемные ватерлинии при нескольких водоизмещениях. В выбранном диапазоне водоизмещений (обычно от водоизмещения порожнего судна до водоизмещения судна с полным грузом) можно провести способом вращения или каким-либо иным способом кренование корпуса и непосредственно вычислить значения плеч статической остойчивости для углов θ = 10°, 20°,…, 90°. Они будут соответствовать разным водоизмещениям. По оси абсцисс откладывают водоизмещение, а по оси ординат - плечи статической остойчивости, рассчитанные относительно условного ЦТ. Каждое плечо следует откладывать соответственно водоизмещению, для которого оно вычислено. Соединив плавными кривыми точки, отвечающие одинаковым углам крена, получаем пантокарены для выбранного условного ЦТ, аппликата которого zg р указывается на чертеже пантокарен (рис.3.20). Ясно, что в отличие от интерполяционных кривых, для полностью погруженного судна пантокарены в общем случае в нуль не обращаются (они приходят к нулю только в том частном случае, когда условный ЦТ принят в ЦВ судна в прямом положении, т.е.
, отсчитываемых от Р - условного ЦТ, положение которого выбирают таким образом, чтобы во всем диапазоне углов крена (обычно от 10° до 90°) и водоизмещений плечи статической остойчивости оставались положительными. Чаще всего его располагают на ОП. При построении пантокарен необязательно проводить равнообъемные ватерлинии при нескольких водоизмещениях. В выбранном диапазоне водоизмещений (обычно от водоизмещения порожнего судна до водоизмещения судна с полным грузом) можно провести способом вращения или каким-либо иным способом кренование корпуса и непосредственно вычислить значения плеч статической остойчивости для углов θ = 10°, 20°,…, 90°. Они будут соответствовать разным водоизмещениям. По оси абсцисс откладывают водоизмещение, а по оси ординат - плечи статической остойчивости, рассчитанные относительно условного ЦТ. Каждое плечо следует откладывать соответственно водоизмещению, для которого оно вычислено. Соединив плавными кривыми точки, отвечающие одинаковым углам крена, получаем пантокарены для выбранного условного ЦТ, аппликата которого zg р указывается на чертеже пантокарен (рис.3.20). Ясно, что в отличие от интерполяционных кривых, для полностью погруженного судна пантокарены в общем случае в нуль не обращаются (они приходят к нулю только в том частном случае, когда условный ЦТ принят в ЦВ судна в прямом положении, т.е. 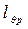 = l ф).
= l ф).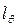 по формуле
по формуле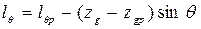 , (3.44)
, (3.44)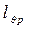 - плечо, снимаемое с пантокарен для расчетного водоизмещения судна; zg - аппликата ЦТ судна для расчетного случая нагрузки; zg р - аппликата услов-ного ЦТ).
- плечо, снимаемое с пантокарен для расчетного водоизмещения судна; zg - аппликата ЦТ судна для расчетного случая нагрузки; zg р - аппликата услов-ного ЦТ).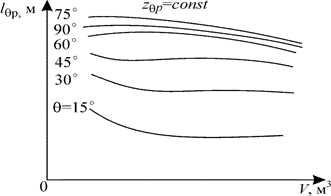
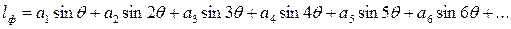 (3.45)
(3.45)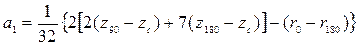 ;
;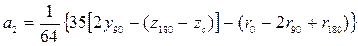 ;
;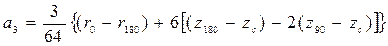 ;
; 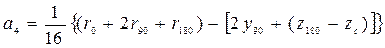 ;
;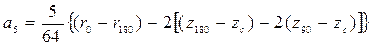 ;
;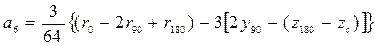 . (3.46)
. (3.46)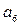 =
= 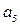 = 0. Таким образом, останется всего четыре члена ряда с коэффициентами
= 0. Таким образом, останется всего четыре члена ряда с коэффициентами 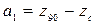 ;
; 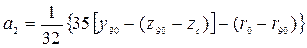 ;
;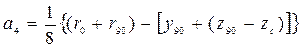 ;
;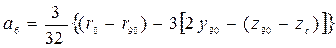 . (3.47)
. (3.47)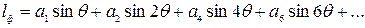 (3.48)
(3.48)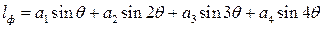 , (3.49)
, (3.49)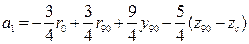 ;
; 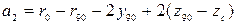 ;
;
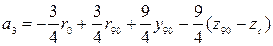 ;
;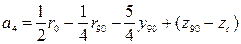 . (3.50)
. (3.50)


