
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Объемное водоизмещение и координаты ЦВ при посадке судна прямо и на ровный кильСодержание книги
Поиск на нашем сайте
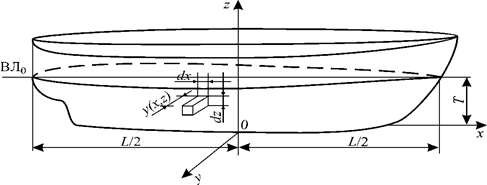
Объемное водоизмещение можно определить как погруженный объем корпуса судна. Для этого выделим сначала элементарный объем в виде опирающейся на ДП призмы со сторонами основания dx, dz и высотой у (х, z) (рис. 1.10): dV = у (х, z) dxdz. Проинтегрировав обе части этой формулы по всей ДП, получим объемное водоизмещение в следующем виде: Двойка перед интегралом учитывает симметрию корпуса относительно ДП. Порядок интегрирования может быть и обратным, т. е. Для судна, имеющего несимметрию погруженной части корпуса относительно ДП, объемное водоизмещение определяется как сумма объемов правой и левой частей корпуса: где yп ,, z п — координаты точек, лежащих на правой ветви шпангоута; yл, z л — то же на левой ветви шпангоута.
Рис. 1.10. К определению V В процессе расчетов статики корабля обычно заранее определяют площади ватерлиний и шпангоутов. Выведем формулы для вычисления объемного водоизмещения через эти элементы. Выделим двумя плоскостями, параллельными ОП, элементарный объем dV в виде слоя толщиной dz (рис. 1.11). В основании его лежит площадь ватерлинии S, и, так как в пределах dz судно можно считать прямобортным, dV = Sdz. Взяв интеграл в пределах осадки, получим формулу для определения водоизмещения Аналогичным образом выделим элементарный объем dV = Ω dx, где Ω - площадь погруженной части шпангоута. В этом случае при интегрировании по длине судна получаем Координаты ЦВнаходим из формул где Myz, M zх , Mxy — статические моменты погруженного объема относительно координатных плоскостей yOz, zOx, хОу соответственно. Так как в прямом положении погруженная часть корпуса судна симметрична относительно ДП (плоскости хОz), момент M zх =0 и ус = 0. Чтобы определить Myz, выпишем выражение для статического момента элементарного объема Ω dx; dMyz = Ω xdx, тогда
Рис. 1.11. К определению V с помощью Ω и S
Для хс можно получить еще одну формулу, которая оказывается отдельных случаях более удобной. Так как кроме S всегда известна абсцисса хf центра тяжести F площади ватерлинии, статический момент dMyz элементарного объема Sdz, можно определить по формуле dMyz = S х f dz, откуда Согласно выражению (1.34) абсцисса ЦВ равна Для нахождения М xy напишем выражение для статического момента элементарного объема Sdz: dMxy = Szdz. Тогда Для судов, имеющих несимметрию погруженной части корпуса относительно ДП, координаты ЦВ вычисляют по формулам (1.34).
|
||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 265; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.235.100 (0.009 с.) |

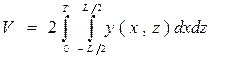 . (1.31)
. (1.31)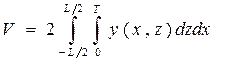 .
. 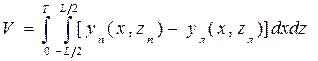 ,
, 
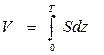 . (1.32)
. (1.32)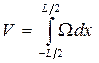 . (1.33)
. (1.33)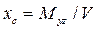 ;
; 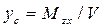 ;
; 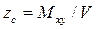 . (1.34)
. (1.34) 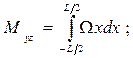
 . (1.35)
. (1.35)
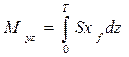 . (1.36)
. (1.36) 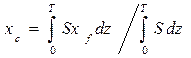 . (1.36а)
. (1.36а) 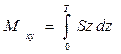 ;
; 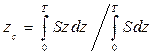 . (1.37)
. (1.37)  При расчетах элементов статики необходимо знать зависимости V (z), zc (z), xc (z), которые могут быть вычислены при помощи аналогичных интегралов, но с переменным верхним пределом:
При расчетах элементов статики необходимо знать зависимости V (z), zc (z), xc (z), которые могут быть вычислены при помощи аналогичных интегралов, но с переменным верхним пределом: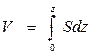 ;
; 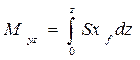 ;
; 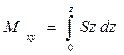 ; (1.38)
; (1.38)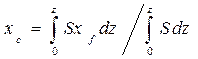 ;
; 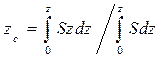 . (1.39)
. (1.39)


