
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Рекомендовано в качестве учебника дляСодержание книги
Поиск на нашем сайте
Р. В. БОРИСОВ
СТАТИКА КОРАБЛЯ Рекомендовано в качестве учебника для студентов вузов, обучающихся по направлению «Кораблестроение и морская системотехника»
Санкт-Петербург
2014 г.
Рецензенты Статика корабля: учебник Борисов Р. В.
В соответствии с программами курсов «Статика корабля» и «Теория корабля» рассмотрены плавучесть и остойчивость неповрежденного и аварийного судна, даны методы их расчета и принципы нормирования. Изложены принципиальные подходы к решению основных задач статики судна. Для студентов кораблестроительных ВУЗов и факультетов.
ПРЕДИСЛОВИЕ Настоящий учебник написан в соответствии с программами курсов «Статика корабля» и «Теория корабля», читаемых студентам кораблестроительных ВУЗов и факультетов по направлению «Кораблестроение и морская системотехника». При подготовке учебника использованы материалы фундаментальных учебников В. В. Семенова – Тян – Шанского [22], учебника «Статика корабля» [19] с участием В. В. Рождественского, В. В. Луговского, Б. В. Мирохина под редакцией автора, а также учебников ряда других авторов, материалы и правила Российского Морского Регистра Судоходства, исследования отечественных и зарубежных авторов, материалы проектов судов транспортного флота. В отличие от ранее изданных учебников по статике корабля в книге дается только теоретическое изложение вопросов статики. Предполагается, что расчетные примеры, алгоритмы и принципы расчетов на ЭВМ элементов статики будут изложены в отдельных внутривузовских изданиях с учетом особенностей частных методик, а также имеющегося в ВУЗах программного обеспечения. В свете современных требований Российского Морского Регистра Судоходства определенное место уделено вопросам нормирования остойчивости и непотопляемости морских судов.
Учебник состоит из введения и пяти глав.
ВВЕДЕНИЕ
Теория корабля (судна) - наука о его мореходных качества х: плавучести, остойчивости, непотопляемости, ходкости, умеренности качки и управляе-мости. Изучение и исследование мореходных качеств производится с учетом особенностей формы обводов корпуса, главных размерений корабля, распределения грузов и внешних нагрузок. Знание мореходных качеств необходимо при проектировании корабля, когда решается задача о выборе характеристик мореходных качеств, обеспечивающих надежную и безаварийную эксплуатацию корабля при различных режимах плавания, а также в процессе эксплуатации для их контроля и регулирования с целью обеспечения безопасности плавания.
В виду того, что корабль - твердое тело, наука о теории корабля опирается на законы теоретической механики, но поскольку движение его происходит в жидкости, требуется знание законов движения жидкости, т.е. гидромеханики, поэтому теорию корабля иногда называют гидромеханикой корабля. Рассмотрим основные определения мореходных качеств. Плавучесть - способность свободного корабля плавать в определенном положении относительно поверхности воды. Остойчивость - способность корабля, выведенного из положения равновесия внешним воздействием, возвращаться в положение равновесия после прекращения этого воздействия. В процессе эксплуатации корабля возможно возникновение аварийных ситуаций, при этом корабль должен сохранять в определенной мере плавучесть и остойчивость, т. е. обладать непотопляемостью (это не самостоятельное мореходное качество, а способность сохранять мореходные качества). Ходкость — способность корабля двигаться с заданной скоростью при эффективном использовании мощности силовой установки. Умеренность качки является следующим мореходным качеством. Качка – это колебательное движение корабля при перемещении его или стоянке на поверхности или под поверхностью воды. Качка – исключительно вредное явление. В понятие умеренность качки входят малость и плавность наклонений. Управляемость - способность корабля удерживать заданное направление движения или изменять его в соответствии с действиями судоводителя. Плавучесть, остойчивость, а также непотопляемость объединяются в раздел, называемый статикой корабля; ходкость, качка и управляемость — в раздел, именуемый динамикой корабля, Указанное выше разделение мореходных качеств носит условный характер. В реальных условиях при движении в море корабль подвержен действию волн и ветра, поэтому рассмотрение плавучести и остойчивости необходимо производить с учетом параметров его качки. С другой стороны, обеспечение плавности качки определенным образом связано с направлением движения корабля, характеристиками волн, параметрами движителей и рулей, а также различных успокоителей качки, т.е. качка, ходкость и управляемость должны рассматриваться вместе.
Настоящий учебник посвящен рассмотрению статики, т. е. плавучести, остойчивости и непотопляемости корабля. Учение о плавучести и остойчивости основывается на законе Архимеда, который сводится к следующему: «На всякое тело, погруженное в жидкость, действует со стороны этой жидкости поддерживающая сила, равная силе тяжести вытесненной телом жидкости, направленная вверх и проходящая через центр тяжести вытесненного объема». Поддерживающую силу, действующую на погруженную часть корабля, называют Архимедовой силой. Закон Архимеда был открыт в III в. до н. э., но практическое применение его началось лишь в XVII в., когда впервые в 1666 г. английский инженер А. Дин предсказал осадку военного корабля «Рупперт», что дало возможность до его спуска прорезать в бортах порты для пушек. В XVIII в. в России и во Франции практически одновременно появились два сочинения, в которых впервые излагались вопросы теории корабля. В 1746 г. издано в Париже членом Французской академии наук П. Бугером сочинение «Трактат о корабле, его конструкции и о движении». В 1749 г. член Российской академии наук Л. Эйлер опубликовал в Петербурге сочинение «Корабельная наука». В этих трудах было изложено учение о плавучести, сформулировано понятие о метацентре и метацентрической высоте, развито учение о сопротивлении жидкости движению судов, решен целый ряд вопросов, относящихся к мореходным качествам кораблей. Разработка вопросов статики продолжалась во второй половине XVIII в. и в первой половине XIX в. Были выработаны практические приемы расчета элементов плавучести и начальной остойчивости по теоретическому чертежу, методы определения положения центра тяжести корабля. Английский корабельный инженер Э. Рид во второй половине XIX в. считал недостаточным вычисление только начальной остойчивости и предложил рассматривать характеристики остойчивости парусных бронированных военных кораблей при больших углах наклонений. Внедрение этого предложения в практику кораблестроения началось лишь после гибели в результате действия шквала одного из военных кораблей английской эскадры в 1870 г. Примерно к этому же времени относится переход к применению в статике корабля методов приближенных вычислений. К началу XX в. появились снаряды и мины, вызывающие большие пробоины в корпусе корабля, а иногда его затопление и гибель. Возникла необходимость в разработке нового раздела статики - непотопляемости. Учение о непотопляемости создано русскими учеными С. О. Макаровым, А. Н. Крыловым и И. Г. Бубновым. Известный русский ученый и флотоводец адмирал С. О. Макаров на основе анализа аварий и гибели ряда кораблей русского военного флота сформулировал требования к непотопляемости военных кораблей. Идеи С. О. Макарова А. Н. Крылов теоретически развил и воплотил в инженерную практику. В русском кораблестроении были введены предложенные А. Н. Крыловым «Таблицы непотопляемости»; за границей они были введены значительно позже.
В связи с непотопляемостью необходимо также упомянуть имена И. Г. Бубнова и Р. А. Матросова. И. Г. Бубнов исследовал зависимость характеристик непотопляемости корабля от подразделения его корпуса на водонепроницаемые отсеки. Р. А. Матросов впервые выполнил анализ остойчивости поврежденного корабля при больших наклонениях. Ученики и последователи А. Н. Крылова и И. Г. Бубнова успешно развивали теоретические положения и инженерные методы расчета непотопляемости применительно к кораблям различных типов. Особенно много в этой области сделали Ю. А. Шиманский, В. Г. Власов, В. В. Семенов – Тян - Шанский, С. Н. Благовещенский, Д. В. Дорогостайский, Н. Я. Мальцев, Н. П. Муру. В связи с ростом в последние десятилетия тоннажа, числа и типов судов мирового транспортного флота, возросло количеств аварий в процессе эксплуатации судов, поэтому классификационные общества повысили требования к мореходным качествам судов и в том числе к плаву-чести и остойчивости неповрежденного и поврежденного судов. Большое развитие получили исследования по нормированию остойчивости и непотопляемости судов транспортного флота. Большой вклад в эти исследования внесли С. Н. Благовещенский, В. В. Луговский и другие ученые. В. В. Луговский исследовал теоретические основы нормирования остойчивости, Н. Б. Севастьянов разработал предложения по нормированию остойчивости судов промыслового флота. В. Н. Волков, В. С. Дорин и В. Ф. Мейлунас предложили вероятностные оценки непотопляемости морских транспортных судов. Большинство основных расчетов по статике корабля раньше производили приближенными методами в табличной форме с помощью логарифмической линейки и арифмометра. Для выполнения всего необходимого комплекса расчетов элементов статики требовалось большое количество времени. В настоящее время расчеты статики выполняются на ЭВМ. Большой вклад в разработку алгоритмов, программ и методик расчетов элементов статики на ЭВМ внесли М. Н. Рейнов и В. И. Брегман. В 60-х гг. нашего столетия они положили начало этим исследованиям. Алгоритмы и программы расчетов статики корабля, разработанные под руководством М. Н. Рейнова, вошли в первую отечественную систему автоматического проектирования судов и используются во всех центральных конструкторских бюро.
Для обеспечения надежной эксплуатации морских транспортных судов результаты расчетов элементов плавучести, остойчивости и непотопляемости находятся в распоряжении капитана судна. Если ранее эти данные представляли в виде чертежей и таблиц, то в последнее время разработаны программные комплексы для расчета на бортовых ЭВМ допустимых характеристик плавучести, остойчивости и непотопляемости при различных состояниях нагрузки судна. Большие работы в этом направлении были проведены в ЦНИИ Морского флота под руководством В.Б. Липиса.
Глава 1. ПЛАВУЧЕСТЬ Элементы площади ватерлинии Чтобы определить V, хс , zс ,необходимо знать площади ватерлиний S и абсциссы хf центров тяжести этих площадей. Для расчета остойчивости следует вычислить моменты инерции площадей ватерлиний относительно координатных осей Ох, Оу и оси ff, проходящей через центр тяжести площади ватерлинии. Вначале найдем элементы площади ватерлинии для судна, сидящего прямо и на ровный киль. Выделим элементарную площадь, (рис. 1.18) длиной dx и шириной 2у: dS = 2 ydx, тогда
Рис. 1.18. К определению элементов площади симметричной ватерлинии
Абсцисса ЦТ площади ватерлинии равна х f = My / S, (1.49) где My — статический момент площади ватерлинии относительно оси Оу. Для определения Му выпишем сначала выражение для статического момента элементарной площади dS: dMy = xdS = x 2 ydx, откуда Получим формулы для определения осевых моментов инерции площади ватерлинии относительно главных центральных осей, одной из которых является ось Ох (в силу симметрии ватерлинии относительно Ох), другой — ось ff, параллельная оси Оу и проходящая через точку F — центр тяжести площади ватерлинии. Найдем момент инерции dIx элементарной площади dS,для чего воспользуемся известной из теоретической механики формулой для момента инерции площади прямоугольника относительно главной центральной оси: тогда Момент инерции площади ватерлинии S относительно оси равен 1у - момент инерции площади ватерлинии относительно оси Оу, определенный по формуле В процессе эксплуатации судно может плавать с начальным креном, когда ватерлиния несимметрична относительно ДП. Чтобы рассчитать для данного случая площадь, статические моменты, моменты инерции и другие элементы, надо несколько изменить формулы (1.36)— (1.43). С этой целью введем правые уп и левые ул ординаты (рис. 1.19).
Согласно рис. 1.19 выражение для площади элемента с учетом того, что ул отрицательна, можно записать в виде dS = yn dx — ул dx =(уп - ул) dx, а пло-щадь ватерлинии как
Рис. 1.19. К определению элементов площади несимметричной ватерлинии
Аналогично для статического момента площади S относительно оси Оу получим Тогда Для несимметричной ватерлинии статический момент площади относительно оси Ох не равен нулю. Статический момент для правой элементарной площадки равен для левой –
суммарный - Тогда формула для полного статического момента запишется в виде Центр тяжести F площади ватерлинии будет находиться от ДП на расстоянии Для моментов инерции элементарной площадки можно записать следующие выражения: Следовательно, моменты инерции относительно осей координат будут равны Но в дальнейших расчетах нам потребуются моменты инерции относительно осей, проходящих через ЦТ F площади ватерлинии. Они определяются с учетом соответствующих переносных моментов инерции по формулам Формулы (1.54) - (1.61) имеют более общий характер, чем соответствующие формулы, полученные для симметричного судна. Для него уп = - ул ивыражения (1.54) - (1.61) переходят в (1.46) - (1.53). Формула (1.57) позволяет вычислить также статический момент погруженного объема М xz несимметричного судна относительно ДП, а затем и ординату ЦВ ус. Статический момент может быть представлен как интегральная сумма статических моментов элементарных объемов или с учетом (1.57) Ордината ЦВ Необходимо отметить, что использование формул (1.54) - (1.62) предполагает незначительную несимметрию относительно ДП, поэтому можно пре-небречь центробежным моментом инерции, т.е. I xy При вычислениях элементов площади ватерлиний многокорпусных плавучих объектов (плавучие буровые установки, трисеки и т.д.) используются два основных метода, применение каждого из которых зависит от особенностей формы площадок, составляющих ватерлинию. Если ватерлиния состоит из площадок сложной формы, в том числе и характерной для ватерлиний обычных судов (например, рис. 1.20), можно использовать подход, продемонстрированный при выводе формул (1.54) - (1.62). Тогда получим: S = Mx =
My = I x = Iy = Величины xf , yf , I xf и Iyf определяются по формулам (1.56), (1.58) и (1.61). При большом числе корпусов формулы (1.63) - (1.67) можно обобщить. Тогда получим: S = Mx = My = Ix = Iy = Здесь m - число правых ординат, k – текущий номер правой ординаты, n - число левых ординат, l – текущий номер левой ординаты. Величины xf , yf , Ixf и Iyf определяются по формулам (1.56), (1.58) и (1.61).
Рис. 1.20. К определению элементов площади ватерлинии, состоящей из площадок сложной формы
Если же ватерлиния состоит из площадок простой формы (круг, эллипс, прямоугольник и т.д.), для которых можно заранее рассчитать характеристики площади относительно собственных центральных осей (sk - площадь, ixk - момент инерции площади относительно собственной центральной оси Ok ¢ хk ¢, параллельной главной оси Ox; iyk - момент инерции площади относительно собственной центральной оси Ok ¢ уk ¢, параллельной главной центральной оси Oy (см. рис. 1.21), то получатся следующие формулы: S = My = где n - число площадок, составляющих площадь ватерлинии. Здесь также предполагается, что центробежный момент инерции Ixy = 0. Величины xf , yf , Ixf , Iyf определяются по формулам (1.56), (1.58) и (1.61).
Рис. 1.21. К определению элементов площади ватерлинии, состоящей из площадок простой формы
Перенос груза Пусть на судне некоторый груз p массой m перенесен так, что ЦТ этого груза переместился из точки с координатами x 0, y 0, z 0 в точку с координатами x 1, y 1, z 1. Тогда масса всего судна не изменится, но изменится положение его ЦТ. Раскладывая фактическое перемещение ЦТ груза на три взаимно перпен-дикулярных перемещения, параллельные координатным осям, рассматриваем продольное перемещение l x = x 1— x 0, поперечное перемещение l у = y 1 — y 0 и вертикальное перемещение lz = z 1 — z 0 (рис. 2.14). Исследование одновременного воздействия всех трех перемещений на посадку и остойчивость судна приводит к сложным выкладкам, поэтому вначале разберем перенос груза по вертикали на расстояние lz, а затем перенос груза в горизонтальной плоскости на расстояния l у и l х. Перенос груза по вертикали. Перемещение ЦТ судна можно найти с помощью теоремы теоретической механики о статических моментах, согласно которой
Рис. 2.14. Наклонение судна при переносе малого груза в поперечной плоскости
Согласно (2.17) и (2.21) метацентрические высоты равны
Для приращений метацентрических высот по аналогии можно записать
Однако при вертикальном переносе груза изменения водоизмещения, осадки и формы подводной части судна нет, поэтому первые два слагаемых в каждой из формул (2.29) равны нулю. Таким образом, изменения метацентрических высот будут одинаковы Подставляя в эту формулу выражение (2.28), получим Если груз переносится вниз, то Если же груз переносят вверх, то Для большинства судов продольная метацентрическая высота намного больше поперечной. Поэтому в практических расчетах поправкой Таким образом, новые метацентрические высоты будут равны Восстанавливающие моменты будут соответственно равны Перенос груза по горизонтали. При переносе груза по оси Оу на расстояние l у возникает кренящий момент Из этой формулы можно получить угол крена, с которым будет плавать судно В случае переноса груза на правый борт При переносе груза по оси Ох возникает дифферентующий момент Если груз переносится в нос, то где положительные значения
Рис. 2.15. Определение осадок носом и кормой при приеме малого груза
Если
Прием и расходование груза Расчетные оценки изменения посадки и остойчивости судна при приеме и расходовании грузов существенно различаются для относительно малого и относительно большого грузов. В первом случае можно получить достаточно простые расчетные формулы, во втором пользуются графическими зависимостями. Напоминаем, что решение вопроса о том, какой груз следует считать относительно малым, а какой большим, зависит от формы обводов судна в районе изменения осадки. Чем больше протяженность вертикальных бортов в этом районе, тем выше пределы применимости формул для приема малого груза. Как правило, груз считается относительно малым, если вес его не превышает (5—10) % от веса судна D. Прием и расходование относительно малого груза. Предположим, что на судно принят относительно малый груз p. Обозначим через xp, yp, zp координаты ЦТ принятого груза. В результате приема груза изменятся средняя осадка и остойчивость, могут возникнуть крен и дифферент судна. Для упрощения вывода расчетных формул разобьем рассматриваемую операцию на две части. Сначала примем груз таким образом, чтобы не возникало ни крена, ни дифферента. Эта задача нами уже решалась в п. 1.14.1. Затем перенесем в горизонтальной плоскости груз в место его фактического приема. При этом могут появиться крен и дифферент. Как следует из п.1.14.1, чтобы при приеме малого груза не возникало крена и дифферента, ЦТ груза должен располагаться на одной вертикали с ЦТ площади ватерлинии. Поэтому примем вначале груз в точку с координатами x f, 0, zp, где аппликата z p может быть любой. Изменение средней осадки определится формулой (1.93) Найдем изменение поперечной метацентрической высоты. В соответствии с первой формулой (2.29) Изменение аппликаты ЦТ судна определяется формулой (1.97) а изменение аппликаты ЦВ - формулой (1.100) Изменение поперечного метацентрического радиуса равно Подставляя значения Отсюда поперечная метацентрическая высота после приема груза равна Аналогичным путем определяется изменение продольной метацентрической высоты Изменение продольного метацентрического радиуса находим аналогично (2.42), считая судно прямобортным После подстановки значений Для большинства судов величина Тогда продольная метацентрическая высота после приема груза будет равна В случае расходования груза величину p следует вводить в формулы (2.42) и (2.46) со знаком минус. Найдем изменение коэффициентов остойчивости, входящих в выражения (2.14а) и (2.15). Умножая (2.42) и (2.47) на величину и для коэффициента продольной остойчивости Следовательно, для боль
|
|||||||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 256; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.37.242 (0.017 с.) |

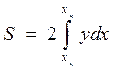 . (1.48)
. (1.48)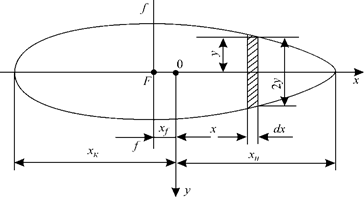
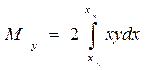 . (1.50)
. (1.50)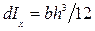 , где b = dx, h = 2 y, т. e.
, где b = dx, h = 2 y, т. e.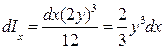 ,
,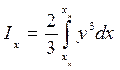 . (1.51)
. (1.51)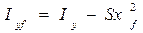 , (1.52)
, (1.52)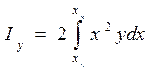 , (1.53) так как элементарный момент инерции площади dS равен
, (1.53) так как элементарный момент инерции площади dS равен 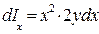 .
. 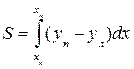 . (1.54)
. (1.54)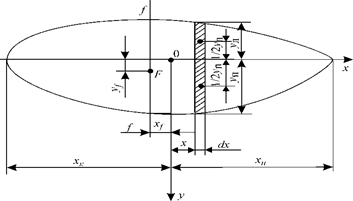
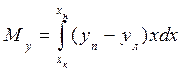 . (1.55)
. (1.55)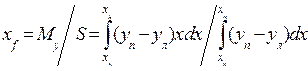 . (1.56)
. (1.56)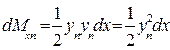 ,
,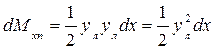 ,
,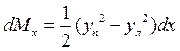 .
.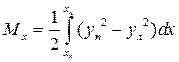 . (1.57)
. (1.57)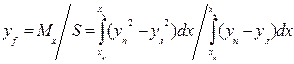 . (1.58)
. (1.58)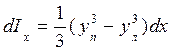 ;
; 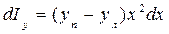 .
.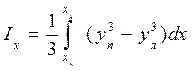 ; (1.59)
; (1.59)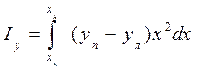 . (1.60)
. (1.60)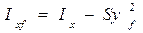 ;
;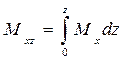 ,
,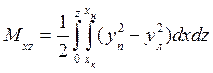 .
.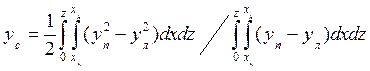 . (1.62)
. (1.62)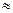 0.
0.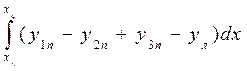 ; (1.63)
; (1.63)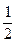
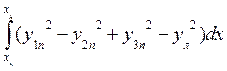 ; (1.64)
; (1.64)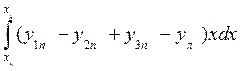 (1.65)
(1.65)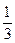
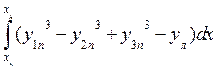 ; (1.66)
; (1.66)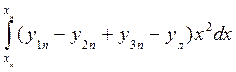 . (1.67)
. (1.67)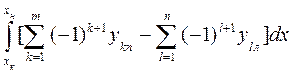 ; (1.68)
; (1.68)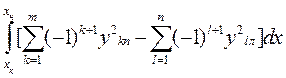 ; (1.69)
; (1.69)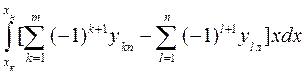 ; (1.70)
; (1.70)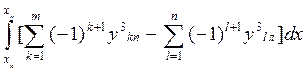 ; (1.71)
; (1.71)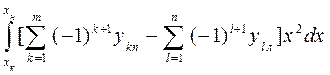 . (1.72)
. (1.72)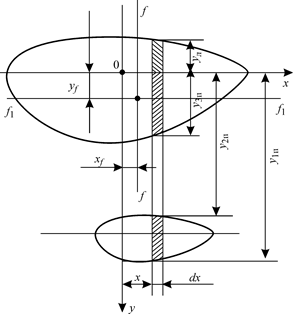
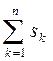 ; Ix =
; Ix = 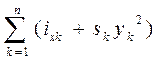 ; Iy =
; Iy = 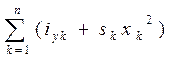 ;
; 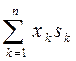 ; Mx =
; Mx = 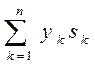 , (1.73)
, (1.73) 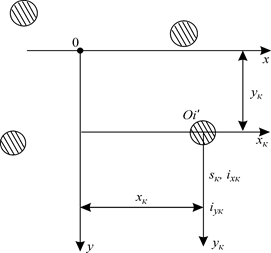
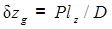 . (2.28)
. (2.28)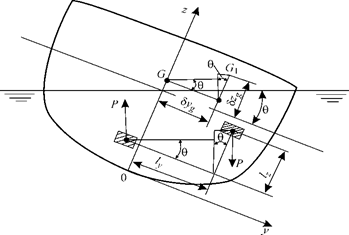
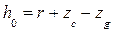 ;
;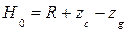 .
.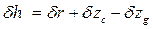 ;
;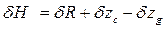 . (2.29)
. (2.29)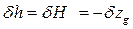 . (2.30)
. (2.30)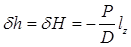 , (2.31)
, (2.31)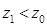 ,
, 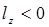 и согласно формуле (2.31)
и согласно формуле (2.31) 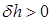 , т. е. начальная остойчивость увеличивается.
, т. е. начальная остойчивость увеличивается.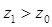 ,
, 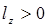 и
и 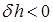 , т. е. начальная остойчивость снижается. Очевидно, возможен случай, когда при переносе грузов вверх поперечная метацентрическая высота станет равной нулю или даже отрицательной. На практике таких случаев следует избегать, поскольку они запрещены правилами безопасной эксплуатации судов.
, т. е. начальная остойчивость снижается. Очевидно, возможен случай, когда при переносе грузов вверх поперечная метацентрическая высота станет равной нулю или даже отрицательной. На практике таких случаев следует избегать, поскольку они запрещены правилами безопасной эксплуатации судов.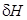 почти всегда можно пренебречь по сравнению с
почти всегда можно пренебречь по сравнению с 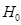 .
.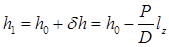 ;
;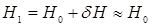 . (2.32)
. (2.32)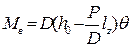 ; (2.33)
; (2.33)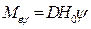 . (2.34)
. (2.34)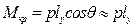 . Статическое равновесие наступает при равенстве кренящего и восстанавливающего моментов
. Статическое равновесие наступает при равенстве кренящего и восстанавливающего моментов 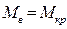 , или с учетом (2.33)
, или с учетом (2.33)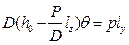 . (2.35)
. (2.35)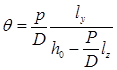 . (2.36)
. (2.36) 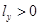 и
и 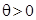 , а в случае переноса на левый
, а в случае переноса на левый 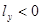 и
и 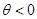 .
.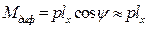 и все рассуждения относительно равенства дифферентующего и восстанавливающего моментов можно повторить. Окончательно получим угол дифферента
и все рассуждения относительно равенства дифферентующего и восстанавливающего моментов можно повторить. Окончательно получим угол дифферента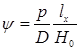 . (2.37)
. (2.37) 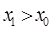 ,
, 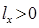 , а значит и
, а значит и 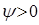 , т. е. судно получает дифферент на нос. Если же груз переносится в корму, то
, т. е. судно получает дифферент на нос. Если же груз переносится в корму, то 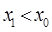 ,
, 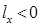 ,
, 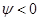 , т. е. судно дифферентуется на корму. Изменение осадок носом и кормой можно определить, используя теорему Эйлера. Проведем через точку F — ЦТ площади ватерлинии В0Л0 судна в прямом положении — наклонную ватерлинию В
, т. е. судно дифферентуется на корму. Изменение осадок носом и кормой можно определить, используя теорему Эйлера. Проведем через точку F — ЦТ площади ватерлинии В0Л0 судна в прямом положении — наклонную ватерлинию В 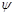 Л
Л 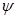 (рис. 2.15). Тогда для изменения осадок носом
(рис. 2.15). Тогда для изменения осадок носом 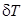 и кормой
и кормой 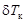 можно записать:
можно записать: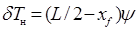 ;
; 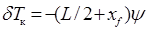 , (2.38)
, (2.38)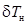 и
и 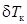 соответствуют увеличению осадок носом T н и кормой T к, а отрицательные – их уменьшению. Дифферент (в метрах) определяется выражением:
соответствуют увеличению осадок носом T н и кормой T к, а отрицательные – их уменьшению. Дифферент (в метрах) определяется выражением: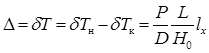 . (2.39)
. (2.39)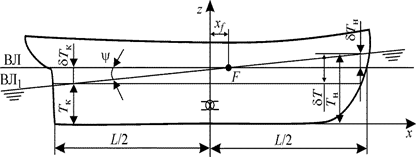
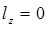 , т.е. груз переносится только по горизонтали
, т.е. груз переносится только по горизонтали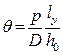 ; (2.36’)
; (2.36’)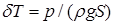 .
.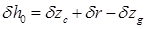 .
. 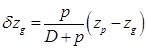 ,
,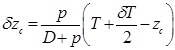 .
.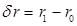 , где
, где 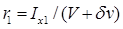 — метацентрический радиус после приема груза;
— метацентрический радиус после приема груза; 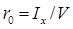 — метацентрический радиус до его приема. В формулах для r 1 и r 0 величина
— метацентрический радиус до его приема. В формулах для r 1 и r 0 величина 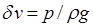 , а I x 1, и I x — моменты инерции площади ватерлинии после и до приема груза соответственно. Поскольку принятый груз полагаем малым и борта судна в пределах изменения осадки считаются вертикальными, площадь действующей ватерлинии неизменна и, следовательно,
, а I x 1, и I x — моменты инерции площади ватерлинии после и до приема груза соответственно. Поскольку принятый груз полагаем малым и борта судна в пределах изменения осадки считаются вертикальными, площадь действующей ватерлинии неизменна и, следовательно, 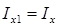 . Тогда после несложных преобразований получится
. Тогда после несложных преобразований получится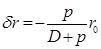 . (2.40)
. (2.40)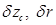 и
и 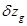 из формул (1.97), (1.100) и (2.40) в (2.39) с учетом выражения для
из формул (1.97), (1.100) и (2.40) в (2.39) с учетом выражения для 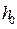 найдем
найдем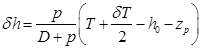 . (2.41)
. (2.41)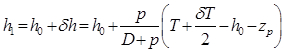 . (2.42)
. (2.42)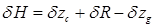 .
. 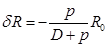 . (2.43)
. (2.43)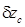 ,
, 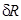 и
и 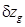 согласно формулам (1.97), (1.100) и (2.43) в
согласно формулам (1.97), (1.100) и (2.43) в 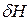 и несложных преобразований получим
и несложных преобразований получим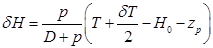 . (2.44)
. (2.44)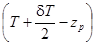 намного меньше H 0. Поэтому приближенно можно положить
намного меньше H 0. Поэтому приближенно можно положить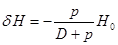 . (2.45)
. (2.45)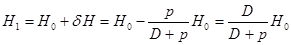 . (2.46)
. (2.46)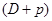 , получим для коэффициента поперечной остойчивости
, получим для коэффициента поперечной остойчивости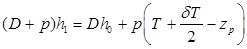 . (2.47)
. (2.47)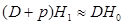 . (2.48)
. (2.48)


