Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Силы, действующие на плавающее судно. Условия равновесия суднаСодержание книги
Поиск на нашем сайте
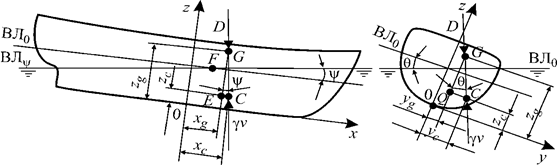
Плавающее судно может находиться в полупогруженном или полностью погруженном состоянии. Считается, что оно не совершает никаких движений, или совершает их настолько медленно, что можно пренебречь силами инерции корпуса и силами гидродинамической природы (инерцией окружающей воды, сопротивлением воды и т. д.). Плавающее судно будет находиться под действием сил тяжести всех частей судна и грузов, сил гидростатического давления на смоченную поверхность судна и сил аэростатического давления на поверхность частей судна и грузов, находящихся в воздухе. Поскольку судно рассматривается как абсолютно твердое тело, все эти распределенные силы можно заменить равнодействующими, проходящими через соответствующие точки. Судно будет находиться в равновесии в том случае, если сумма всех равнодействующих и сумма их моментов будут равны нулю. Силы тяжести всех частей корпуса и грузов приводятся к одной равнодействующей - силе тяжести судна D,направленной вертикально вниз и проходящей через центр тяжести (ЦТ) судна G. Его положение в связанной с судном системе координат определяется координатами xg, yg, zg. Сила тяжести связана с массой судна М формулой D = Mg, где g — ускорение свободного падения. Со стороны воды на каждый элемент смоченной поверхности судна будет действовать по нормали гидростатическое давление р = ρ g (T — z) + p 0 . (1.21) В этой формуле ρ - плотность воды; z - аппликата рассматриваемого элемента смоченной поверхности; р0 – атмосферное или аэростатическое давление. Аэростическое давление можно легко учесть, если считать, что на каждый элемент смоченной поверхности будет действовать только избыточное давление, т. е. р— p 0 = ρ g (T — z). Согласно закону Архимеда силы избыточного давления приведутся к равнодействующей где Ввиду того, что горизонтальные составляющие давлений с разных сторон корпуса уравновешивают друг друга, равнодействующая будет направлена вертикально вверх и по величине равна силе тяжести воды в объеме погруженной части судна, т. е. ρ gV. Сила ρ gV называется силой плавучести, объем погруженной части судна V - объемным водоизмещением, а величина М = ρ V - водоизмещением (массой). Сила плавучести проходит через центр тяжести С погруженного объема с координатами хс , ус , zc. Центр тяжести погруженного объема судна называется центром величины (ЦВ).
Рис. 1.9. Равновесие судна при произвольной посадке
Чтобы судно находилось в равновесии, сила плавучести должна быть равна силе тяжести судна, а ЦВ должен находиться на одной вертикали с ЦТ. Так как сила плавучести направлена вертикально вверх, а сила тяжести судна вертикально вниз, то главный вектор и главный момент всех сил, действующих на судно в положении равновесия, обращаются в нули. Первое условие равновесия запишется в виде D = ρ gV, (1.23) D = γ V, (1.23a) где γ = ρ g – удельный вес воды.Это уравнение называется уравнением плавучести. Из него, в частности, следует, что масса судна равна водоизмещению: М = D / g = ρ V. В уравнении (1.23), как мы видим, не учтена сила тяжести воздуха внутри корпуса. Это оправдано при решении практических задач, так как она составляет десятые доли процента от силы тяжести корпуса судна. Второе условие равновесия распадается на два. Согласно рис.1.9 при продольных наклонениях судна на угол ψ из Δ G E C следует, что xc —xg = (zg—zc) tg ψ. (1.24) При наклонении судна на угол θ из Δ GQC получается, что QC = QG tg θ, yc - yg = (zg - zc } tg θ. (1.25) Рассмотрим различные случаи посадки судна. 1. Судно сидит прямо (θ = 0), но с углом дифферента ψ. Тогда xc — xg = (zg — zc) tg ψ; yc – yg = 0, или yc = yg. (1.26) Так как у большинства судов корпус симметричен относительно ДП, 2. Судно сидит на ровный киль (ψ =0), но с углом крена θ. Тогда т. е. xc = xg; yc —yg = (zg—zc) tg θ. (1.27) 3. Судно сидит прямо (θ =0) и на ровный киль (ψ= 0). В этом случае xc = x g; yc = yg. (1.28) Для судна, симметричного относительно ДП, ус = yg = 0. Так как обычно углы дифферента малы, можно в пределах общей точности расчетов и в первом случае посадки использовать уравнения равновесия (1.28).
|
||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 210; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.118.214 (0.007 с.) |

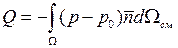 , (1.22)
, (1.22)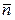 - внешняя нормаль к элементу смоченной поверхности;
- внешняя нормаль к элементу смоченной поверхности; 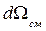 - элемент смоченной поверхности.
- элемент смоченной поверхности.