
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Составляющие восстанавливающего момента. Остойчивость формы и остойчивость весаСодержание книги
Поиск на нашем сайте
Подставим в формулу (2.14а) значение начальной метацентрической высоты Первая составляющая называется моментом остойчивости формы, так как поперечный метацентрический радиус зависит только от формы корпуса, а вторая составляющая - моментом остойчивости веса так как Тогда Проиллюстрируем выражение (2.27) соответствующим графическим примером (рис.2.13). Приложив условно в точке С 0 две взаимно уравновешивающиеся силы d, получим один момент с плечом
Рис.2.13. Составляющие восстанавливающего момента Изменение посадки и остойчивости судна при переносе, приеме и расхо-довании груза. Понятие о нейтральной плоскости. Метацентрическая диа-грамма Перенос, прием и расходование грузов являются повседневными операциями в процессе эксплуатации судна. Такие операции приводят к изменению посадки (средней осадки, углов крена и дифферента) и остойчивости судна. Как правило, это изменение с достаточной для практики точностью можно оценить по формулам начальной остойчивости. Пересчет диаграмм статической и динамической остойчивости проводят лишь в случаях, связанных главным образом с обеспечением безопасности плавания.
Перенос груза Пусть на судне некоторый груз p массой m перенесен так, что ЦТ этого груза переместился из точки с координатами x 0, y 0, z 0 в точку с координатами x 1, y 1, z 1. Тогда масса всего судна не изменится, но изменится положение его ЦТ. Раскладывая фактическое перемещение ЦТ груза на три взаимно перпен-дикулярных перемещения, параллельные координатным осям, рассматриваем продольное перемещение l x = x 1— x 0, поперечное перемещение l у = y 1 — y 0 и вертикальное перемещение lz = z 1 — z 0 (рис. 2.14). Исследование одновременного воздействия всех трех перемещений на посадку и остойчивость судна приводит к сложным выкладкам, поэтому вначале разберем перенос груза по вертикали на расстояние lz, а затем перенос груза в горизонтальной плоскости на расстояния l у и l х. Перенос груза по вертикали. Перемещение ЦТ судна можно найти с помощью теоремы теоретической механики о статических моментах, согласно которой
Рис. 2.14. Наклонение судна при переносе малого груза в поперечной плоскости
Согласно (2.17) и (2.21) метацентрические высоты равны
Для приращений метацентрических высот по аналогии можно записать
Однако при вертикальном переносе груза изменения водоизмещения, осадки и формы подводной части судна нет, поэтому первые два слагаемых в каждой из формул (2.29) равны нулю. Таким образом, изменения метацентрических высот будут одинаковы Подставляя в эту формулу выражение (2.28), получим Если груз переносится вниз, то Если же груз переносят вверх, то Для большинства судов продольная метацентрическая высота намного больше поперечной. Поэтому в практических расчетах поправкой Таким образом, новые метацентрические высоты будут равны Восстанавливающие моменты будут соответственно равны Перенос груза по горизонтали. При переносе груза по оси Оу на расстояние l у возникает кренящий момент Из этой формулы можно получить угол крена, с которым будет плавать судно В случае переноса груза на правый борт При переносе груза по оси Ох возникает дифферентующий момент Если груз переносится в нос, то где положительные значения
Рис. 2.15. Определение осадок носом и кормой при приеме малого груза
Если
Прием и расходование груза Расчетные оценки изменения посадки и остойчивости судна при приеме и расходовании грузов существенно различаются для относительно малого и относительно большого грузов. В первом случае можно получить достаточно простые расчетные формулы, во втором пользуются графическими зависимостями. Напоминаем, что решение вопроса о том, какой груз следует считать относительно малым, а какой большим, зависит от формы обводов судна в районе изменения осадки. Чем больше протяженность вертикальных бортов в этом районе, тем выше пределы применимости формул для приема малого груза. Как правило, груз считается относительно малым, если вес его не превышает (5—10) % от веса судна D. Прием и расходование относительно малого груза. Предположим, что на судно принят относительно малый груз p. Обозначим через xp, yp, zp координаты ЦТ принятого груза. В результате приема груза изменятся средняя осадка и остойчивость, могут возникнуть крен и дифферент судна. Для упрощения вывода расчетных формул разобьем рассматриваемую операцию на две части. Сначала примем груз таким образом, чтобы не возникало ни крена, ни дифферента. Эта задача нами уже решалась в п. 1.14.1. Затем перенесем в горизонтальной плоскости груз в место его фактического приема. При этом могут появиться крен и дифферент. Как следует из п.1.14.1, чтобы при приеме малого груза не возникало крена и дифферента, ЦТ груза должен располагаться на одной вертикали с ЦТ площади ватерлинии. Поэтому примем вначале груз в точку с координатами x f, 0, zp, где аппликата z p может быть любой. Изменение средней осадки определится формулой (1.93) Найдем изменение поперечной метацентрической высоты. В соответствии с первой формулой (2.29) Изменение аппликаты ЦТ судна определяется формулой (1.97) а изменение аппликаты ЦВ - формулой (1.100) Изменение поперечного метацентрического радиуса равно Подставляя значения Отсюда поперечная метацентрическая высота после приема груза равна Аналогичным путем определяется изменение продольной метацентрической высоты Изменение продольного метацентрического радиуса находим аналогично (2.42), считая судно прямобортным После подстановки значений Для большинства судов величина Тогда продольная метацентрическая высота после приема груза будет равна В случае расходования груза величину p следует вводить в формулы (2.42) и (2.46) со знаком минус. Найдем изменение коэффициентов остойчивости, входящих в выражения (2.14а) и (2.15). Умножая (2.42) и (2.47) на величину и для коэффициента продольной остойчивости Следовательно, для большинства надводных судов приближенно можно считать, что при приеме и расходовании малого груза коэффициент продольной остойчивости не изменяется. Перейдем ко второй части операции: переместим груз в горизонтальной плоскости так, чтобы его ЦТ оказался в точке с координатами xp и yp. Изменение посадки судна вследствие такого перемещения определим по формулам (2.36) и (2.37), в которых следует положить ly = yp; lx = xp — xf. Тогда с учетом (2.47) и (2.48) углы крена и дифферента будут равны а дифферент судна (в метрах) Изменения осадок носом и кормой найдем как алгебраическую сумму изменений средней осадки и осадки каждой из оконечностей, обусловленных малым равнообъемным наклонением на угол Отсюда изменение осадки на мидель-шпангоуте равно где После приема груза средняя осадка равна а осадка на миделе где Проанализируем, как изменяются начальные метацентрические высоты при приеме (расходовании) малого груза в разные места по высоте судна. Рассматривая формулу (2.41), видим, что при аппликате ЦТ груза, равной изменение поперечной метацентрической высоты Рассматривая приближенную формулу (2.45), определяющую изменение продольной метацентрической высоты, видим, что для большинства надводных судов прием любого малого груза приводит к уменьшению продольной метацентрической высоты, а любое расходование — к ее увеличению. Это объясняется расположением соответствующей нейтральной плоскости, которая согласно (2.44) приближенно описывается уравнением и, следовательно, практически всегда лежит ниже основной плоскости. Значит, груз, принятый или израсходованный в любом месте на судне, оказывается выше нейтральной плоскости, что должно приводить к уменьшению метацентрической высоты в случае приема и к ее увеличению в случае расходования груза. Посмотрим, как изменяется при приеме или расходовании груза в разных местах по высоте коэффициент поперечной остойчивости. Приравнивая нулю второй член правой части (2.47), определяющий это изменение, получим аппликату ЦТ груза прием или расходование которого не вызовет изменения коэффициента остойчивости. Прием груза выше плоскости Прием и расходование относительно большого груза. Расчет изменения посадки и остойчивости при приеме или расходовании большого груза (превышающего 5 - 10% от водоизмещения) в первом приближении проводится с помощью метацентрической диаграммы и метацентрических формул остой-чивости. Как и в случае приема малого груза, операцию приема большого груза условно разбиваем на две части. Вначале считаем, что груз принят таким образом, что не возникает ни крена, ни дифферента. Это будет иметь место, если ЦТ принятого груза располагается на одной вертикали с ЦВ дополнительно вошедшего в воду объема толщиной Изменение средней осадки
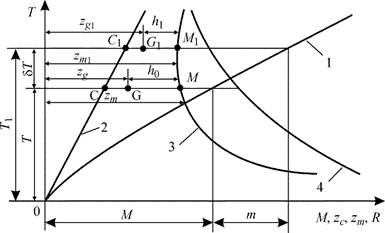
Рис. 2.16. Метацентрическая диаграмма
Чтобы найти метацентрические высоты после приема груза, рассчитываем измененную аппликату zg 1 ЦТ судна. Используя теорему о статических моментах, имеем
откуда Откладывая на горизонтальной прямой, отвечающей осадке T 1, в масштабе zm вычисленное значение zg 1, поперечную метацентрическую высоту получаем как разность: Переходим ко второй части операции — переносу груза в горизонтальной плоскости в заданную точку с координатами xp и yp. Поперечное перемещение груза будет равно ly = yp, а продольное - lz = xp — xcp,. В первом приближении углы крена и дифферента можно определить по формулам (2.36), которые в данном случае примут вид Эти формулы можно несколько уточнить, если возникающие при переносе большого груза углы крена и дифферента считать конечными и плечи кренящего и дифферентующего моментов определять с учетом их изменения пропорционально
откуда для углов крена и дифферента получаем Формулы (2.62) дают значения только двух параметров: углов вычисленная в предположении, что наклонение судна на угол
|
||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 283; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.73.221 (0.014 с.) |

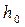 из формулы (2.18):
из формулы (2.18):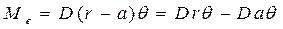 .
.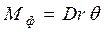 , (2.26)
, (2.26)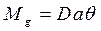 , (2.27)
, (2.27)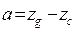 , т.е. момент
, т.е. момент 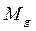 зависит от положения центра тяжести.
зависит от положения центра тяжести.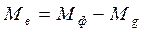 .
. 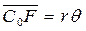 , т.е.
, т.е. 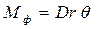 , направленный против наклонения, и второй
, направленный против наклонения, и второй 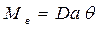 , направленный в сторону наклонения, с плечом
, направленный в сторону наклонения, с плечом 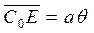 , т.е.
, т.е.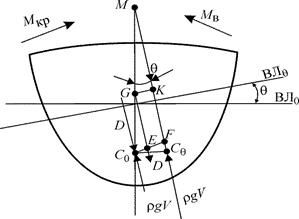
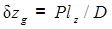 . (2.28)
. (2.28)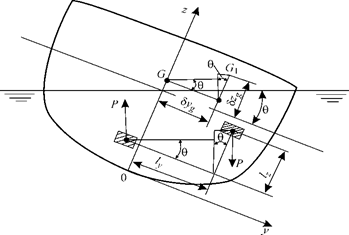
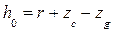 ;
;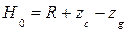 .
.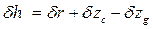 ;
;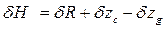 . (2.29)
. (2.29)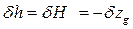 . (2.30)
. (2.30)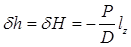 , (2.31)
, (2.31)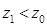 ,
, 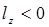 и согласно формуле (2.31)
и согласно формуле (2.31) 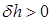 , т. е. начальная остойчивость увеличивается.
, т. е. начальная остойчивость увеличивается.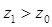 ,
, 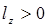 и
и 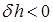 , т. е. начальная остойчивость снижается. Очевидно, возможен случай, когда при переносе грузов вверх поперечная метацентрическая высота станет равной нулю или даже отрицательной. На практике таких случаев следует избегать, поскольку они запрещены правилами безопасной эксплуатации судов.
, т. е. начальная остойчивость снижается. Очевидно, возможен случай, когда при переносе грузов вверх поперечная метацентрическая высота станет равной нулю или даже отрицательной. На практике таких случаев следует избегать, поскольку они запрещены правилами безопасной эксплуатации судов.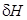 почти всегда можно пренебречь по сравнению с
почти всегда можно пренебречь по сравнению с 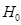 .
.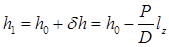 ;
;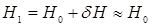 . (2.32)
. (2.32)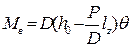 ; (2.33)
; (2.33)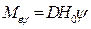 . (2.34)
. (2.34)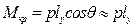 . Статическое равновесие наступает при равенстве кренящего и восстанавливающего моментов
. Статическое равновесие наступает при равенстве кренящего и восстанавливающего моментов 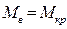 , или с учетом (2.33)
, или с учетом (2.33)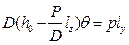 . (2.35)
. (2.35)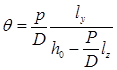 . (2.36)
. (2.36) 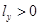 и
и 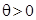 , а в случае переноса на левый
, а в случае переноса на левый 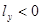 и
и 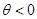 .
.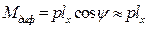 и все рассуждения относительно равенства дифферентующего и восстанавливающего моментов можно повторить. Окончательно получим угол дифферента
и все рассуждения относительно равенства дифферентующего и восстанавливающего моментов можно повторить. Окончательно получим угол дифферента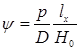 . (2.37)
. (2.37) 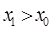 ,
, 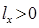 , а значит и
, а значит и 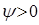 , т. е. судно получает дифферент на нос. Если же груз переносится в корму, то
, т. е. судно получает дифферент на нос. Если же груз переносится в корму, то 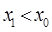 ,
, 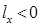 ,
, 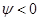 , т. е. судно дифферентуется на корму. Изменение осадок носом и кормой можно определить, используя теорему Эйлера. Проведем через точку F — ЦТ площади ватерлинии В0Л0 судна в прямом положении — наклонную ватерлинию В
, т. е. судно дифферентуется на корму. Изменение осадок носом и кормой можно определить, используя теорему Эйлера. Проведем через точку F — ЦТ площади ватерлинии В0Л0 судна в прямом положении — наклонную ватерлинию В 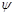 Л
Л 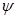 (рис. 2.15). Тогда для изменения осадок носом
(рис. 2.15). Тогда для изменения осадок носом 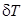 и кормой
и кормой 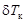 можно записать:
можно записать: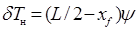 ;
; 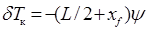 , (2.38)
, (2.38)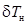 и
и 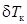 соответствуют увеличению осадок носом T н и кормой T к, а отрицательные – их уменьшению. Дифферент (в метрах) определяется выражением:
соответствуют увеличению осадок носом T н и кормой T к, а отрицательные – их уменьшению. Дифферент (в метрах) определяется выражением: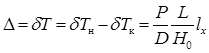 . (2.39)
. (2.39)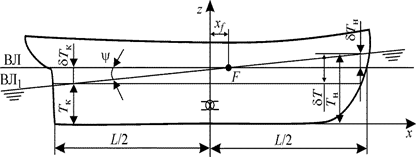
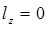 , т.е. груз переносится только по горизонтали
, т.е. груз переносится только по горизонтали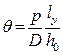 ; (2.36’)
; (2.36’)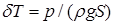 .
.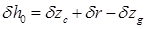 .
. 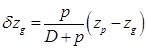 ,
,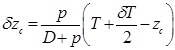 .
.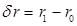 , где
, где 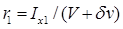 — метацентрический радиус после приема груза;
— метацентрический радиус после приема груза; 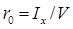 — метацентрический радиус до его приема. В формулах для r 1 и r 0 величина
— метацентрический радиус до его приема. В формулах для r 1 и r 0 величина 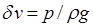 , а I x 1, и I x — моменты инерции площади ватерлинии после и до приема груза соответственно. Поскольку принятый груз полагаем малым и борта судна в пределах изменения осадки считаются вертикальными, площадь действующей ватерлинии неизменна и, следовательно,
, а I x 1, и I x — моменты инерции площади ватерлинии после и до приема груза соответственно. Поскольку принятый груз полагаем малым и борта судна в пределах изменения осадки считаются вертикальными, площадь действующей ватерлинии неизменна и, следовательно, 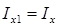 . Тогда после несложных преобразований получится
. Тогда после несложных преобразований получится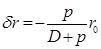 . (2.40)
. (2.40)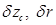 и
и 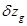 из формул (1.97), (1.100) и (2.40) в (2.39) с учетом выражения для
из формул (1.97), (1.100) и (2.40) в (2.39) с учетом выражения для 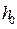 найдем
найдем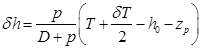 . (2.41)
. (2.41)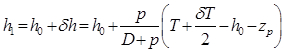 . (2.42)
. (2.42)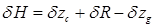 .
. 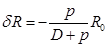 . (2.43)
. (2.43)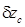 ,
, 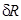 и
и 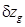 согласно формулам (1.97), (1.100) и (2.43) в
согласно формулам (1.97), (1.100) и (2.43) в 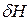 и несложных преобразований получим
и несложных преобразований получим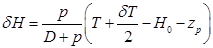 . (2.44)
. (2.44)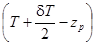 намного меньше H 0. Поэтому приближенно можно положить
намного меньше H 0. Поэтому приближенно можно положить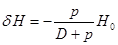 . (2.45)
. (2.45)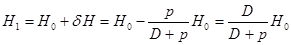 . (2.46)
. (2.46)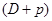 , получим для коэффициента поперечной остойчивости
, получим для коэффициента поперечной остойчивости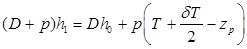 . (2.47)
. (2.47)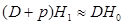 . (2.48)
. (2.48)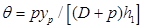 ; (2.49)
; (2.49)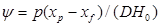 , (2.50)
, (2.50)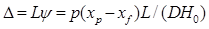 . (2.51)
. (2.51)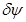 . Учитывая, что такое наклонение судна согласно теореме Эйлера происходит относительно поперечной оси, проходящей через ЦТ площади ватерлинии прямого положения для средней осадки, изменившейся на
. Учитывая, что такое наклонение судна согласно теореме Эйлера происходит относительно поперечной оси, проходящей через ЦТ площади ватерлинии прямого положения для средней осадки, изменившейся на 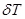 , аналогично (2.37) получим
, аналогично (2.37) получим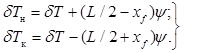 (2.52)
(2.52)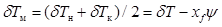 , (2.53)
, (2.53)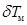 — изменение средней осадки, отсчитываемое в плоскости, проходящей через ЦТ площади начальной ватерлинии.
— изменение средней осадки, отсчитываемое в плоскости, проходящей через ЦТ площади начальной ватерлинии.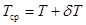 , (2.54)
, (2.54)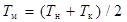 , (2.55)
, (2.55)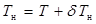 ;
; 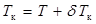 . (2.56)
. (2.56)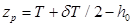 . (2.57)
. (2.57)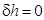 как в случае приема груза
как в случае приема груза 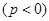 , так и в случае его расходования
, так и в случае его расходования 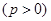 . Выражение (2.58) представляет собой уравнение горизонтальной плоскости, расположенной на высоте
. Выражение (2.58) представляет собой уравнение горизонтальной плоскости, расположенной на высоте 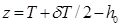 над основной. При приеме (расходовании) груза, ЦТ которого окажется на этой горизонтальной плоскости, поперечная метацентрическая высота не изменится. Такая горизонтальная плоскость называется нейтральной (иногда ее называют предельной). Если груз принят ниже нейтральной плоскости, т. е.
над основной. При приеме (расходовании) груза, ЦТ которого окажется на этой горизонтальной плоскости, поперечная метацентрическая высота не изменится. Такая горизонтальная плоскость называется нейтральной (иногда ее называют предельной). Если груз принят ниже нейтральной плоскости, т. е. 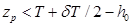 , то согласно формуле (2.41)
, то согласно формуле (2.41) 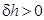 — поперечная метацентрическая высота увеличится. Если же груз принят выше нейтральной плоскости, т. е.
— поперечная метацентрическая высота увеличится. Если же груз принят выше нейтральной плоскости, т. е. 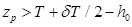 , то
, то 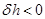 — поперечная метацентрическая высота уменьшится. В случае расходования груза получается наоборот — снятие его с плоскости, лежащей ниже нейтральной плоскости, приводит к уменьшению поперечной метацентрической высоты, снятие же груза, расположенного выше нейтральной плоскости — к ее увеличению.
— поперечная метацентрическая высота уменьшится. В случае расходования груза получается наоборот — снятие его с плоскости, лежащей ниже нейтральной плоскости, приводит к уменьшению поперечной метацентрической высоты, снятие же груза, расположенного выше нейтральной плоскости — к ее увеличению.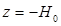 , (2.58)
, (2.58)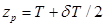 , (2.59)
, (2.59)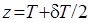 приведет к уменьшению коэффициента остойчивости, прием ниже — к его увеличению. Сопоставив (2.59) и (2.57), видим, что нейтральная плоскость для коэффициента остойчивости располагается выше на величину h 0, чем нейтральная плоскость для поперечной метацентрической высоты. Следовательно, говоря о нейтральной плоскости, необходимо указывать, об изменении какой из характеристик остойчивости при приеме груза идет речь: метацентрической высоты или коэффициента поперечной остойчивости, определяющего восстанавливающую способность судна при крене. Поскольку коэффициент продольной остойчивости для большинства надводных судов в результате приема или расходования малого груза согласно (2.54) фактически не изменяется, вопрос о различии нейтральных плоскостей для этого коэффициента и продольной метацентрической высоты практического значения не имеет.
приведет к уменьшению коэффициента остойчивости, прием ниже — к его увеличению. Сопоставив (2.59) и (2.57), видим, что нейтральная плоскость для коэффициента остойчивости располагается выше на величину h 0, чем нейтральная плоскость для поперечной метацентрической высоты. Следовательно, говоря о нейтральной плоскости, необходимо указывать, об изменении какой из характеристик остойчивости при приеме груза идет речь: метацентрической высоты или коэффициента поперечной остойчивости, определяющего восстанавливающую способность судна при крене. Поскольку коэффициент продольной остойчивости для большинства надводных судов в результате приема или расходования малого груза согласно (2.54) фактически не изменяется, вопрос о различии нейтральных плоскостей для этого коэффициента и продольной метацентрической высоты практического значения не имеет.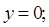
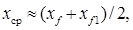 где
где 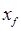 и
и 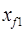 — абсциссы ЦТ площадей ватерлиний прямого положения судна до приема груза (осадка T) и после его приема (осадка
— абсциссы ЦТ площадей ватерлиний прямого положения судна до приема груза (осадка T) и после его приема (осадка 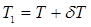 ). Они легко определяются по кривым элементов теоретического чертежа.
). Они легко определяются по кривым элементов теоретического чертежа.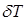 и характеристик начальной остойчивости находим с помощью метацентрической диаграммы, которая представляет собой совокупность следующих кривых (рис. 2.16): 1 — грузового размера M (T); 2 — аппликат ЦВ zc (Т); 3 — возвышения поперечного метацентра над основной линией
и характеристик начальной остойчивости находим с помощью метацентрической диаграммы, которая представляет собой совокупность следующих кривых (рис. 2.16): 1 — грузового размера M (T); 2 — аппликат ЦВ zc (Т); 3 — возвышения поперечного метацентра над основной линией 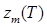 ; 4 — продольного метацентрического радиуса
; 4 — продольного метацентрического радиуса 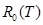 . Откладывая по оси абсцисс водоизмещение М, находим по грузовому размеру исходную осадку Т; откладывая M + m, находим изменение осадки
. Откладывая по оси абсцисс водоизмещение М, находим по грузовому размеру исходную осадку Т; откладывая M + m, находим изменение осадки 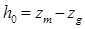 . Снимая с диаграммы значения zc и R 0 для осадки T, исходную продольную метацентрическую высоту вычисляем по формуле
. Снимая с диаграммы значения zc и R 0 для осадки T, исходную продольную метацентрическую высоту вычисляем по формуле 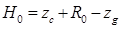 .
. 
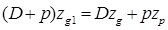 ,
,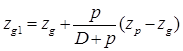 . (2.60)
. (2.60)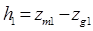 . Сняв с диаграммы для осадки T 1 значения z с 1 и R 1 продольную метацентрическую высоту после приема груза рассчитываем по формуле
. Сняв с диаграммы для осадки T 1 значения z с 1 и R 1 продольную метацентрическую высоту после приема груза рассчитываем по формуле 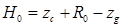 .
.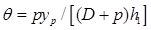 ;
;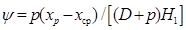 . (2.61)
. (2.61)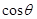 и
и 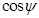 ‚ а восстанавливающие моменты рассчитывать по метацентрическим формулам остойчивости, в которые вместо углов
‚ а восстанавливающие моменты рассчитывать по метацентрическим формулам остойчивости, в которые вместо углов 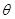 и
и 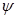 входят их синусы. Тогда условия равновесия примут вид
входят их синусы. Тогда условия равновесия примут вид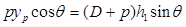 ;
;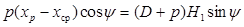 ,
,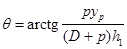 ;
; 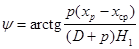 . (2.62)
. (2.62)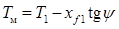 , (2.63)
, (2.63)


