
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Некоторые задачи плавучести, решаемые в процессе эксплуатации суднаСодержание книги
Поиск на нашем сайте
В процессе эксплуатации на судне расходуются грузы (вода, топливо и т. д.) или, наоборот, принимаются грузы. Кроме того, судно эксплуатируется в морях с водой различной плотности, зависящей от солености и температуры. При этом будет наблюдаться изменение осадки и координат ЦТи ЦВ. Контроль за ними является обязательным, поскольку от знания их зависит безопасность судна.
1.14.1. Изменение осадки и координат ЦТ и ЦВпри приеме и расходовании малого груза. Кривая числа тонн на 1 см осадки Груз называется малым, если при его приеме или расходовании судно в пределах изменения осадки можно считать прямобортным. На практике считается, что условие прямобортности для судов обычных архитектурных типов выполняется, если масса груза не превосходит 10 % массы судна. При приеме малого груза весом p = mg (рис. 1.35) осадка судна Поскольку груз мал, можно в пределах изменения осадки считать борта судна вертикальными и выразить δ V через приращение осадки и площадь ватерлинии δ V = S δ T, (1.91) тогда p = ρ gS δ T. (1.92) δ T = p /(ρ gS). (1.93) С помощью формулы (1.93) и с учетом того, что p = mg, можно рассчитать и построить кривую числа тонн на 1 см осадки. Если положить δ T = 1 см = = 0,01 м, а m = q, получим q = ρ S /100 - (1.94) δ T = m / q. (1.95) В проектной документации обычно рядом с грузовой шкалой изобра- При приеме груза кроме осадки будут меняться также координаты Обозначив координаты центра тяжести груза где
Рис.1.35. К определению изменения осадки и приращений координат ЦТ и ЦВ при приеме малого груза: а — поперечный; б — продольный разрез судна Из системы уравнений (1.96) легко определить изменения координат ЦТ судна: В соответствии с (1.97) получается, что изменения координат ЦТне будет, если груз принят в ЦТ судна. Изменение координатЦВ можно определить из уравнений статических моментов объемов относительно координатных плоскостей: Здесь Из рис. 1.35 следует, что при приеме малого груза Подставив эти величины в уравнения (1.98), можем вычислить Умножив числители и знаменатели уравнений (1.99) на ρ g, получим Системы (1.97) и (1.100) верны и для случая снятия груза, но только Формулы (1.97) и (1.100) используют в дальнейшем при расчетах остойчивости. Чтобы судно не получило при приеме или снятии груза ни крена, ни дифферента, необходимо выполнять условия δ xg = δхс и δ yg = δус ,или в развернутом виде на основании выражений (1.97) и (1.100) С учетом того, что х g = хс (из второго условия плавучести), окончательно имеем хр = х f,; у f = 0. (1.102) Таким образом, чтобы судно при приеме или расходовании груза не получило ни крена, ни дифферента, центр тяжести этого груза должен находиться на одной вертикали с центром тяжести площади ватерлинии. Определение углов крена и дифферента в случае приема груза в произвольную точку связано с достаточно сложными расчетами и выполняется в дальнейшем.
|
||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 175; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.134.196 (0.006 с.) |

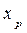 ,
, 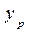 и
и 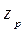 (рис.1.35) и составив уравнения статических моментов масс относительно координатных
(рис.1.35) и составив уравнения статических моментов масс относительно координатных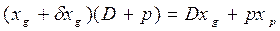 ;
; 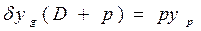 ; (1.96)
; (1.96) 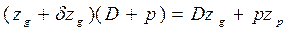 ,
,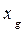 ,
, 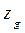 — координаты ЦТ судна до приема груза. При написании второго уравнения учтено, что для судна в прямом положении
— координаты ЦТ судна до приема груза. При написании второго уравнения учтено, что для судна в прямом положении 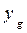 =0.
=0.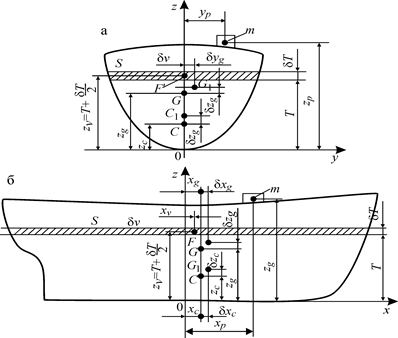
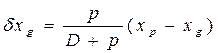 ;
;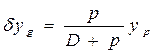 ; (1.97)
; (1.97)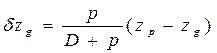 .
.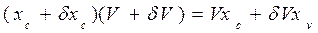 ;
;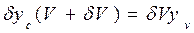 ; (1.98)
; (1.98)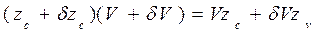 .
.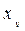 ,
, 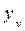 и
и 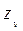 — координаты ЦТдополнительного объема δ V.
— координаты ЦТдополнительного объема δ V.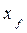 ;
; 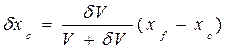 ;
;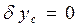 ; (1.99)
; (1.99)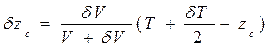 .
.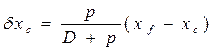 ;
;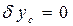 ; (1.100)
; (1.100)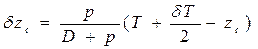
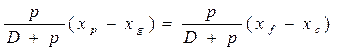 ;
;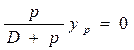 (1.101) (1.101
(1.101) (1.101


