Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Площадь шпангоута. Интегральные кривые Власова. Масштаб БонжанаСодержание книги
Поиск на нашем сайте
Формулу для определения площади погруженной части шпангоута можно получить, воспользовавшись приемом, описанным ранее при определении, например, площади ватерлинии. Выделим элемент площади шпангоута d Ω = 2 ydz (рис. 1.25). Вся площадь будет равна Если необходимо получить зависимость Ω (z), то формулу (1.79) пред-
Рис. 1.25. К определению элементов площади шпангоута
Часто требуется знать не полную площадь шпангоута Ω, а половину этой площади а также статические моменты b и с половины площади относительно
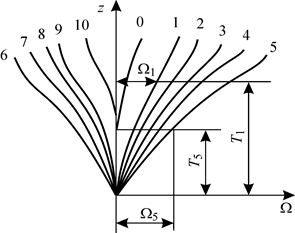
Рис. 1.26. Интегральные кривые Власова. К определению погруженной площади шпангоута для судна, сидящего с креном и дифферентом
Совокупность кривых площадей всех шпангоутов Ω называется
Рис. 1.27. Масштаб Бонжана
Иногда вместо кривых Ω (z) на следах шпангоутов наносят шкалы Ω (рис. 1.28). Строить такой масштаб Бонжана несколько труднее, хотя в решении практических задач пользоваться им удобнее.
Рис. 1.28. Второй вариант масштаба Бонжана Еще один вариант масштаба Бонжана - совмещенный - изображен на рис.1.29. Все кривые площадей шпангоутов строят при одной вертикальной оси: справа для носовых шпангоутов и мидель-шпангоута, слева для кормовых. Такой масштаб Бонжана занимает меньше места, однако пользоваться им значительно труднее, чем предыдущими.
Рис. 1.29. Третий вариант масштаба Бонжана
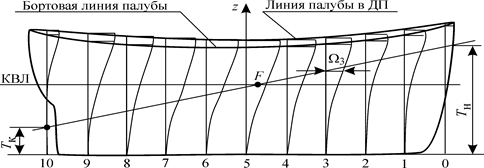
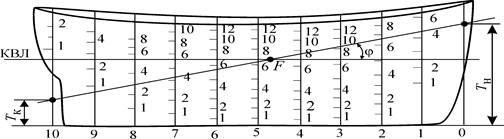
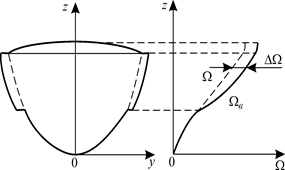
Применяют масштаб Бонжана при определении водоизмещения V и абсциссы хс для судна, плавающего с дифферентом. Вычисление водоизмещения с учетом выступающих частей и соответствующей абсциссы хс удобно производить по масштабу Бонжана, в котором к площадям шпангоутов введены поправки на выступающие части, попадающие в шпангоутное сечение. Пример учета выступающих частей приведен на рис. 1.30. На каждой ватерлинии вправо от кривой Ω (z) откладывают дополнительную площадь шпангоута ΔΩ. С учетом выступающих частей площадь шпангоута будет равна
Рис. 1.30. Масштаб Бонжана с учетом выступающих частей
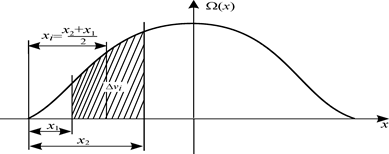
В последнее время в расчетах статики, входящих в САПР, исполь- Объем теоретического отсека вычисляют как разность V 2 i - V 1 i. Абсциссу центра тяжести объема этого отсека определяют по формуле х i = (х 2 i + х 1 i)/2. На отрезке горизонтальной прямой, равной длине судна в масштабе, наносят точки, соответствующие выбранным абсциссам х i, из которых восстанавливают перпендикуляры. Затем на каждой выбранной ватерлинии в масштабе откладывают объемы отсеков Δ v i = V 2 i - V 1 i. Полученное семейство кривых аналогично масштабу Бонжана. Для произвольной ватерлинии путем суммирования всех объемов отсеков легко получить объемное водоизмещение для заданных значений осадок кормой Тк и носом Тн. Подобные кривые могут быть построены и для статических моментов выбранных отсеков относительно координатных плоскостей, что позволяет определить координаты ЦВ.
Рис. 1.31. Определение объема отсека между двумя абсциссами
1.12. Определение водоизмещения и координат ЦВдля различных случаев посадки судна. Диаграмма Фирсова Для судна, сидящего прямо и на ровный киль, определение водо-
|
||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 1075; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.009 с.) |

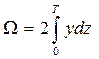 . (1.79)
. (1.79)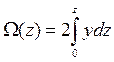 . (1.80)
. (1.80)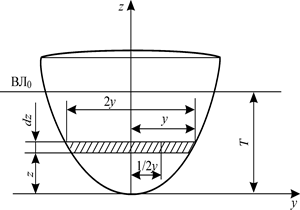
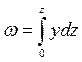 , (1.81)
, (1.81)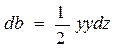 ;
; 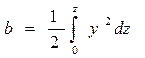 ; (1.82)
; (1.82)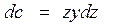 ;
; 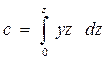 . (1.83)
. (1.83) 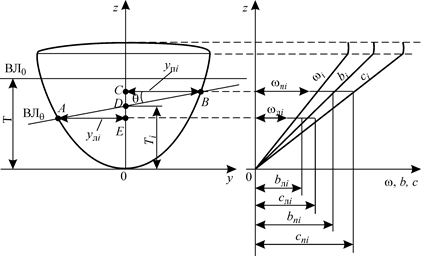
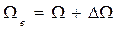 .
.
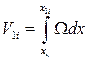 ;
; 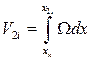 .
.