
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Напряженность и потенциал электрического поля.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Электрическое поле — это особый вид материи, существующий вокруг заряженных тел или заряда. Силовой характеристикой электрического поля является напряженность. Обозначается напряженность
Е – напряженность электрического поля, F – сила действующая на заряд, q – электрический заряд. Направление вектора напряженности в любой точке электрического поля совпадает с направлением силы, действующей заряд. Напряженность является параметром каждой точки электрическою поля и не зависит от величины от заряда q. Напряженность электрического поля, созданного несколькими зарядами в какой-либо точке этого поля, определяется геометрической суммой напряженностей, созданных в этой точке каждым точечным зарядом: Для наглядности электрическое поле изображают силовыми линиями. Силовые линии направлены от положительного заряда к отрицательному. Линия проводится так, чтобы вектор напряженности поля в данной точке являлся касательной к ней (рис.). Электрическое поле называют однородным, если напряженность его во всех точках одинакова по величине и направлению. Однородное электрическое поле изображается параллельными линиями, расположенными на одинаковом расстоянии друг от друга. Для энергетической характеристики каждой точки электрического поля вводится понятие «потенциал». Обозначается потенциал буквой Электрический потенциал – работа, которую нужно выполнить, чтобы перенести единицу заряда (1Кл) из данной точки в бесконечность или
Потенциал — скалярная величина. Если электрическое поле создано несколькими зарядами, то потенциал в каждой точке поля определяется алгебраической суммой потенциалов, созданных в этой точке каждым зарядом. Заряд перемещается из точки с большим потенциалом в точку с меньшим потенциалом. Между двумя точками с равными потенциалами заряд перемещаться не будет. Для перемещения заряда между двумя точками электрического поля должна быть разность потенциалов в этих точках. Разность потенциалов между двумя точками характеризует напряжение
Кроме того, напряжение между двумя точками электрического поля характеризуется энергией, затраченной на перемещение единицы положительного заряда между этими точками, т. е.
Между напряжением и напряженностью в однородном электрическом поле (рис.) существует зависимость
Отсюда видно, что напряжение - это работа, затрачиваемая на перенос единицы заряда (1Кл) из точки 1 в точку 2 поля напряженностью В общем случае для неоднородного электрического поля значение напряжения определяется Постоянный электрический ток.
Явление направленного движения свободных носителей электрического заряда в веществе или вакууме называется электрическим током. Условиями возникновения электрического тока являются: 1) наличие источника электрической энергии; 2) замкнутость пути, по которому перемещаются заряды. Обозначается величина постоянного тока буквой I. Измеряется ток в амперах, т.е. А (ампер). Величина тока I определяется количеством электричества (зарядов) q, проходящим через поперечное сечение проводника в единицу времени t:
Постоянным называется ток, величина и направление которого не изменяется с течением времени. За направление постоянного тока в замкнутой электрической цепи принимается направление от положительного полюса источника к его отрицательному полюсу по внешнему участку цепи, т. е. от «+» к «-». Силу электрического тока измеряют с помощью амперметра. Амперметр включается в цепь последовательно. Причем в цепях постоянного тока клемма со знаком «+» подключается в направлении положительного полюса источника энергии, а клемма со знаком «–» в сторону отрицательного полюса источника энергии. На практике вместо силы тока, часто используют плотность. Обозначается плотность тока буквой J. Отношение величины тока в проводнике I к площади его поперечного сечения S характеризует плотность тока в этом проводнике.
Единицей измерения плотности тока является А/м
Электродвижущая сила (ЭДС).
Электрическую энергию можно получить из других видов энергии при наличии сторонней силы. Сторонние силы – это любые силы неэлектростатистического происхождения. Величина, характеризующая способность сторонних сил вызывать электрический ток, называется электродвижущей силой (ЭДС). Единицей измерения ЭДС является вольт. ЭДС характеризуется энергией, которую затрачивает или может затратить источник на перемещение единицы положительного заряда по всей замкнутой цепи:
Источники энергии постоянного тока. Источники ЭДС и тока
К источникам энергии постоянного тока относят гальванические элементы аккумуляторы и т. п. Принципом действия гальванических элементов и аккумуляторов является электролиз.
Источник электродвижущей силы – это источники электрической энергии, характеризирующейся электродвижущей силой E и внутренним электрическим сопротивлением Rвн. За положительное направление ЭДС источника принимается направление возрастания потенциала внутри этого источника.
Внутреннее сопротивление Rвн показывает, что часть энергии, вырабатываемой источником, используется внутри источника. Поэтому, напряжение на выходах источника равна разности между ЭДС источника и падением напряжения на внутреннем сопротивлении и определяется по формуле:
При напряжении U = 0 ток источника равен току короткого замыкания:
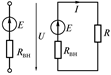
Источник электрической энергии с малым внутренним сопротивлением можно заменить идеализированной моделью, для которой Rвн= 0. Такой идеализированный источник электрической энергии называется идеальным источником ЭДС с одним параметром Е = U. Напряжение между выводами идеального источника ЭДС не зависит от тока, а его внешняя характеристика определяется выражением: U = Е = const. Источник электрической энергии с большим внутренним сопротивлением называется источником тока. При Rвн >> Rн:
Отсюда видно, что ток источника тока не зависит от напряжения между его выводами.
Закон Ома для участка цепи.
Закон Ома для участка электрической цепи устанавливает зависимость между током, напряжением и сопротивлением на этом участке цепи. Математическое выражение закона Ома для участка имеет вид:
Часто место сопротивления пользуются проводимостью. Проводимость – это величина обратная сопротивлению Тогда закон Ома для участка цепи можно записать так Для замкнутой электрической цепи ЭДС источника, можно определить выражением
Из формулы 1.14 следует, что ток в замкнутой цепи равен
Первый закон Кирхгофа.
Первый закон Кирхгофа говорит о том, что в любой момент времени количество электрических зарядов, направленных к узлу, равно количеству зарядов, направленных от узла, откуда следует, что электрический заряд в узле не накапливается. Поэтому алгебраическая сумма токов в ветвях, сходящихся в узле электрической цепи, равна нулю:
До написания уравнения (1.18) необходимо задать условные положительные направления токов в ветвях, обозначив эти направления на схеме стрелками. В уравнении (1.18) токи, направленные к узлу, записывают с одним знаком (например, с плюсом), а токи, направленные от узла, с противоположным знаком (с минусом).
Второй закон Кирхгофа.
Второй закон Кирхгофа отражает положение о том, что изменение потенциала во всех элементах контура в сумме равно нулю. Из этого следует такая формулировка второго закона Кирхгофа: в любом контуре электрической цепи постоянного тока алгебраическая сумма ЭДС равна алгебраической сумме падений напряжений на всех элементах этого контура:
При составлении уравнений по второму закону Кирхгофа предварительно задают условные положительные направления токов во всех ветвях электрической цепи и для каждого контура выбирают направление обхода. Если при этом направление ЭДС совпадает с направлением обхода контура, то такую ЭДС берут со знаком плюс, если не совпадает — со знаком минус. Падения напряжений в правой части уравнения (1.19) берут со знаком плюс, если положительное направление тока в данном элементе цепи совпадает с направлением обхода контура, если не совпадает — со знаком минус.
Последовательное и параллельное соединение элементов электрической цепи.
Если несколько резисторов соединены один за другим без разветвлений и по ним протекает один и тот же ток, такое соединение называется последовательным. При таком соединении: I = const, Если сопротивления равны, т. е Параллельным соединением приемников называется такое соединение, при котором к одним и тем же двум узлам электрической цепи присоединяется несколько ветвей. При таком соединении: U = const, Если сопротивления равны, то
Последовательное и параллельное соединение ЭДС. При последовательном соединении ЭДС один источник ЭДС следует за другим. Возможны два случая включения последовательно: согласованное и встречное. При согласованном включении ЭДС складываются при встречном вычитаются. По второму закону Кирхгофа можем записать:
Отсюда
При последовательном соединении
При параллельном соединении источников с одинаковыми параметрами их общая ЭДС не изменится, но уменьшатся токи через каждый источник и внутреннее сопротивление общего источника. При
Метод контурных токов
Этот метод расчета основан на том, что действительный (истинный) ток в любой ветви, входящей в несколько контуров (например, на рис.1 ветвь с сопротивлением R5 входит в контур абе и в контур бвде), можно представить в виде алгебраической суммы токов, каждый из которых замыкается по своему контуру.
Исходя из этого, сложную цепь можно разбить на ряд контуров и считать, что в каждой ветви данного контура протекает одинаковый ток. Этот ток называют контурным. Направление его выбирают произвольно. Контурные токи и будут теми неизвестными, которые нужно определить. Зная значения и направления контурных токов, можно определить действительный ток в каждой ветви цепи: a) ток в ветви, входящий в данный контур, равен контурному току; b) ток в ветви, входящий в несколько контуров, равен алгебраической сумме контурных токов. Как определить контурные токи? Для каждого контура составляют уравнения по второму закону Кирхгофа, причем при составлении уравнений контур обходят по направлению контурного тока. При этом необходимо учитывать падение напряжения в смежной с другим контуром ветви от контурного тока смежного контура. Это падение напряжения будет положительным, если направление контурного тока в смежном контуре совпадает с направлением обхода данного контура и отрицательным, если направление контурного тока не совпадает с направлением обхода. Значение э.д.с. берется со знаком плюс, если направление обхода контура совпадает с направлением действия э.д.с., и со знаком минус – если не совпадает. При выборе контуров руководствуются следующим:
N=b-y+1 (1.33) где b – число ветвей; y – число узлов;
На примере расчета цепи, представленной на рис.1, поясним сказанное выше.
1-й контур – I11, 2-й контур – I22, 3-й контур – I33.
1-й контур:
2-й контур:
= (1) 3-й контур:
I1=I11, I2=I22, I3=I33, I4=I22, I5=I11-I22, I6=I22-I33. Для решения системы уравнений, составленной по второму закону Кирхгофа, целесообразно применить метод определителей. Тогда в общем виде эта система уравнений записывается следующим образом:
и т.д. Поясним смысл каждого члена уравнений. a) В левой части каждого уравнения стоят суммарные значения э.д.с., входящие в контур. Они имеют знак плюс, если направление обхода контура и направление действия суммарной э.д.с. совпадают. Для цепи на рис.1: E11=E1, E22=0, E33=-E2 b) Сопротивление R11, R22, R33 – собственные сопротивления I, II, III контуров соответственно. Собственные сопротивления контуров для цепи на рис.1: R11=R1+R5, R22=R2+R5+R4+R6, R33=R3+R6 c) Сопротивления R12, R21, R13, R31 и т.п. – общие или смежные сопротивления контуров. Смежное (общее) сопротивление представляет собой сопротивление ветви, входящей в несколько контуров. Его обозначают с индексом, состоящим из номеров контуров, в которые входит ветвь. Для цепи на рис.1 смежные сопротивления: для I контура R12, для II контура R21, для II контура R23, для III контура R32. Если через общее сопротивление контурные токи смежных контуров протекают в разных направлениях, в уравнение (2) такое общее сопротивление ставится со знаком минус. В цепи на рис.1 через все смежные сопротивления токи текут в разных направлениях и в этом случае принимают, что R12=R21=-R5; R23=R23=-R6. Для составления определителя необходимо, чтобы все уравнения имели одинаковое число членов. В правую часть каждого уравнения записываются произведения всех контурных токов на соответствующие сопротивления, а в случае, если это сопротивление не входит в рассматриваемый контур, его принимают равным нулю. Составим уравнения для 3-х контуров на рис.1, учитывая сделанные замечания.
Если в эти уравнения поставить значения каждого члена и учесть сказанное о знаках, получим уравнение (1). Покажем, как решается система уравнений (2) методом определителей. Ток К-го контура равен
где
Каждый частный определитель Например, если определяется ток I – го контура, частный определитель будет иметь вид
При расчете цепи методом контурных токов можно не составлять уравнения по 2 – ому закону Кирхгофа, а достаточно составить определители по уравнениям (5), (6) и по уравнению (5) рассчитать контурные токи. При составлении определителей нельзя забывать о знаках перед членами определителя (перед э.д.с. ставят знак минус, если направление обхода и направление действия э.д.с. не совпадают, перед общими сопротивлениями ставят знак минус, если контурные токи тех контуров, в которые входят эти сопротивления, направлены в разные стороны).
Метод наложения
Метод наложения основан на принципе независимости действия э.д.с. Согласно этому принципу токи, протекающие в цепи при наличии нескольких э.д.с., можно представить как алгебраическую сумму токов, создаваемых каждой из э.д.с. в отдельности. Вначале определяются значения токов в ветвях, создаваемых действием только одного источника (например, для рис.1 I1, I2, I3, I4, I5, I6 от Е1, полагая Е2=0). Затем таким же образом определяют токи в ветвях, создаваемые действием другого источника (например, для рис.1 токи I1//, I2//, I3//, I4//, I5//, I6// от Е2, полагая Е1=0). Затем находятся действительные токи в ветвях, как алгебраические суммы токов, создаваемые в одних и тех же ветвях отдельными источниками. Рассмотрим порядок определения токов, создаваемых отдельными э.д.с. на примере схемы рис.1. Вначале находятся токи в ветвях и их направления при действии только одной э.д.с., например, Е1, когда Е2=0. Для этого определяется общее сопротивление цепи R/общ (внутренним сопротивлением источника э.д.с. Е2 пренебрегаем).
После этого определяются токи в ветвях схемы рис.1 при действии только э.д.с. Е1, а именно:
Затем составляется схема рис.1 при действии Е2 (Е1=0, внутреннее сопротивление источника э.д.с. пренебрегаем) и наносятся направления токов I1//, I2//, I3//, I4//, I5//, I6//. Аналогично вышеизложенному рассчитываются токи, создаваемые действием источника Е2. Действительные токи в ветвях определяются как алгебраическая сумма составляющих токов, проходящих через соответствующие ветви:
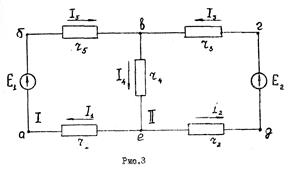
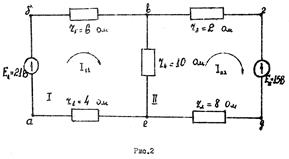
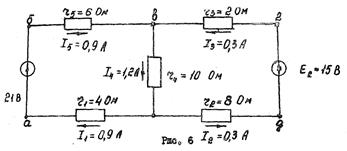
Составляется третья схема, на которой наносится направления действительных токов. Направление действительных токов в ветвях выбирается по большему составляющему току в каждой цепи. Пример расчета линейной цепи методом контурных токов. Найти токи в схеме рис.2. Численные значения сопротивлений и э.д.с. указаны на рисунке.
Решение. В этой схеме два независимых контура I и II (N=3-2+1). Выбираем произвольно направление контурных токов I11 и II22 по часовой стрелке. Система уравнений согласно второму закону Кирхгофа для данной цепи запишется в следующем виде:
Определяем собственные сопротивления контуров:
Сопротивление смежной ветви R12=R21=-r4. Внутренними сопротивлениями источников пренебрегаем. Контурные э.д.с. равны: E11=E1=21 B, E22=-E2=-15 B. Перед э.д.с. E2 знак минус, так как направление обхода контура не совпадает с положительным направлением действия э.д.с. При составлении уравнения по второму закону Кирхгофа направление обхода контуров принимаем совпадающим с направлением контурных токов. В соответствии с численными значениями, полученными для R11, R12, R21, R22, E11 и E22, с учетом знаков уравнения перепишутся следующим образом:
Главный определитель системы
Контурные токи I11 и I22 будут равны:
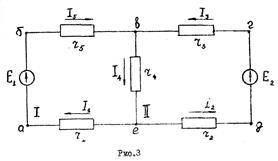
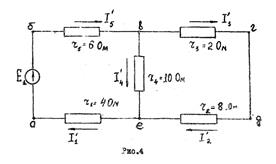
После подсчета контурных токов определяются действительные токи в ветвях: I1=I5=I11=0,9A; I2=I3=I22=-0,3A; I4=I11-I22=1,2A Значение контурного тока I22 получилось отрицательным, поэтому истинное направление его будет обратным принятому на рис.2. Истинные направления токов во всех ветвях показаны стрелками на рис.3.
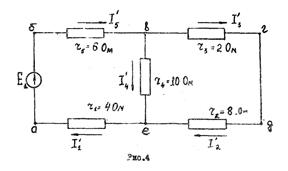
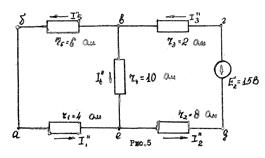
Пример расчета линейной цепи методом наложения. Найти этим методом токи в ветвях схемы рис.2. Решение. Исключаем из схемы э.д.с. E2. При действии в схеме рис.2 одной э.д.с. E1 примем, что токи будут иметь направления, как указано на рис.4.
Для схемы рис.4 находим общее сопротивление цепи (внутреннее сопротивление источников э.д.с. E1 и E2 принимаем равными нулю).
Затем находим токи в ветвях схемы рис.4 от действий только э.д.с. E1.
Полагая э.д.с. E1=0, находим направления и значения токов в ветвях схемы от действия э.д.с. E2.
Действительные токи в ветвях определяются алгебраическим сложением составляющих токов ветвей. Направления действительных токов в ветвях определяются по большей составляющей тока каждой ветви. Итак, для схемы рис.2 действительные токи в ветвях будут равны:
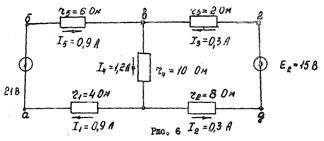
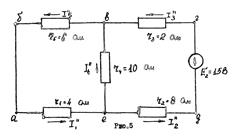
Таким образом, накладывая схему рис.4 на схему рис.5 получим схему рис.6 с действительными значениями и направлениями токов в ветвях при одновременном действии двух источников э.д.с E1 и E2.
Следует отметить, что при расчете более сложной электрической цепи, общее сопротивление эквивалентной схеме более удобно определить, разбивая всю схему, начиная со стороны противоположной действию источника э.д.с., на ряд участков, заключенных между соответствующими узлами.
Решение. В этой схеме два независимых контура I и II (N=3-2+1). Выбираем произвольно направление контурных токов I11 и II22 по часовой стрелке. Система уравнений согласно второму закону Кирхгофа для данной цепи запишется в следующем виде:
Определяем собственные сопротивления контуров:
Сопротивление смежной ветви R12=R21=-r4. Внутренними сопротивлениями источников пренебрегаем. Контурные э.д.с. равны: E11=E1=21 B, E22=-E2=-15 B. Перед э.д.с. E2 знак минус, так как направление обхода контура не совпадает с положительным направлением действия э.д.с. При составлении уравнения по второму закону Кирхгофа направление обхода контуров принимаем совпадающим с направлением контурных токов. В соответствии с численными значениями, полученными для R11, R12, R21, R22, E11 и E22, с учетом знаков уравнения перепишутся следующим образом:
Главный определитель системы
Контурные токи I11 и I22 будут равны:
После подсчета контурных токов определяются действительные токи в ветвях:
I1=I5=I11=0,9A; I2=I3=I22=-0,3A; I4=I11-I22=1,2A Значение контурного тока I22 получилось отрицательным, поэтому истинное направление его будет обратным принятому на рис.2. Истинные направления токов во всех ветвях показаны стрелками на рис.3.
Пример расчета линейной цепи методом наложения. Найти этим методом токи в ветвях схемы рис.2. Решение. Исключаем из схемы э.д.с. E2. При действии в схеме рис.2 одной э.д.с. E1 примем, что токи будут иметь направления, как указано на рис.4.
Для схемы рис.4 находим общее сопротивление цепи (внутреннее сопротивление источников э.д.с. E1 и E2 принимаем равными нулю).
Затем находим токи в ветвях схемы рис.4 от действий только э.д.с. E1.
Полагая э.д.с. E1=0, находим направления и значения токов в ветвях схемы от действия э.д.с. E2.
Действительные токи в ветвях определяются алгебраическим сложением составляющих токов ветвей. Направления действительных токов в ветвях определяются по большей составляющей тока каждой ветви. Итак, для схемы рис.2 действительные токи в ветвях будут равны:
Таким образом, накладывая схему рис.4 на схему рис.5 получим схему рис.6 с действительными значениями и направлениями токов в ветвях при одновременном действии двух источников э.д.с E1 и E2.
Следует отметить, что при расчете более сложной электрической цепи, общее сопротивление эквивалентной схеме более удобно определить, разбивая всю схему, начиная со стороны противоположной действию источника э.д.с., на ряд участков, заключенных между соответствующими узлами.
Активные и пассивные двухполюсники.
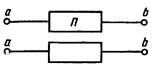
Двухполюсником называется часть сложной электрической цепи, которая имеет два зажима (входной и выходной), называемых полюсами. Двухполюсники бывают пассивные и активные. Двухполюсник, не содержащий источника энергии, называется пассивным. Линейным пассивный двухполюсник будет и тогда, когда в нем будут содержаться источники энергии, э. д. с. которых взаимно компенсируются, т. е. направлены навстречу друг другу и равны по значению. Двухполюсники условно изображают в виде прямоугольника, при этом для обозначения пассивного двухполюсника в прямоугольнике либо ставят букву П, либо не ставят никакой буквы (рис.).
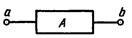
В схеме некомпенсированные двухполюсники, в которых содержатся источники электрической энергии, называются активными (рис.). В этом случае при обозначении двухполюсника в прямоугольнике ставят букву А.
При анализе электрической цепи, в которую входит пассивный двухполюсник, достаточно знать его характеристику. Так как пассивный двухполюсник является потребителем энергии, то в качестве характеристики можно взять его сопротивление, которое в этом случае называется внутренним или входным. Следовательно, на схеме замещения пассивный двухполюсник можно представить в виде одного элемента с сопротивлением, равным входному сопротивлению двухполюсника. Для активного двухполюсника наряду с сопротивлением важной характеристикой является внешняя, или вольт-амперная, характеристика, которая полностью определяет его свойства.
Электрическая энергия и работа. Мощность электрической цепи.
Работа источника электрического тока определяется по формуле:
Так как Работа и энергия – понятия равноценные. Энергия – способность источника совершать работу. Чтобы измерить энергию источника, надо измерить работу, которую он совершает, расходуя эту энергию. Измеряется энергия и работа в Джоулях (Дж). На практике за единицу энергии принимают 1 кВт·ч = 3600000 Дж. Электрическая мощность – это физическая величина, характеризующая быстроту передачи или преобразования электрической энергии:
Измеряется мощность в ваттах (Вт). Мощность, отдаваемая (полезная) источником энергии потребителю (приемнику)
Потери мощности во внутреннем сопротивлении
Условие передачи в нагрузку максимальной мощности.
Отношение мощности приемника (полезной мощности) к мощности источника энергии
Источник ЭДС развивает максимальную полезную мощность, когда внешнее сопротивление равно внутреннему сопротивлению источника:
Такой режим является невыгодным, так как 50 % энергии теряется во внутреннем сопротивлении источника
Режим цепи, при котором внешнее сопротивление цепи равно внутреннему сопротивлению источника энергии, называется режимом согласованной нагрузки. При согласованном режиме
Закон Джоуля-Ленца.
При протекании электрического тока по проводникам происходит преобразование электрической энергии в тепловую. Эта зависимость выражается формулой получившей название закон Джоуля-Ленца:
Q — количество тепла, выделенного в проводнике. Количество тепла Q измеряется иногда внесистемной единицей — калорией. 1 кал = 4,187 Дж. Отсюда, 1 Дж = 0,24кал.
Тема №3.
|
||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 13394; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.19.231 (0.015 с.) |

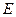 , измеряется в В/м. Напряженность каждой точки электрического поля характеризуется силой, с которой поле действует на единицу заряда, помещенного в эту точку и определяется по формуле:
, измеряется в В/м. Напряженность каждой точки электрического поля характеризуется силой, с которой поле действует на единицу заряда, помещенного в эту точку и определяется по формуле: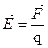 (1.1)
(1.1)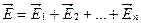 .
. , измеряется в вольтах (В).
, измеряется в вольтах (В).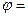
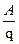 (1.2).
(1.2).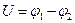 (1.3).
(1.3). (1.4).
(1.4).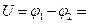
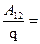
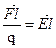 (1.5).
(1.5). по произвольному пути.
по произвольному пути.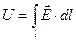 (1.6).
(1.6).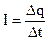 (1.7).
(1.7).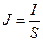 (1.8).
(1.8).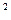 . Так как площадь сечения проводов выражают в мм
. Так как площадь сечения проводов выражают в мм 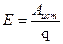 (1.9)
(1.9)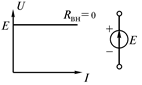
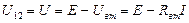 (1.10)
(1.10)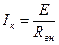 (1.11)
(1.11)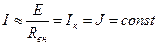 (1.12)
(1.12)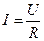 (1.13)
(1.13)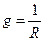 (1.14). Единицей проводимости является сименс (См).
(1.14). Единицей проводимости является сименс (См). (1.15)
(1.15)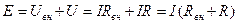 (1.16)
(1.16)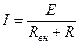 (1.17).
(1.17).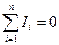 (1.18), где n — число ветвей, сходящихся в узле.
(1.18), где n — число ветвей, сходящихся в узле.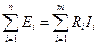 (1.19). Где n – число ЭДС в контуре; m – число элементов с сопротивлением
(1.19). Где n – число ЭДС в контуре; m – число элементов с сопротивлением 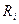 в контуре.
в контуре.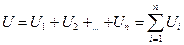 (1.20),
(1.20), 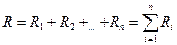 (1.21)
(1.21) , то
, то 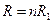 (1.22),а
(1.22),а  (1.23).
(1.23).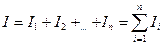 (1.24),
(1.24), 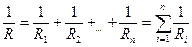 (1.25).
(1.25).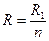 (1.26), а
(1.26), а 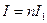 (1.27).
(1.27).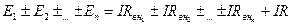 (1.28)
(1.28)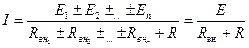 (1.29)
(1.29)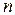 источников с одинаковыми параметрами
источников с одинаковыми параметрами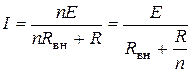 (1.30)
(1.30)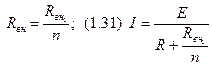 (1.32)
(1.32)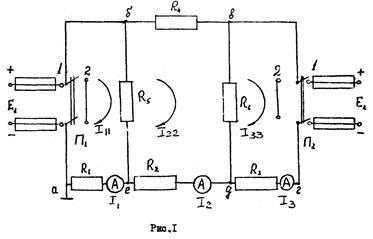
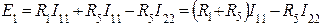
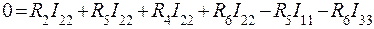 =
=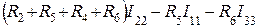
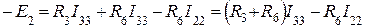
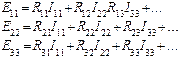 (2)
(2)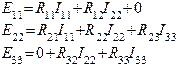 (3)
(3)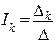 (4)
(4)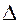 - главный определитель (детерминант);
- главный определитель (детерминант);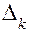 - частный определитель К – го столбца
- частный определитель К – го столбца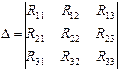 (5)
(5)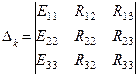 (6)
(6)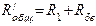 ;
; 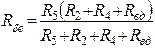 ;
; 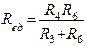
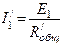 ;
; ;
;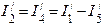 ;
;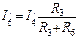 ;
;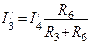 .
.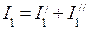 ;
; 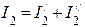 и т.д.
и т.д.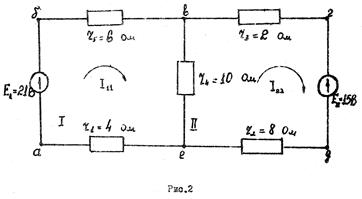

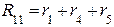 =4+10+6=20 Ом
=4+10+6=20 Ом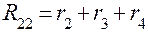 =8+2+10=20 Ом
=8+2+10=20 Ом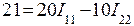
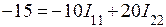
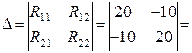
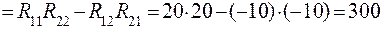
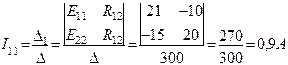 ,
,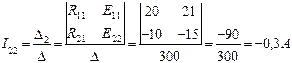 .
.
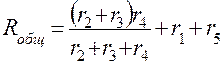 =
= 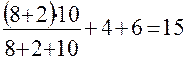 Ом
Ом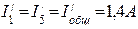 ;
; ;
;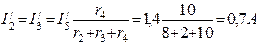
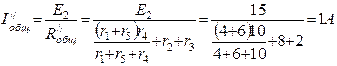 ;
;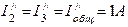 ;
;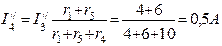 ;
;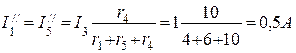 .
.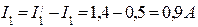 ;
;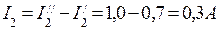 ;
;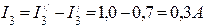 ;
;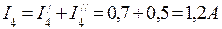 ;
;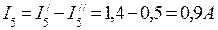 .
.
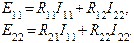
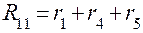 =4+10+6=20 Ом
=4+10+6=20 Ом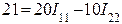
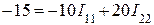
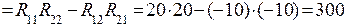
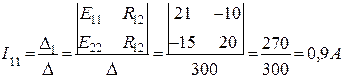 ,
,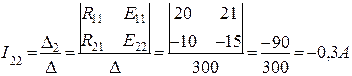 .
.
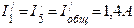 ;
;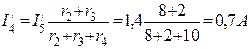 ;
;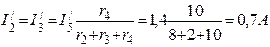
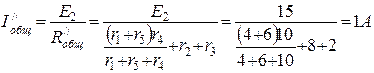 ;
;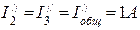 ;
;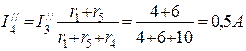 ;
;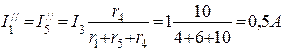 .
.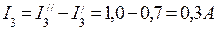 ;
;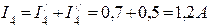 ;
;
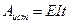 (1.34)
(1.34)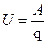 ,
, 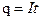 ,
, 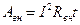 , то
, то 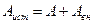 (1.35)
(1.35)
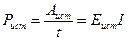 (1.36)
(1.36)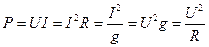 (1.37)
(1.37) (1.38)
(1.38)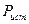 называется его коэффициентом полезного действия (КПД):
называется его коэффициентом полезного действия (КПД):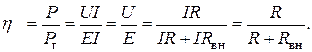 (1.39)
(1.39)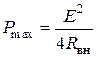 (1.40)
(1.40)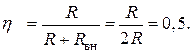
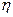 согл = 0,5, при холостом ходе
согл = 0,5, при холостом ходе 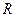 =
= 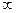 , а при коротком замыкании
, а при коротком замыкании 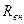 .
.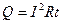 (1.41)
(1.41)


