
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема№5.Общие свойства четырёхполюсников.Содержание книги
Поиск на нашем сайте
При передачи электроэнергии от источника к потребителю используются различные передающие цепи: линии электропередач, трансформатор, фильтры и т.д. Эти промежуточные передаточные цепи объединяют одним общим названием четырёхполюсник. Он представляет собой устройство с двумя входными зажиганиями. В том случае, когда имеется источник энергии – активный А. Если нет, то пассивный П. Часто пассивный четырёхполюсник является передаточным звеном между источником энергии и нагрузкой, находящейся под воздействием U2. Полагая, что схема внутренних соединений его неизменна, и входящее R – линейно, можно составить соотношение между U1 и Y1, и U2 и Y2. Эти соотношения определяются так называемыми уровнями четырёхполюсника. U1=A U2 + B Y2 Y1=C U2 = D Y2
Величины А, В, С, D представляют собой комплексный коэффициент зависящий от внутренней схемы, параметров отдельных элементов схемы и частоты питающего напряжения. Очевидно, что в соответствии с написанным уравнением A и D = 0, B=R, C= проводимости. Связь: AD-DC=1 В том случае, когда перемена мест источника электроэнергии и нагрузки не вызывает изменений Y и A=D Последнее уравнение примет вид A2-BC=1. A,B,C,D определяется на основании опытов холостого хода и короткого замыкания. Если четырёхполюсник работает на переменной Y, то коэффициенты неизменные комплексные величины. Если на постоянном, то A,B,C,D – вещественные числа. При опыте x x сопротивление нагрузки считается равным, к зажимам 2 2’ подключается V, обладают высоким r. Измерив величины U1xx и Y1xx, P1xx со стороны входа что Y2xx – со стороны входа можно определить коэффициенты A, C из основного уравнения, учитывая что Y2xx=0. Из уравнения очевидно, что U1xx=A U2, а Y1xx=A U2, откуда A=U1xx/U2; C=Y1xx/U2. Входное сопротивление определяется: Z1xx=U1xx/Y1xx=A/C Угол сдвига фаз определяется:
При опыте k3 2-е напряжение считается равным 0. поэтому основное уравнение будет: U1k3=B Y2 B=U1k3/Y2 Y1k3=D Y2 D=Y1k3/Y2
При режиме л3 входное сопротивление определяется по формуле: Z1k3=U1k3/Y1k3=B/D Угол сдвига фаз между U и Y при л3:
Располагая числовыми значениями A,B,C,D можно определить выходные Y и U при любых заданных выходных величинах, и наоборот.
Напомним, что устройство, которое имеет два входных контакта, называют четырехполюсником. Четырехполюсник, в схеме которого отсутствует источники электрического питания, называют пассивным(трансформаторы, электрические фильтры, лимит передачи электрической энергии и т.д.), а если присутствуют источники питания –активным(усилители, мостовые схемы, если в одной из диагональных схем находится источник электрического питания и т.п.). Четырехполюсник, который содержит линейные элементы, называется линейным, а если он содержит нелинейные элементы, называется нелинейным или параметрическим. Напомним, что линейным элементом называется элемент, если его параметры не зависят от электрического токаи напряжения, а параметры нелинейного элемента зависят от тока и напряжения. Кроме того, четырехполюсники делятся на автономные (содержат независимые источники электрического питания) и неавтономные, которые имеют в своих схемах зависимые источники питания.
В электрических цепях четырехполюсники используются в качестве передаточных звеньев между источниками питания и нагрузкой. В этом случает полагают, что можно изменить нагрузку и напряжение на входе, а сама схема четырехполюсника и сопротивление его элементов остаются неизменными. Принципиально теория четырехполюсника заключается в том, что, используя некоторые параметры, можно связать между собой Рассмотрим линейный пассивный четырехполюсник, изображенный на рис 5.1:
Рис 5.1. (
Если заменить z источником ЭДС, внутреннее сопротивление которого равно нулю, то применяя принцип наложения можно считать, что действует в схеме только один источник, напряжение
Рис.5.2.
Тогда
Где
Если рассмотреть случай, когда действует в схеме четырехполюсника только U2, которое учитывает влияние нагрузки Z, а зажимы 1’ и 1 замкнуты накоротко (U1=0,рис 5.3) То
Где Y22 – выходная проводимость при коротком замыкании на входе Y12 – взаимная или передаточная приводимость(проводимость обратной связи)
Рис.5.3
Следует заметить, что Y21=Y12 согласно принципу обратимости и определяют токи во входном (или выходном) контуре четырехполюсника при заданном U в выходном (или входном) контуре и при одинаковом напряжении на входе и выходе
Проведя наложение схем рис 5.2 и рис 5.3 получают:
Уравнение (5.4) называют уравнением четырехполюсника с Y-параметрами(параметры короткого замыкания) При анализе четырехполюсники применяют так же уравнения с Н-параметрами (смешанные параметры). В этом случае независимые переменные U2 и I2 из системы уравнений (5.4) можно записать
где
Проводя аналогичные рассуждения можно получить другие формы уравнений четырехполюсника. Например, уравнение четырехполюсника с Z-параметрами(параметры холостого хода)
Следует заметить, что в данном случае известны (или заданы) токи (
А)
Б)
С)
Д)
Четырехполюсники в основном используются для систем, которые передают электрические сигналы. Чтобы проводить анализ сигналов через четырехполюсник следует рассмотреть функции четырехполюсника по направлению к току
Коэффициент передачи активной мощности
Комплексное входное сопротивление
Рассмотрим коэффициенты передачи четырехполюсника, например, при известных Y-параметрах. Если взять из системы уравнений (5.4) второе уравнение, а также закон Ома
где Y=1/z
Если использовать формулу для входной проводимости
и для уравнения системы (5.4) на
Если в схему рис 5.1 на место, где проходит ток но
где
Аналогичные расчеты можно сделать самостоятельно и получить при заданных z-параметрах четырехполюсника
Классификация фильтров. Фильтры нижних и верхних частот будут описаны в теме 8.
Тема №6.
|
||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 410; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.56.234 (0.011 с.) |

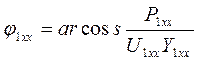

 на входе и выходе четырехполюсника, при этом не проводить расчетов
на входе и выходе четырехполюсника, при этом не проводить расчетов 
 -входной ток и напряжение,
-входной ток и напряжение,  -выходной ток и напряжение)
-выходной ток и напряжение) ,а зажимы
,а зажимы  - накоротко замкнуты, и
- накоротко замкнуты, и 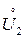 =0 (рис 5,2):
=0 (рис 5,2):
 (5.1)
(5.1) - входная проводимость при коротком замыкании на выходе,
- входная проводимость при коротком замыкании на выходе,  - передаточная проводимость (проводимость прямой передачи)
- передаточная проводимость (проводимость прямой передачи) (5.2)
(5.2)
 (5.3)
(5.3) (5.4)
(5.4) (5.5)
(5.5)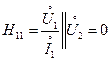 -входное сопротивление при коротком замыкании на выходе
-входное сопротивление при коротком замыкании на выходе -коэффициент обратной связи по напряжению или коэффициент обратной передачи напряжения при холостом ходе на входе
-коэффициент обратной связи по напряжению или коэффициент обратной передачи напряжения при холостом ходе на входе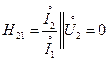 -коэффициент прямой передачи тока при коротком замыкании на входе
-коэффициент прямой передачи тока при коротком замыкании на входе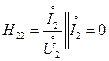 -входная проводимость при холостом ходу на входе.
-входная проводимость при холостом ходу на входе. (5.5)
(5.5) ),а
),а  являются сопротивлениями.
являются сопротивлениями. - входное сопротивление на холостом ходу на выходе
- входное сопротивление на холостом ходу на выходе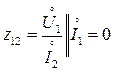 -сопротивление обратной связи
-сопротивление обратной связи -сопротивление прямой передачи
-сопротивление прямой передачи -выходные сопротивления пир холостом входе на входе
-выходные сопротивления пир холостом входе на входе ,
,  (5.6)
(5.6) (5.7)
(5.7) (5.8)
(5.8) (рис 5.1), то решая их совместно получают коэффициент передачи по напряжению
(рис 5.1), то решая их совместно получают коэффициент передачи по напряжению (5.9)
(5.9) (5.10)
(5.10) можно найти входную проводимость четырехполюсника
можно найти входную проводимость четырехполюсника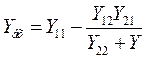 (5.11)
(5.11) -
-  ,
, (5.12)
(5.12)
 (5.13)
(5.13) (5.14)
(5.14)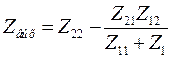 (5.15)
(5.15)


