Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Цепи с параллельным соединением ветвей.Содержание книги
Поиск на нашем сайте
Для расчета цепи с параллельным соединением ветвей применяется метод проводимостей. Рассмотрим применение этого метода на примере расчета цепи, показанной на рис.2. Нужно определить общий ток I в неразветвленной цепи. Он равен векторной сумме токов параллельных ветвей. При построении векторных диаграмм в случае параллельного соединения элементов в качестве исходного вектора используется вектор напряжения
Вектор тока Ī представляет собой сумму векторов тока ĪR1, который совпадает с вектором напряжения Ia = IR1 + IR2 + IR3 Реактивная составляющая тока цепи равна алгебраической сумме реактивных составляющих токов ветвей:
Векторную диаграмму токов на рис.14 можно преобразовать к виду, изображенному на рис.15.
Векторную диаграмму, показанную на рис.15, обычно называют треугольником токов. Ток в цепи до разветвления равен
Для нахождения активной, реактивной и полной проводимостей можно разделить модуль каждого вектора тока на модуль вектора
g – активная проводимость; b – реактивная проводимость; у – полная проводимость. В общем случае, если ветвь содержит не только одно сопротивление (R или L или C), но несколько (как ветви аб и гд на рис.2) значения проводимостей определяются следующим образом:
Считается, что емкостная проводимость bc положительна, так как ей соответствует опережающий по фазе напряжение емкостный ток, а индуктивная bL- отрицательна, так как ей соответствует индуктивный отстающий ток. В общем случае активная проводимость разветвления в целом равна арифметической сумме активных проводимостей ветвей:
а реактивная проводимость равна алгебраической сумме реактивных проводимостей:
Условно можно принять, что угол φ>0, если ток опережает напряжение. Следовательно, в общем виде закон Ома для параллельного соединения будет иметь вид I = уU,
В схемах с параллельным соединением ветвей может преобладать емкостная или индуктивная проводимость, но возможен и частный случай, когда
Это равенство является условием резонанса токов, при таком режиме реактивные токи в ветвях могут значительно превышать общий ток I, поступающий от источника. Векторную диаграмму токов можно изобразить на комплексной плоскости. Для цепи на рис.2 она будет иметь такой вид, как на рис.14 (см.рис.17).
Общий ток цепи равен сумме токов ветвей İ = İ1 + İ2 + İ3 + İ4
Исходя из написанного выше, можно записать выражение для общего тока: İ = (у1 + у2 + у3 +у4) Ů, İ = (g1 + g2 + g3 + j bC2 - j bL1 - j bL4) Ů,
Это соотношение есть закон Ома для параллельной цепи, записанный в комплексном виде. Сомножитель перед - полная проводимость параллельной цепи в комплексной форме Ток цепи Все комплексные величины можно записать в показательной форме. В общем случае Ψ – угол между напряжением и вещественной осью. У нас ψ = 0,. Комплекс проводимости в показательной форме
Комплекс тока в показательной форме
Резонанс в электрических цепях.
Рассмотренные выше электрические цепи представляют собой последовательный и параллельный колебательные контуры соответственно. Цепь, в которой индуктивность, емкость и активное сопротивление соединены последовательно, называется последовательным колебательным контуром. Цепь, в которой индуктивность, емкость и активное сопротивление соединены параллельно, называется параллельным колебательным контуром. В колебательных контурах при определенных условиях могут возникать особые явления, которые называют резонансными. Резонанс в последовательном колебательном контуре называют резонансом напряжений, резонанс в параллельном колебательном контуре – резонансом токов. В цепях переменного тока резонанс наступает тогда, когда частота источника напряжения равна резонансной частоте контура (собственной частоте колебаний контура, если
Резонанс напряжений.
Закон Ома для последовательной цепи, состоящей из активного, индуктивного и емкостного сопротивлений (си.рис.1), выражается формулой
где R – активное сопротивление контура; XL и XC - индуктивное и емкостное сопротивления контура соответственно. Угол сдвига фаз между током и напряжением
Резонанс наступает тогда, когда цепь ведет себя как чисто активная, т.е. когда ток и напряжение совпадают по фазе, угол φ = 0. Условием возникновения резонанса в последовательном колебательном контуре является равенство реактивных сопротивлений контура
Тогда полное сопротивление цепи будет равно его активной составляющей:
Сдвига фаз между током и напряжением не будет, угол φ = 0, cos φ = 1. Векторная диаграмма цепи при резонансе напряжений представлена рис. 18 (а и б).
При резонансе напряжений действующие значения реактивных составляющих напряжения UL и UC равны по величине, мгновенные значения равны и противоположны по знаку, векторы Результирующее напряжение при резонансе равно его активной составляющей U =Ua. Следовательно, мощность, развиваемая источником, является активной мощностью, она поддерживает в цепи R, L, C незатухающие колебания, несмотря на то, что в цепи есть активное сопротивление. Энергия магнитного поля при резонансе полностью переходит в энергию электрического поля и наоборот:
Частота, при которой в контуре наступает резонанс, называется резонансной. Значение резонансной частоты можно определить из условия резонанса XL=XC. Т.к. то резонансная частота контура
Резонанс напряжений можно получить изменяя в цепи индуктивность, емкость или частоту напряжения источника питания контура, всего, если хотят настроить контур в резонанс, используют конденсатор переменной емкости. С этого конденсатора снимают выходное напряжение. Если XL=XC>=R, напряжение на индуктивности UL и емкости UC могут достигать значительной величины и во много раз превышать общее напряжение U, приложенное к цепи. Ток в цепи I также значительно возрастает: а) Характеристическое сопротивление контура (или волновое)
Эта величина имеет размерность сопротивления (величину ρ можно получить из уравнения (х) ). б) Добротность контура Добротность контура служит характеристикой реального контура, когда При резонансе добротность контура равна отношению напряжения на емкости или индуктивности к напряжению на активном сопротивлении. Покажем это:
Т.к.
Отсюда
Добротность радиотехнических контуров обычно составляет 50-200.
в) Затухание контура г) Резонансные кривые – это графическое изображение зависимости напряжений на емкости, индуктивности и активном сопротивлении, а также тока от частоты (см.рис.19).
Чаще всего резонансные кривые стоят в зависимости от относительной частоты
где А – значение напряжения или тока; w, f - текущее значение угловой частоты и частоты соответственно;
Построенные таким образом зависимости обладают наибольшей общностью. Вид резонансных кривых, построенных в функции относительной частоты, целиком определяется добротностью контура Q. На рис.20 показано семейство резонансных кривых
Из рис.20 видно, что с увеличением добротности контура резонансная кривая становится острее. д) Полоса пропускания контура (или ширина резонансной кривой) – это полоса частот вблизи резонанса, на границах которой выходная величина А (напряжение, ток) составляет
Резонанс токов. Как указывалось выше, резонанс токов наблюдается в параллельных колебательных контурах, содержащих элементы L, C и R (см.рис.22). Параллельные контуры могут быть и другого вида.
Примечание: Rогр включают для исключения перегрузки источника питания. Закон Ома для параллельного соединения активного сопротивления, емкости, индуктивности в общем случае выражается формулой:
где g - активная проводимость; bL и bc - реактивные проводимости, индуктивная и емкостная соответственно. Угол сдвига фаз между током в неразветвленной части цепи I и приложенным напряжением равен
Если bL = bc, цепь будет вести себя так, будто она содержит только активное сопротивление. В этом случае в неразветвленной части цепи ток I будет совпадать по фазе с приложенным к контуру напряжением, φ = 0, cosφ = 1.Такое состояние цепи называется резонансом токов. Резонансная частота контура определяется следующим образом
Т.к. при резонансе
Отсюда
Или
При малых значениях активных сопротивлений R1 и R2 выражение для f рез для последовательного колебательного контура
Векторная диаграмма цепи для случая, когда
Общий реактивный ток, равный разности реактивных токов ветвей, при резонансе токов равен 0. Общий ток цепи имеет только активную составляющую, таким образом, его величина в момент резонанса имеет наименьшее значение. В идеальном случае, если R1 = R2 = 0, резонанс токов эквивалентен размыканию цепи. Рассмотрим, какое значение имеют токи в ветвях и индуктивностью и емкостью при резонансе, если активное сопротивление ветвей контура R1 и R2 малы, по сравнению с реактивными сопротивлениями. Ток Ī1 отстает, а ток Ī2 опережает напряжение
В этом случае токи Ī1 и Ī2 между собой сдвинуты по фазе на угол, близкий к π, а амплитуды их будут практически равны, т.к. ХL = Хc, и во много раз больше амплитуды тока в неразветвленной ветви. Поэтому резонанс в параллельных контурах называют резонансом токов. Поскольку токи ветвей сдвинуты по фазе на угол ≈ π при малых R1 и R2 и равны по величине, можно считать, что при резонансе они образуют как бы один контурный ток Ir, замыкающийся в колебательном контуре. Зависимость тока Iк от частоты ƒ показана на рис.25 (резонансная кривая). Свойства параллельного колебательного контура характеризуются теми же величинами, что и последовательный колебательный контур. Добротность Q = ρ ⁄ R для параллельного контура равна отношению тока в индуктивности Il или емкости Iс к току в неразветвленной части цепи при резонансе
Резонансные кривые для параллельного колебательного контура показаны на рис.26. (R≈0).
Резонанс токов в отличие от резонанса напряжений не является опасным для электрических установок, поскольку в реальных условиях реактивные проводимости редко бывают высокими. Явления резонанса напряжений и токов широко используются в технике связи, автоматике и телемеханике, для улучшения cosφ в промышленных установках. Путем настройки колебательного контура в резонанс с частотой передаваемого сигнала можно выделить полезный сигнал.
|
||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 1756; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.111.3 (0.009 с.) |

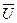 , так как напряжение в этом случае одно и то же для всех ветвей (см.рис.14).
, так как напряжение в этом случае одно и то же для всех ветвей (см.рис.14).
 , отстающего от вектора напряжения
, отстающего от вектора напряжения  равен сумме векторов тока
равен сумме векторов тока  , совпадающего с вектором напряжения
, совпадающего с вектором напряжения  , опережающего
, опережающего  отстает от
отстает от  IP = IC – IL1 – IL4 (cкалярные величины).
IP = IC – IL1 – IL4 (cкалярные величины).

 ;
;  ;
; ;
;  ;
; ;
;  ;
; .
. ,
,

 U.
U.


 , где
, где  .
. , где
, где
 , где
, где 
 , где
, где 


 , где
, где ,
, 

 ). При резонансе ток и напряжение совпадают по фазе, т.е. угол φ = 0.
). При резонансе ток и напряжение совпадают по фазе, т.е. угол φ = 0.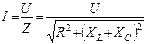

 .
.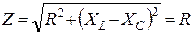

 и
и  равны и противоположны по знаку.
равны и противоположны по знаку.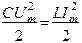
 и
и  ,
,
 . Для исключения перегрузки источника питания в схему иногда вводят ограничивающее сопротивление Rорг . Поскольку резонанс сопровождается значительными перенапряжениями и сверхтоками, в мощных установках он является аварийным. Свойства колебательного контура характеризуются рядом величин:
. Для исключения перегрузки источника питания в схему иногда вводят ограничивающее сопротивление Rорг . Поскольку резонанс сопровождается значительными перенапряжениями и сверхтоками, в мощных установках он является аварийным. Свойства колебательного контура характеризуются рядом величин: .
.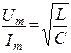 ).
).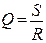
 .
. , но
, но 
 , то
, то  и
и 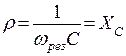
 и
и 



 - значения угловой частоты и частоты при резонансе.
- значения угловой частоты и частоты при резонансе. для различных значений добротности контура.
для различных значений добротности контура.
 от резонансного (максимального) значения (см.рис.21).
от резонансного (максимального) значения (см.рис.21).

 ,
,


 ,
, 


 показана на рис.23 (значения величин взяты произвольно).
показана на рис.23 (значения величин взяты произвольно).
 и ток Ī на угол, близкий к π⁄2 (см.рис.24).
и ток Ī на угол, близкий к π⁄2 (см.рис.24).