
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Электротехники и электроникиСодержание книги
Поиск на нашем сайте
Статистики и информатики
Проф. Цуркин А.П. Преподаватель Мосолов Д.Н. Каф.АСОИиУ Учебное пособие по курсу Электротехники и электроники Москва 2008г. Содержание: Тема №1. Введение Тема №2. Электрическое поле. Электрические цепи постоянного тока Тема №3. Магнитное поле. Магнитные цепи. Индуктивность и ёмкость в электрических цепях Тема №4. Однофазные электрические цепи синусоидального тока Тема №5. Общие свойства четырёхполюсников Тема №6. Переходные процессы в электрических цепях Тема №7. Методы расчётов переходных процессов Тема №8. Трёхфазные электрические цепи Тема №9. Периодические и апериодические несинусоидальные сигналы Тема №10. Расчёт электрических цепей с помощью оператора Лапласа Тема №11. Основы теории электромагнитного поля Тема 12. Основы теории электронных приборов Тема 13. Транзисторные усилители электрических сигналов Тема 14. Аналоговые и цифровые элементы и устройства Тема 15. Комбинационные цифровые устройства Тема 16. Источники вторичные питания Генераторы Раздел 1-ЭЛЕКТРОТЕХНИКА. Тема №1. Введение.
Целью курса по "Электротехнике и электронике" является овладение основами теоретических и практических знаний в области электротехники и электроники. Без знания основных законов электротехники и электроники, принципов работы электротехнических устройств и электронных приборов невозможно овладеть избранной профессией и стать полноценным инженером. Помимо того, следует иметь в виду, что электротехника и электроника являются теоретической базой для ряда других дисциплин, а именно автоматики, вычислительной техники, технологического оборудования и т. п. Теоретические методы, которые разработаны в электротехнике иэлектронике с успехом применяются и в других инженерных дисциплинах. Основные задачи курса заключается в освоении базовых понятий, определений и методов в области электротехники и электронике, которые обеспечивали бы успешное освоение специальных электротехнических дисциплин и дисциплин по элетронике на последующих стадиях обучения.
Простые и сложные цепи. Цепи бывают простые и сложные. Простыми электрическими цепями называют цепи, содержащие одни источник энергии. Цепь, содержащая два и более источника, называется сложной. Кроме того участок цепи, содержащий источник электрической энергии, принято называть активным А, не содержащий — пассивным П. Участок электрической цепи, по которому проходит ток одного и того же значения и направления, называют ветвью. Место соединения трех и более ветвей называют узлом. Узел электрической цепи на схеме отмечают жирной точкой. Если на схеме место скрещивания ветвей точкой не отмечено, это означает, что электрического соединения между ними в месте их пересечения нет. Замкнутую электрическую цепь, образуемую одной или несколькими ветвями, называют контуром. Контур, внутри которого не лежат другие ветви, связывающие между собой его узлы, называют простыми.
Тема №2.Электрическое поле.Электрические цепи постоянного тока.
Метод контурных токов
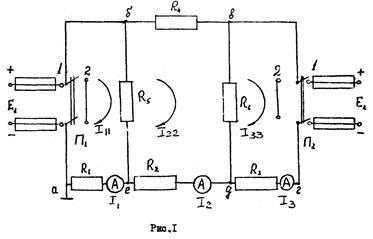
Этот метод расчета основан на том, что действительный (истинный) ток в любой ветви, входящей в несколько контуров (например, на рис.1 ветвь с сопротивлением R5 входит в контур абе и в контур бвде), можно представить в виде алгебраической суммы токов, каждый из которых замыкается по своему контуру.
Исходя из этого, сложную цепь можно разбить на ряд контуров и считать, что в каждой ветви данного контура протекает одинаковый ток. Этот ток называют контурным. Направление его выбирают произвольно. Контурные токи и будут теми неизвестными, которые нужно определить. Зная значения и направления контурных токов, можно определить действительный ток в каждой ветви цепи: a) ток в ветви, входящий в данный контур, равен контурному току; b) ток в ветви, входящий в несколько контуров, равен алгебраической сумме контурных токов. Как определить контурные токи? Для каждого контура составляют уравнения по второму закону Кирхгофа, причем при составлении уравнений контур обходят по направлению контурного тока. При этом необходимо учитывать падение напряжения в смежной с другим контуром ветви от контурного тока смежного контура. Это падение напряжения будет положительным, если направление контурного тока в смежном контуре совпадает с направлением обхода данного контура и отрицательным, если направление контурного тока не совпадает с направлением обхода. Значение э.д.с. берется со знаком плюс, если направление обхода контура совпадает с направлением действия э.д.с., и со знаком минус – если не совпадает. При выборе контуров руководствуются следующим:
N=b-y+1 (1.33) где b – число ветвей; y – число узлов;
На примере расчета цепи, представленной на рис.1, поясним сказанное выше.
1-й контур – I11, 2-й контур – I22, 3-й контур – I33.
1-й контур:
2-й контур:
= (1) 3-й контур:
I1=I11, I2=I22, I3=I33, I4=I22, I5=I11-I22, I6=I22-I33. Для решения системы уравнений, составленной по второму закону Кирхгофа, целесообразно применить метод определителей. Тогда в общем виде эта система уравнений записывается следующим образом:
и т.д. Поясним смысл каждого члена уравнений. a) В левой части каждого уравнения стоят суммарные значения э.д.с., входящие в контур. Они имеют знак плюс, если направление обхода контура и направление действия суммарной э.д.с. совпадают. Для цепи на рис.1: E11=E1, E22=0, E33=-E2 b) Сопротивление R11, R22, R33 – собственные сопротивления I, II, III контуров соответственно. Собственные сопротивления контуров для цепи на рис.1: R11=R1+R5, R22=R2+R5+R4+R6, R33=R3+R6 c) Сопротивления R12, R21, R13, R31 и т.п. – общие или смежные сопротивления контуров. Смежное (общее) сопротивление представляет собой сопротивление ветви, входящей в несколько контуров. Его обозначают с индексом, состоящим из номеров контуров, в которые входит ветвь. Для цепи на рис.1 смежные сопротивления: для I контура R12, для II контура R21, для II контура R23, для III контура R32. Если через общее сопротивление контурные токи смежных контуров протекают в разных направлениях, в уравнение (2) такое общее сопротивление ставится со знаком минус. В цепи на рис.1 через все смежные сопротивления токи текут в разных направлениях и в этом случае принимают, что R12=R21=-R5; R23=R23=-R6. Для составления определителя необходимо, чтобы все уравнения имели одинаковое число членов. В правую часть каждого уравнения записываются произведения всех контурных токов на соответствующие сопротивления, а в случае, если это сопротивление не входит в рассматриваемый контур, его принимают равным нулю. Составим уравнения для 3-х контуров на рис.1, учитывая сделанные замечания.
Если в эти уравнения поставить значения каждого члена и учесть сказанное о знаках, получим уравнение (1). Покажем, как решается система уравнений (2) методом определителей. Ток К-го контура равен
где
Каждый частный определитель Например, если определяется ток I – го контура, частный определитель будет иметь вид
При расчете цепи методом контурных токов можно не составлять уравнения по 2 – ому закону Кирхгофа, а достаточно составить определители по уравнениям (5), (6) и по уравнению (5) рассчитать контурные токи. При составлении определителей нельзя забывать о знаках перед членами определителя (перед э.д.с. ставят знак минус, если направление обхода и направление действия э.д.с. не совпадают, перед общими сопротивлениями ставят знак минус, если контурные токи тех контуров, в которые входят эти сопротивления, направлены в разные стороны).
Метод наложения
Метод наложения основан на принципе независимости действия э.д.с. Согласно этому принципу токи, протекающие в цепи при наличии нескольких э.д.с., можно представить как алгебраическую сумму токов, создаваемых каждой из э.д.с. в отдельности. Вначале определяются значения токов в ветвях, создаваемых действием только одного источника (например, для рис.1 I1, I2, I3, I4, I5, I6 от Е1, полагая Е2=0). Затем таким же образом определяют токи в ветвях, создаваемые действием другого источника (например, для рис.1 токи I1//, I2//, I3//, I4//, I5//, I6// от Е2, полагая Е1=0). Затем находятся действительные токи в ветвях, как алгебраические суммы токов, создаваемые в одних и тех же ветвях отдельными источниками. Рассмотрим порядок определения токов, создаваемых отдельными э.д.с. на примере схемы рис.1. Вначале находятся токи в ветвях и их направления при действии только одной э.д.с., например, Е1, когда Е2=0. Для этого определяется общее сопротивление цепи R/общ (внутренним сопротивлением источника э.д.с. Е2 пренебрегаем).
После этого определяются токи в ветвях схемы рис.1 при действии только э.д.с. Е1, а именно:
Затем составляется схема рис.1 при действии Е2 (Е1=0, внутреннее сопротивление источника э.д.с. пренебрегаем) и наносятся направления токов I1//, I2//, I3//, I4//, I5//, I6//. Аналогично вышеизложенному рассчитываются токи, создаваемые действием источника Е2. Действительные токи в ветвях определяются как алгебраическая сумма составляющих токов, проходящих через соответствующие ветви:
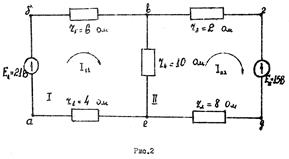
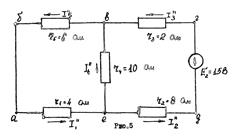
Составляется третья схема, на которой наносится направления действительных токов. Направление действительных токов в ветвях выбирается по большему составляющему току в каждой цепи. Пример расчета линейной цепи методом контурных токов. Найти токи в схеме рис.2. Численные значения сопротивлений и э.д.с. указаны на рисунке.
Решение. В этой схеме два независимых контура I и II (N=3-2+1). Выбираем произвольно направление контурных токов I11 и II22 по часовой стрелке. Система уравнений согласно второму закону Кирхгофа для данной цепи запишется в следующем виде:
Определяем собственные сопротивления контуров:
Сопротивление смежной ветви R12=R21=-r4. Внутренними сопротивлениями источников пренебрегаем. Контурные э.д.с. равны: E11=E1=21 B, E22=-E2=-15 B. Перед э.д.с. E2 знак минус, так как направление обхода контура не совпадает с положительным направлением действия э.д.с. При составлении уравнения по второму закону Кирхгофа направление обхода контуров принимаем совпадающим с направлением контурных токов. В соответствии с численными значениями, полученными для R11, R12, R21, R22, E11 и E22, с учетом знаков уравнения перепишутся следующим образом:
Главный определитель системы
Контурные токи I11 и I22 будут равны:
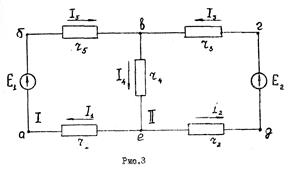
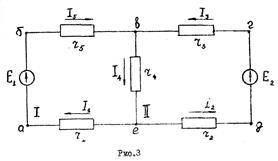
После подсчета контурных токов определяются действительные токи в ветвях: I1=I5=I11=0,9A; I2=I3=I22=-0,3A; I4=I11-I22=1,2A Значение контурного тока I22 получилось отрицательным, поэтому истинное направление его будет обратным принятому на рис.2. Истинные направления токов во всех ветвях показаны стрелками на рис.3.
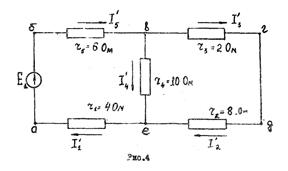
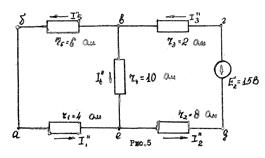
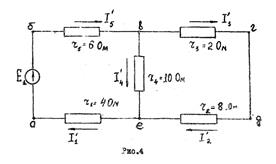
Пример расчета линейной цепи методом наложения. Найти этим методом токи в ветвях схемы рис.2. Решение. Исключаем из схемы э.д.с. E2. При действии в схеме рис.2 одной э.д.с. E1 примем, что токи будут иметь направления, как указано на рис.4.
Для схемы рис.4 находим общее сопротивление цепи (внутреннее сопротивление источников э.д.с. E1 и E2 принимаем равными нулю).
Затем находим токи в ветвях схемы рис.4 от действий только э.д.с. E1.
Полагая э.д.с. E1=0, находим направления и значения токов в ветвях схемы от действия э.д.с. E2.
Действительные токи в ветвях определяются алгебраическим сложением составляющих токов ветвей. Направления действительных токов в ветвях определяются по большей составляющей тока каждой ветви. Итак, для схемы рис.2 действительные токи в ветвях будут равны:
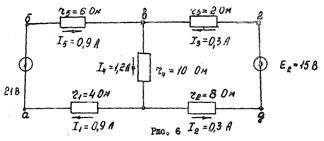
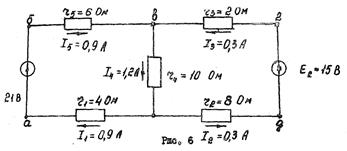
Таким образом, накладывая схему рис.4 на схему рис.5 получим схему рис.6 с действительными значениями и направлениями токов в ветвях при одновременном действии двух источников э.д.с E1 и E2.
Следует отметить, что при расчете более сложной электрической цепи, общее сопротивление эквивалентной схеме более удобно определить, разбивая всю схему, начиная со стороны противоположной действию источника э.д.с., на ряд участков, заключенных между соответствующими узлами.
Решение. В этой схеме два независимых контура I и II (N=3-2+1). Выбираем произвольно направление контурных токов I11 и II22 по часовой стрелке. Система уравнений согласно второму закону Кирхгофа для данной цепи запишется в следующем виде:
Определяем собственные сопротивления контуров:
Сопротивление смежной ветви R12=R21=-r4. Внутренними сопротивлениями источников пренебрегаем. Контурные э.д.с. равны: E11=E1=21 B, E22=-E2=-15 B. Перед э.д.с. E2 знак минус, так как направление обхода контура не совпадает с положительным направлением действия э.д.с. При составлении уравнения по второму закону Кирхгофа направление обхода контуров принимаем совпадающим с направлением контурных токов. В соответствии с численными значениями, полученными для R11, R12, R21, R22, E11 и E22, с учетом знаков уравнения перепишутся следующим образом:
Главный определитель системы
Контурные токи I11 и I22 будут равны:
После подсчета контурных токов определяются действительные токи в ветвях:
I1=I5=I11=0,9A; I2=I3=I22=-0,3A; I4=I11-I22=1,2A Значение контурного тока I22 получилось отрицательным, поэтому истинное направление его будет обратным принятому на рис.2. Истинные направления токов во всех ветвях показаны стрелками на рис.3.
Пример расчета линейной цепи методом наложения. Найти этим методом токи в ветвях схемы рис.2. Решение. Исключаем из схемы э.д.с. E2. При действии в схеме рис.2 одной э.д.с. E1 примем, что токи будут иметь направления, как указано на рис.4.
Для схемы рис.4 находим общее сопротивление цепи (внутреннее сопротивление источников э.д.с. E1 и E2 принимаем равными нулю).
Затем находим токи в ветвях схемы рис.4 от действий только э.д.с. E1.
Полагая э.д.с. E1=0, находим направления и значения токов в ветвях схемы от действия э.д.с. E2.
Действительные токи в ветвях определяются алгебраическим сложением составляющих токов ветвей. Направления действительных токов в ветвях определяются по большей составляющей тока каждой ветви. Итак, для схемы рис.2 действительные токи в ветвях будут равны:
Таким образом, накладывая схему рис.4 на схему рис.5 получим схему рис.6 с действительными значениями и направлениями токов в ветвях при одновременном действии двух источников э.д.с E1 и E2.
Следует отметить, что при расчете более сложной электрической цепи, общее сопротивление эквивалентной схеме более удобно определить, разбивая всю схему, начиная со стороны противоположной действию источника э.д.с., на ряд участков, заключенных между соответствующими узлами.
Активные и пассивные двухполюсники.
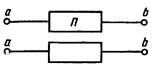
Двухполюсником называется часть сложной электрической цепи, которая имеет два зажима (входной и выходной), называемых полюсами. Двухполюсники бывают пассивные и активные. Двухполюсник, не содержащий источника энергии, называется пассивным. Линейным пассивный двухполюсник будет и тогда, когда в нем будут содержаться источники энергии, э. д. с. которых взаимно компенсируются, т. е. направлены навстречу друг другу и равны по значению. Двухполюсники условно изображают в виде прямоугольника, при этом для обозначения пассивного двухполюсника в прямоугольнике либо ставят букву П, либо не ставят никакой буквы (рис.).
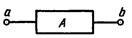
В схеме некомпенсированные двухполюсники, в которых содержатся источники электрической энергии, называются активными (рис.). В этом случае при обозначении двухполюсника в прямоугольнике ставят букву А.
При анализе электрической цепи, в которую входит пассивный двухполюсник, достаточно знать его характеристику. Так как пассивный двухполюсник является потребителем энергии, то в качестве характеристики можно взять его сопротивление, которое в этом случае называется внутренним или входным. Следовательно, на схеме замещения пассивный двухполюсник можно представить в виде одного элемента с сопротивлением, равным входному сопротивлению двухполюсника. Для активного двухполюсника наряду с сопротивлением важной характеристикой является внешняя, или вольт-амперная, характеристика, которая полностью определяет его свойства.
Электрическая энергия и работа. Мощность электрической цепи.
Работа источника электрического тока определяется по формуле:
Так как Работа и энергия – понятия равноценные. Энергия – способность источника совершать работу. Чтобы измерить энергию источника, надо измерить работу, которую он совершает, расходуя эту энергию. Измеряется энергия и работа в Джоулях (Дж). На практике за единицу энергии принимают 1 кВт·ч = 3600000 Дж. Электрическая мощность – это физическая величина, характеризующая быстроту передачи или преобразования электрической энергии:
Измеряется мощность в ваттах (Вт). Мощность, отдаваемая (полезная) источником энергии потребителю (приемнику)
Потери мощности во внутреннем сопротивлении
Условие передачи в нагрузку максимальной мощности.
Отношение мощности приемника (полезной мощности) к мощности источника энергии
Источник ЭДС развивает максимальную полезную мощность, когда внешнее сопротивление равно внутреннему сопротивлению источника:
Такой режим является невыгодным, так как 50 % энергии теряется во внутреннем сопротивлении источника
Режим цепи, при котором внешнее сопротивление цепи равно внутреннему сопротивлению источника энергии, называется режимом согласованной нагрузки. При согласованном режиме
Закон Джоуля-Ленца.
При протекании электрического тока по проводникам происходит преобразование электрической энергии в тепловую. Эта зависимость выражается формулой получившей название закон Джоуля-Ленца:
Q — количество тепла, выделенного в проводнике. Количество тепла Q измеряется иногда внесистемной единицей — калорией. 1 кал = 4,187 Дж. Отсюда, 1 Дж = 0,24кал.
Тема №3. Тема №4. Векторные диаграммы.
При расчете цепей переменного тока часто приходится суммировать (или вычитать) несколько однородных синусоидально изменяющихся величин одной и той же частоты ƒ, но имеющих разные амплитуды (Im, Em, Um) и начальные фазы (α, α1, α2). Такую задачу можно решать аналитическим путем тригонометрических преобразований или геометрически. Геометрический метод более прост и нагляден, чем аналитический. Синусоидальную величину (например, u = Um sin (wt + α)) изображают в виде радиуса-вектора
α – угол, образованный Пусть необходимо сложить две синусоидальные функции с одинаковым периодом, но разными начальными фазами (см.рис.4): U = Um1 sin (ωt + α1) и U2 = Um2 sin (ωt + α2).
Рис.4 По известному правилу сложения векторов можно получить вектор Вместо того, чтобы вращать векторы с угловой скоростью, можно предположить, что они неподвижны, а оси координат вращаются с угловой скоростью ω. На рис.4 изображено относительное расположение векторов и осей в момент t = 0. Геометрическое построение, описанное выше, определяет амплитуду ОМ =Um, фазу α и тем самым позволяет найти выражение Umsin(ωt + α) = Um1sin(ωt + α1) + Um2sin(ωt + α2), причем амплитуда Um будет равна
фаза α может быть определена через tg α
Аналогично линейная комбинация нескольких синусоидальных функций времени и той же частоты есть синусоидальная функция времени той же частоты:
Часто нужно вычислять производную или интегралы синусоидальных функций времени типа U(t) = Umsin(ωt + α). Имеем
Производные и первообразные от функции U (t) изображаются векторами, повернутыми к исходному вектору соответственно на углы + Изложенное выше применимо в тех случаях, когда требуется произвести сложение, дифференцирование, интегрирование синусоидальных напряжений и токов, либо линейные комбинации этих операций. Но это не применимо, если нужно подвергнуть напряжения или токи нелинейным алгебраическим операциям, как, например, умножению или возведению в степень. При таких операциях возникают круговые частоты, отличные от ω. Это обрекает на неудачу векторное построение, изображенное на рис.4. Построение векторов, изображенное на рис.4, называется векторной диаграммой. Обычно при построении векторных диаграмм вместо амплитудных значений синусоидальных величин берут их действующие значения. Действующие значения переменного напряжения и тока будут равны: Посредством действующих значений напряжения и тока проще выражается активная мощность. Активная мощность является основной величиной, характеризующей энергетические условия в цепи. Если для любого участка цепи известны векторы, длины которых равны действующим значениям напряжения U и тока I, то активная мощность есть скалярное произведение этих векторов:
Здесь φ – угол между векторами напряжения и тока. Для электрических расчетов применяют также две вспомогательные величины: полную мощность S = U I, ВА; реактивную мощность Q = U I sin φ, вар. Величины Р, Q, S соотносятся как стороны прямоугольного треугольника. Прямоугольный треугольник, стороны которого численно равны величинам Р, Q, S, называется треугольником мощностей (рис.5).
Резонанс напряжений.
Закон Ома для последовательной цепи, состоящей из активного, индуктивного и емкостного сопротивлений (си.рис.1), выражается формулой
где R – активное сопротивление контура; XL и XC - индуктивное и емкостное сопротивления контура соответственно. Угол сдвига фаз между током и напряжением
Резонанс наступает тогда, когда цепь ведет себя как чисто активная, т.е. когда ток и напряжение совпадают по фазе, угол φ = 0. Условием возникновения резонанса в последовательном колебательном контуре является равенство реактивных сопротивлений контура
Тогда полное сопротивление цепи будет равно его активной составляющей:
Сдвига фаз между током и напряжением не будет, угол φ = 0, cos φ = 1. Векторная диаграмма цепи при резонансе напряжений представлена рис. 18 (а и б).
При резонансе напряжений действующие значения реактивных составляющих напряжения UL и UC равны по величине, мгновенные значения равны и противоположны по знаку, векторы Результирующее напряжение при резонансе равно его активной составляющей U =Ua. Следовательно, мощность, развиваемая источником, является активной мощностью, она поддерживает в цепи R, L, C незатухающие колебания, несмотря на то, что в цепи есть активное сопротивление. Энергия магнитного поля при резонансе полностью переходит в энергию электрического поля и наоборот:
Частота, при которой в контуре наступает резонанс, называется резонансной. Значение резонансной частоты можно определить из условия резонанса XL=XC. Т.к. то резонансная частота контура
Резонанс напряжений можно получить изменяя в цепи индуктивность, емкость или частоту напряжения источника питания контура, всего, если хотят настроить контур в резонанс, используют конденсатор переменной емкости. С этого конденсатора снимают выходное напряжение. Если XL=XC>=R, напряжение на индуктивности UL и емкости UC могут достигать значительной величины и во много раз превышать общее напряжение U, приложенное к цепи. Ток в цепи I также значительно возрастает: а) Характеристическое сопротивление контура (или волновое)
Эта величина имеет размерность сопротивления (величину ρ можно получить из уравнения (х) ). б) Добротность контура Добротность контура служит характеристикой реального контура, когда При рез
|
||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 322; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.141.251 (0.018 с.) |

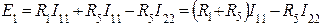
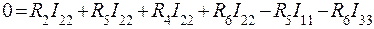 =
=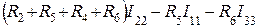
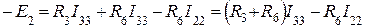
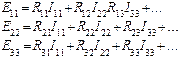 (2)
(2)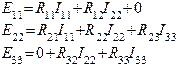 (3)
(3)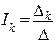 (4)
(4)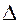 - главный определитель (детерминант);
- главный определитель (детерминант);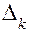 - частный определитель К – го столбца
- частный определитель К – го столбца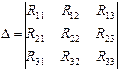 (5)
(5)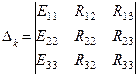 (6)
(6)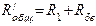 ;
; 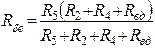 ;
; 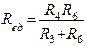
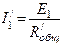 ;
; ;
;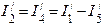 ;
;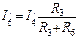 ;
;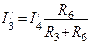 .
.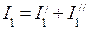 ;
; 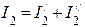 и т.д.
и т.д.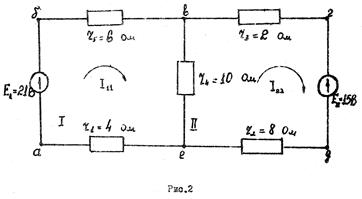

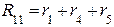 =4+10+6=20 Ом
=4+10+6=20 Ом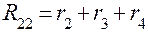 =8+2+10=20 Ом
=8+2+10=20 Ом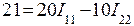
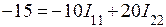
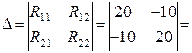
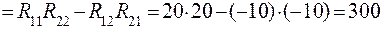
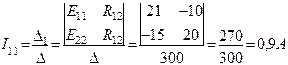 ,
,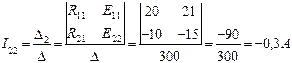 .
.
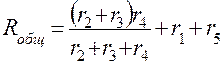 =
= 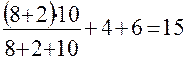 Ом
Ом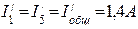 ;
; ;
;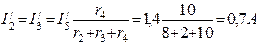
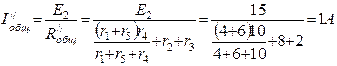 ;
;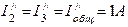 ;
;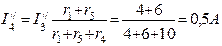 ;
;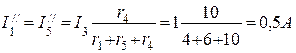 .
.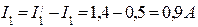 ;
;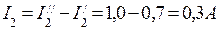 ;
;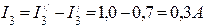 ;
;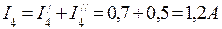 ;
;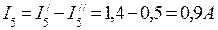 .
.
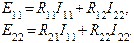
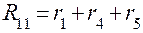 =4+10+6=20 Ом
=4+10+6=20 Ом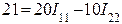
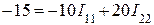
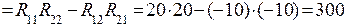
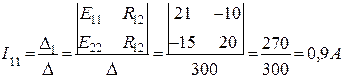 ,
,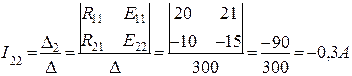 .
.
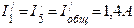 ;
;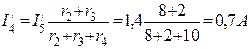 ;
;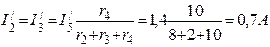
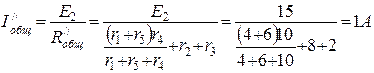 ;
;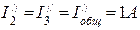 ;
;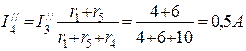 ;
;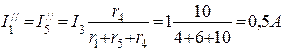 .
.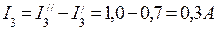 ;
;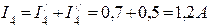 ;
;
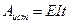 (1.34)
(1.34)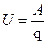 ,
, 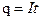 ,
, 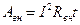 , то
, то 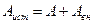 (1.35)
(1.35)
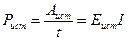 (1.36)
(1.36)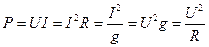 (1.37)
(1.37) (1.38)
(1.38)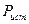 называется его коэффициентом полезного действия (КПД):
называется его коэффициентом полезного действия (КПД):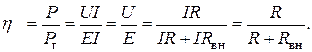 (1.39)
(1.39)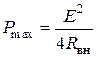 (1.40)
(1.40)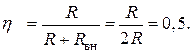
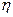 согл = 0,5, при холостом ходе
согл = 0,5, при холостом ходе 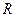 =
= 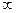 , а при коротком замыкании
, а при коротком замыкании 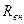 .
.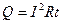 (1.41)
(1.41) с декартовыми координатами х=а, у=в (см. рис.3).
с декартовыми координатами х=а, у=в (см. рис.3).

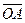 с осью Х в начальный момент времени, называемый начальной фазой. Вектор
с осью Х в начальный момент времени, называемый начальной фазой. Вектор 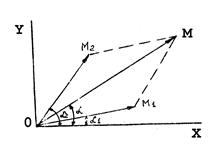
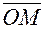 , изображающий сумму обеих функций U1(t) и U2(t), как геометрическую сумму векторов
, изображающий сумму обеих функций U1(t) и U2(t), как геометрическую сумму векторов  , изображающих эти функции. Все три векторы вращаются одновременно с угловой скоростью ω и легко непосредственно проверить, что ордината точки М представляет собой сумму функций Um1sin(ωt + α1) и Um2sin(ωt + α2). Аналогично абсцисса точки М равна сумме функций Um1cos(ωt + α1) и Um2cos(ωt + α2).
, изображающих эти функции. Все три векторы вращаются одновременно с угловой скоростью ω и легко непосредственно проверить, что ордината точки М представляет собой сумму функций Um1sin(ωt + α1) и Um2sin(ωt + α2). Аналогично абсцисса точки М равна сумме функций Um1cos(ωt + α1) и Um2cos(ωt + α2). ,
, .
.

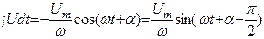 .
. и -
и - 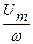 .
. , Вт.
, Вт.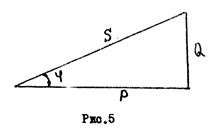
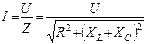

 .
.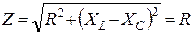

 и
и  равны и противоположны по знаку.
равны и противоположны по знаку.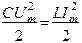
 и
и  ,
,
 . Для исключения перегрузки источника питания в схему иногда вводят ограничивающее сопротивление Rорг . Поскольку резонанс сопровождается значительными перенапряжениями и сверхтоками, в мощных установках он является аварийным. Свойства колебательного контура характеризуются рядом величин:
. Для исключения перегрузки источника питания в схему иногда вводят ограничивающее сопротивление Rорг . Поскольку резонанс сопровождается значительными перенапряжениями и сверхтоками, в мощных установках он является аварийным. Свойства колебательного контура характеризуются рядом величин: .
.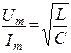 ).
).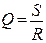
 .
.


