
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Какому знаку подчиняется сигнал на выходные цепи (вывод формулы)Содержание книги
Поиск на нашем сайте
А) Дифференц. RC Диф.цепь – это линейный четырёхпомостник, у которого выходное и пропорц. производной от входного. Uвых=
Учитывая, что ic проходит через сопр-е, для Uвых можно записать
Uвых = icR Uвых =
Из схемы видно, что Uc = Uвх=Uвых Учитывая что Uвых «Uвх Уравнение Uвых = Uвых = СR С=RС
2. Прохождение через линейные формирующие цепи с т.з. переходом процессов. А) диф. RC 3 С = tu Если tu = 3с то за время действия входного импульса (tu = t2 – t1) Конд. Почти полностью зарядится и в момент t2, когда действие импульса закончится Uвх = 0, напр-е на конд. Uc станет равен Uu (на рисунке пунктиром), а напр-е на резисторе R Ur упадёт до 0, т.к. теперь цепь отключена от вх напр-я (Uвх = 0, Ur+Uc = 0), конд. Начнёт разряжаться и через время t=tu напр-е на нём станет равно 0. Так в цепи с момента t2 изменится направление, а направление на резисторе К в момент t2 скачком будет равно Ur = -Uп и начнёт спадать по
Б) Диф. RL Tu»С Для рассмотрения прохождения импульса следует воспользоваться первым законом коммутации.
В) интегр. RC tu=3C В момент вкл цепи напряжение на входе в силу 2-го закона коммутации = 0, а затем конд будет заряжаться и напряжение на нём будет возрастать по экспоненц. закону.
По истечении времени действия импульса tu конд полностью разряд и в момент времени t2 напр-е на нём достигнет Uп. С этого момента действие импульса на цепь прекратится, конд начинает разряжаться по экси закону и через tп, напр-е на нём спадёт до 0.
Б) диф. RL
XI = W L При вкл. XI очень большая Вых напр-е снимается с катушки индуктивности
Uвых = UI = L
Uвых =
Если посмотреть на схему, то очевидно
Учитывая все уравнения, запишем Uвых =
В) интир. RC Интер.цепь – это четырёх полюсник, у которого Uвых = Kt0 Uвх (t) dt Снимаем напряжение на конденсаторе, составим для данной цепи уравнение, Uвх = RY + Uвых Учитывая что Ic = RC dUc=Uвх-Uвых Разделяя переменные и интегрируя уравнение RC dUc=Uвх-Uвых получаем Uвых = Если Uвых <<Uвх, то получаем Uвых =
Г) интегр RL
Uвых =
4. Применение диф. и инт. цепей. Применение диф. цепей. 1. для выполнения математической операции дифференцирования в сочетании с усилителями в вычислительных машинах непрерывного действия. 2. Для формирования импульсов стороконечной формы из прямоуг. импульсов. 3. Для селекции прямоуг. импульсов по длительности (выд.самые короткие) 4. В кач-ве раздел цепи в усилителях. В этом случае искл. прохождение пост. напр-я коллектора транзистора предыдущего каскада но вход последущего.
Интигр.цепей. 1. для выполнения мат. операций интегр-я. 2. для получения линейного изменения токов и напр-ий. 3. для селекции импульсов по длительности. 4. доля получения целесообразно напр-я из прямоугольных импульсов.
При замыкании ключа ток от источника э.д.с. U потечет по цепи. Очевидно, что согласно второму закону Кирхгофа, должно выполняться Дифференциальное уравнение можно записать в виде:
При установившемся режиме
Очевидно, что постоянной величине приложется U,
Поэтому
Вычитая уравнение 2 из 1, получим
Мы получили дифференциальное уравнение первого порядка с постоянными коэффициентами без правой части. Решаем его, пользуясь преобразованием Лапласа. Очевидно Величина определиться из начальных условий при t=0
Следовательно,
Подставляя его в уравнение получим
Следовательно Оператор Лапласа Ф определиться из PL+R=0. Очевидно, что Обозначив
Постоянная времени Тема №8.
|
||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 262; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.246.44 (0.006 с.) |






 экспоненте Ur = -UuL, а через время t=tu станет равно 0. Т.о., на выходе цепи образуются два острокон. или полож. и отриц. полярностей, площади которых равны, а амплитуда равна Uп.
экспоненте Ur = -UuL, а через время t=tu станет равно 0. Т.о., на выходе цепи образуются два острокон. или полож. и отриц. полярностей, площади которых равны, а амплитуда равна Uп.
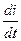


 Ur=Uвх – Uвых
Ur=Uвх – Uвых

 имеем Uвх = RC
имеем Uвх = RC  Uвых = Uвых
Uвых = Uвых
 Uвх (t)dt, где
Uвх (t)dt, где 
 Uвх dt
Uвх dt или, заменяя
или, заменяя  и
и  , получим
, получим  . Учитывая что в момент переходной процедуры
. Учитывая что в момент переходной процедуры  .
. (7.1)
(7.1) следовательно,
следовательно, (7.2)
(7.2)
 ,
, 

 .
.
 .
.

 .
. , получим
, получим  действительный ток в цепи, определяется как сумма токов свободного и принужденного.
действительный ток в цепи, определяется как сумма токов свободного и принужденного.



