Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Однофазные электрические цепи синусоидального тока.Содержание книги
Поиск на нашем сайте
Если в однородном магнитном поле с индукцией В равномерно со скоростью
Если к рамке подключить нагрузку, то в замкнутой цепи пойдет ток, изменяющийся по синусоидальному закону. Значения, при которых ЭДС достигает своих максимальных величин, называются амплитудными, обозначается Промышленный ток изменяется по синусоидальному закону, также как изменяются Э.Д.С. и напряжения: i = Im sin e = Em sin u =Um sin
где i, е, u – мгновенные значения тока, э.д.с. и напряжения соответственно; Im, Em, Um - амплитудные (максимальные) значения тока, э.д.с. и напряжения;
α, α1, α2 – начальные фазы.
Среднее и действующее значение переменного тока.
Среднее значение переменного тока равно величине постоянного тока, при котором через поперечное сечение проводника проходит такое же количество электричества, что и при переменном токе. Обозначается среднее значение тока, напряжения и ЭДС соответственно Определяются средние значения по формулам:
Эффективным или действующим значением переменного тока называется такой ток, который за одинаковый промежуток времени выделит в одном и том же проводнике такое же количество теплоты, что и данный переменный ток. Определяется действующее значение переменного тока, напряжения и ЭДС по формулам:
Векторные диаграммы.
При расчете цепей переменного тока часто приходится суммировать (или вычитать) несколько однородных синусоидально изменяющихся величин одной и той же частоты ƒ, но имеющих разные амплитуды (Im, Em, Um) и начальные фазы (α, α1, α2). Такую задачу можно решать аналитическим путем тригонометрических преобразований или геометрически. Геометрический метод более прост и нагляден, чем аналитический. Синусоидальную величину (например, u = Um sin (wt + α)) изображают в виде радиуса-вектора
α – угол, образованный Пусть необходимо сложить две синусоидальные функции с одинаковым периодом, но разными начальными фазами (см.рис.4): U = Um1 sin (ωt + α1) и U2 = Um2 sin (ωt + α2).
Рис.4 По известному правилу сложения векторов можно получить вектор Вместо того, чтобы вращать векторы с угловой скоростью, можно предположить, что они неподвижны, а оси координат вращаются с угловой скоростью ω. На рис.4 изображено относительное расположение векторов и осей в момент t = 0. Геометрическое построение, описанное выше, определяет амплитуду ОМ =Um, фазу α и тем самым позволяет найти выражение Umsin(ωt + α) = Um1sin(ωt + α1) + Um2sin(ωt + α2), причем амплитуда Um будет равна
фаза α может быть определена через tg α
Аналогично линейная комбинация нескольких синусоидальных функций времени и той же частоты есть синусоидальная функция времени той же частоты:
Часто нужно вычислять производную или интегралы синусоидальных функций времени типа U(t) = Umsin(ωt + α). Имеем
Производные и первообразные от функции U (t) изображаются векторами, повернутыми к исходному вектору соответственно на углы + Изложенное выше применимо в тех случаях, когда требуется произвести сложение, дифференцирование, интегрирование синусоидальных напряжений и токов, либо линейные комбинации этих операций. Но это не применимо, если нужно подвергнуть напряжения или токи нелинейным алгебраическим операциям, как, например, умножению или возведению в степень. При таких операциях возникают круговые частоты, отличные от ω. Это обрекает на неудачу векторное построение, изображенное на рис.4. Построение векторов, изображенное на рис.4, называется векторной диаграммой. Обычно при построении векторных диаграмм вместо амплитудных значений синусоидальных величин берут их действующие значения. Действующие значения переменного напряжения и тока будут равны: Посредством действующих значений напряжения и тока проще выражается активная мощность. Активная мощность является основной величиной, характеризующей энергетические условия в цепи. Если для любого участка цепи известны векторы, длины которых равны действующим значениям напряжения U и тока I, то активная мощность есть скалярное произведение этих векторов:
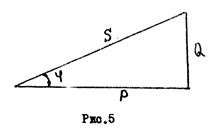
Здесь φ – угол между векторами напряжения и тока. Для электрических расчетов применяют также две вспомогательные величины: полную мощность S = U I, ВА; реактивную мощность Q = U I sin φ, вар. Величины Р, Q, S соотносятся как стороны прямоугольного треугольника. Прямоугольный треугольник, стороны которого численно равны величинам Р, Q, S, называется треугольником мощностей (рис.5).
|
||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 327; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.185.56 (0.007 с.) |

 вращать рамку, то в каждой стороне этой рамки индуктируется ЭДС электромагнитной индукции, которая равна:
вращать рамку, то в каждой стороне этой рамки индуктируется ЭДС электромагнитной индукции, которая равна: (4.1)
(4.1) . При амплитудном значении ЭДС этом
. При амплитудном значении ЭДС этом  и
и  , следовательно
, следовательно  , а
, а  (3.2).
(3.2). t или i = Im sin (
t или i = Im sin ( .
. ……………………………………………………………(4.6),
……………………………………………………………(4.6), ……………………………………………………………(4.7),
……………………………………………………………(4.7), ……………………………………………………………… (4.8).
……………………………………………………………… (4.8). ………………………………………………………………… (4.9)
………………………………………………………………… (4.9) ………………………………………………….(4.10)
………………………………………………….(4.10) ……………………………………………………………….. (4.11)
……………………………………………………………….. (4.11) с декартовыми координатами х=а, у=в (см. рис.3).
с декартовыми координатами х=а, у=в (см. рис.3).

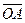 с осью Х в начальный момент времени, называемый начальной фазой. Вектор
с осью Х в начальный момент времени, называемый начальной фазой. Вектор 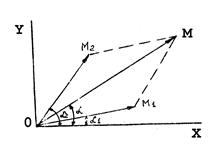
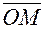 , изображающий сумму обеих функций U1(t) и U2(t), как геометрическую сумму векторов
, изображающий сумму обеих функций U1(t) и U2(t), как геометрическую сумму векторов  , изображающих эти функции. Все три векторы вращаются одновременно с угловой скоростью ω и легко непосредственно проверить, что ордината точки М представляет собой сумму функций Um1sin(ωt + α1) и Um2sin(ωt + α2). Аналогично абсцисса точки М равна сумме функций Um1cos(ωt + α1) и Um2cos(ωt + α2).
, изображающих эти функции. Все три векторы вращаются одновременно с угловой скоростью ω и легко непосредственно проверить, что ордината точки М представляет собой сумму функций Um1sin(ωt + α1) и Um2sin(ωt + α2). Аналогично абсцисса точки М равна сумме функций Um1cos(ωt + α1) и Um2cos(ωt + α2). ,
, .
.

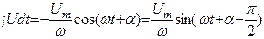 .
. и -
и - 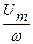 .
. , Вт.
, Вт.