
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 9. Процентные ставки и методы их начисленияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Простые и сложные проценты Предоставляя свои финансовые ресурсы в долг, их собственник рассчитывает получить определенный доход, в виде процентов, начисляемых по некоторому алгоритму в течение определенного промежутка времени. Стандартным временным интервалом в финансовых операциях является один год. Поэтому наиболее распространен вариант, когда процентная ставка устанавливается в виде годовой ставки, подразумевающей однократное начисление процентов по истечении года. Известны две основные схемы дисконтированного начисления процентов: схема простых процентов и схема сложных процентов. Схема простых процентов предполагает неизменность базы, с которой происходит начисление. Пусть PV – исходный инвестируемый капитал, а требуемая доходность – r. Считается, что инвестиция сделана на условиях простого процента, если инвестированный капитал ежегодно увеличивается на величину Pr. Таким образом, размер инвестированного капитала на условиях простого процента (
Схема сложных процентов предполагает, что очередной годовой доход исчисляется не с исходной величины инвестированного капитала, а с общей суммы, включающей также и ранее начисленные, и невостребованные инвестором проценты. В этом случае происходит капитализация процентов, т.е. база с которой происходит начисление постоянно возрастает. Исходя из этого размер инвестированного капитала на условиях сложного процента (
Очень важно помнить, что - при 0 < n < 1 - при n = 1 - при n > 1 Графически взаимосвязь простой и сложной схемы начисления процентов представлена на рис.3.2. Таким образом, в случае ежегодного начисления процентов, для лица, предоставляющего кредит: выгодной является схема простых процентов, если срок ссуды менее одного года (проценты начисляются однократно в конце периода); более выгодной является схема сложных процентов, если срок ссуды превышает один год (проценты начисляются ежегодно); обе схемы дают одинаковые результаты при продолжительности периода в один год и однократном начислении процентов (рис.2).
Рис. 3.2. Простая и сложная схема наращивания капитала Таким образом, в случае ежегодного начисления процентов, для лица, предоставляющего кредит: выгодной является схема простых процентов, если срок ссуды менее одного года (проценты начисляются однократно в конце периода); более выгодной является схема сложных процентов, если срок ссуды превышает один год (проценты начисляются ежегодно); обе схемы дают одинаковые результаты при продолжительности периода в один год и однократном начислении процентов (рис. 3.2). Пример 1. Рассчитать наращенную сумму с исходной суммы 1000 руб. при размещении ее в банке на условиях начисления простых и сложных процентов, если годовая ставка 20 %, период наращивания: 90 дней, 180 дней, 1 год, 5 лет, 10 лет. Решение:
Пример 2. Организация хочет приобрести телекоммуникационное оборудование за 10 млн. руб. Производитель согласен предоставить ссуду на 90 дней, при условии, что организация заплатит за это 14 процентов годовых. Определить выплату? Решение: Поскольку срок инвестирования меньше одного года, воспользуемся формулой простых процентов.
Процедура начисления процентов на проценты (сложные проценты) называются компаундингом. Множитель Пример 3. Вклад 30000 рублей помещен в банк под 5% годовых. Определить сумму на счету через 3 года? Решение: Поскольку срок инвестирования больше одного года, воспользуемся формулой сложных процентов.
В практических расчетах при реализации схемы сложных процентов для быстрой оценки эффективности предлагаемой процентной ставки иногда пользуются приблизительным расчетом времени, необходимого для удвоения инвестированной суммы. Это правило называется «правило 72-х» и заключается в следующем: если r-процентная ставка, выраженная в процентах, то Это правило хорошо срабатывает для небольших значений r (до 20%).
|
||||
|
Последнее изменение этой страницы: 2016-12-29; просмотров: 930; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.153.240 (0.007 с.) |

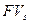 ) будет равен через n лет
) будет равен через n лет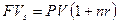 _____________________________________(3.6)
_____________________________________(3.6)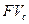 ) к концу n-го года будет равен
) к концу n-го года будет равен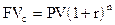 ______________________________________(3.7)
______________________________________(3.7)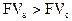
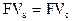
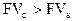
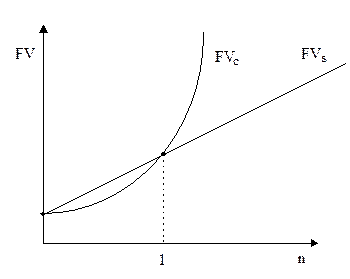
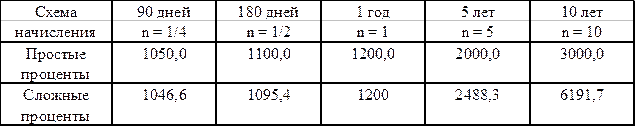
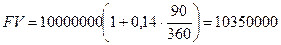 .
.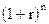 называется коэффициентом аккумулирования.
называется коэффициентом аккумулирования.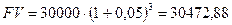
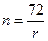 представляет собой число периодов, за которое исходная сумма приблизительно удваивается. Если базовым периодом, т. е. периодом наращивания является год, то в расчете используется годовая ставка, если квартал, то необходимо использовать квартальную ставку.
представляет собой число периодов, за которое исходная сумма приблизительно удваивается. Если базовым периодом, т. е. периодом наращивания является год, то в расчете используется годовая ставка, если квартал, то необходимо использовать квартальную ставку.


