
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Использование фиктивных переменных для моделирования сезонных колебанийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Данный метод заключается в построении модели регрессии, включающей фактор времени и фиктивные переменные. Количество фиктивных переменных определяется как Каждому периоду будет соответствовать свое сочетание фиктивных переменных, каждая из которых равна Например, для временного ряда состоящего из поквартальных данных фиктивные переменные будут следующими, (табл. 66). Общий вид модели регрессии с фиктивными переменными для временного ряда, содержащего циклические колебания периодичностью
Таблица 66
Для ряда состоящего из поквартальных данных:
Уравнение тренда для каждого квартала, таблица 67.
Таблица 67
Величина свободного члена уравнения регрессии
Таблица 68
Параметр Пример 32. Имеются данные об объемах продаж некоего товара поквартально, (табл. 69). Построить модель регрессии с фиктивными переменными. Решение. Для поквартального временного ряда количество фиктивных переменных определяется как:
где Уравнение регрессии примет вид:
В котором одна зависимая переменная
Таблица 69
Проведем регрессионный анализ уравнения. Результаты приведены в таблице 70.
Таблица 70
Уравнение регрессии примет вид:
Проанализируем результаты: 1. критерий Стьюдента показывает, что влияние сезонных компонент статистически значимо 2. Параметр 3. Сезонные колебания в I, II кварталах приводят к снижению 4. Сезонные колебания в III квартале увеличивают параметр 5. Параметр
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-29; просмотров: 650; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.123.118 (0.007 с.) |

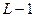 , где
, где  - число периодов в цикле (сезонов внутри года), так при моделировании поквартальных данных модель будет содержать три фиктивные переменные
- число периодов в цикле (сезонов внутри года), так при моделировании поквартальных данных модель будет содержать три фиктивные переменные  и фактор времени
и фактор времени 
 или
или  , сезон, для которого значения всех фиктивных переменных равны
, сезон, для которого значения всех фиктивных переменных равны  (242)
(242) (243)
(243)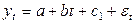



 составит, таблица 68.
составит, таблица 68.


 показывает среднее абсолютное изменение уровней под воздействием тенденции.
показывает среднее абсолютное изменение уровней под воздействием тенденции. ,
,
 , и четыре независимых переменных, из которых
, и четыре независимых переменных, из которых  - фактор времени,
- фактор времени,  - фиктивные переменные. Проставим значение фактора времени и фиктивных переменных в таблицу 69.
- фиктивные переменные. Проставим значение фактора времени и фиктивных переменных в таблицу 69.






 .
. это сумма начального уровня и сезонной компоненты в IV квартале
это сумма начального уровня и сезонной компоненты в IV квартале показывает, что в среднем за квартал объема продаж увеличивается на
показывает, что в среднем за квартал объема продаж увеличивается на 



