
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модели частичной корректировкиСодержание книги
Поиск на нашем сайте
В модели частичной корректировки учитывается не фактическое значение результативного признака
Примером модели частичной корректировки является «модель Литнера», в которой изучается зависимость желаемого объема дивидендов В данной модели предполагается, что фактическое приращение результативного признака
или где
· если · чем ближе · если Подставим
где
Параметры данной модели находим методом обычного МНК, зная данные параметры, через алгебраические преобразования найдем параметры модели Уравнение Уравнение
Пример 45. Имеются данные о объеме дивидендов Построить модель зависимости желаемого объема дивидендов
Таблица 89
Решение. Воспользуемся моделью неполной корректировки
Рассчитаем параметры обычным МНК – таблица 90.
Таблица 90
Значение параметров модели
Из соотношения
Модель зависимости желаемого объема дивидендов
Модели адаптивных ожиданий
В модели адаптивных ожиданий учитывается не фактическое значение факторного признака Например, ожидаемое будущее значение курса рубля Общий вид модели адаптивных ожиданий
где
В данной модели предполагается, что ожидаемое значение фактора
или где
· чем больше · чем меньше · при Подставим в модель
Если модель
Умножим на
Вычтем почленно полученное выражение из
или
где В результате мы получили модель авторегрессии рассчитав параметры которой перейдем к параметрам исходной модели. Для этого при помощи коэффициента при Так как полученная модель включает только фактические значения переменных ее параметры можно определить с помощью стандартных статистических методов. Модель Модель
Контрольные вопросы 1. Какой ряд называется временным (динамическим рядом)? 2. Какие задачи являются основными, при изучении временного ряда? 3. Что называется уровнем динамического ряда? 4. На какие группы можно подразделить все факторы определяющие величину уровня динамического ряда? 5. Приведите аддитивную модель временного ряда? 6. Приведите мультипликативную модель временного ряда? 7. Что такое автокорреляция уровней динамического ряда? 8. Приведите формулу расчета коэффициента автокорреляции. 9. Отчего зависит порядок автокорреляции динамического ряда? 10. Как определить структуру динамического ряда? 11. Приведите основные свойства коэффициента автокорреляции. 12. Что такое тренд динамического ряда? 13. Что такое циклическая компонента временного ряда? 14. Что такое случайная компонента динамического ряда? 15. В чем заключается смысл аналитического выравнивания временного ряда? 16. Какие функции применяют для выравнивания динамического ряда? 17. Как определить вид функции аналитического выравнивания временного ряда? 18. При помощи, каких методов проводят оценку параметров функции выравнивания динамического ряда? 19. Приведите уравнение линейного тренда временного ряда. 20. Приведите систему уравнений для расчета параметров уравнение линейного тренда временного ряда. 21. Приведите уравнение параболы второго порядка временного ряда. 22. Приведите систему уравнений для расчета параметров уравнение параболы второго порядка временного ряда. 23. Расскажите порядок нумерации периодов 24. Расскажите порядок нумерации периодов 25. Что такое случайная компонента динамического ряда? 26. Какие меры колеблемости случайное величины динамического ряда вы знаете? 27. Как рассчитать показатель Ястремского? 28. Что такое экстраполяция? 29. Что такое интерполяция? 30. Как провести экстраполяцию (интерполяцию) графическим методом? 31. Как провести экстраполяцию (интерполяцию) аналитическим методом? 32. Чему должна быть равна сумма сезонных компонент по всем периодам в аддитивной модели? 33. Чему должна быть равна сумма сезонных компонент по всем периодам в мультипликативной модели? 34. Приведите методику использование фиктивных переменных для моделирования сезонных колебаний. 35. Что такое фиктивная переменная в модели регрессии временных рядов? 36. Как определить число фиктивных переменных для модели регрессии временных рядов? 37. Каковы причины возникновения искажений, показателей тесноты и силы связи моделях регрессии временных рядов? 38. Что такое «ложная корреляция»? 39. Приведите основные методы исключения «ложной корреляции». 40. По каким значениям уровней временного ряда проводится корреляционный анализ временных рядов, если используется «метод отклонения от тренда»? 41. Как исключается тенденция во временных рядах, при использовании метода последовательных разностей. 42. Опишите недостатки метода последовательных разностей. 43. В чем заключается метод «включения в модель регрессии фактора времени»? 44. Что такое автокорреляция остатков временных рядов? 45. Опишите основные причины появления остатков во временных рядах? 46. Опишите основные методы определения автокорреляции остатков? 47. Опишите методику использование критерия Дарбина-Уотсона для выявления автокорреляции остатков. 48. Если обнаружена автокорреляция остатков во временных рядах, с помощью какого МНК рассчитываем параметры регрессионной модели? 49. Что такое коинтегрция временных рядов? 50. Как определить наличие коинтеграции во временных рядах? 51. В чем сущность метода использования Критерий Энгеля-Грангера? 52. Как провести тестирование временных рядов на наличие коинтеграции временных рядов при помощи критерия Дарбина-Уотсона 53. Какие временные ряды в эконометрике называют динамическими? 54. Какие динамические модели в эконометрике называют моделями первого типа? 55. Какие динамические модели в эконометрике называют моделями второго типа? 56. Что такое лаговые переменные? 57. Какие переменные содержит динамическая модель с распределенным лагом? 58. Какие переменные содержит динамическая модель авторегрессии? 59. При помощи каких методов проводят оценку параметров динамических эконометрических моделей с распределенным лагом? 60. Как выбрать вид модели с распределенным лагом? 61. Опишите суть метода Алмон. 62. Расскажите о недостатках метода Алмон. 63. Расскажите о преимуществах метода Алмон. 64. Опишите суть метода Койка. 65. Опишите суть метода инструментальных переменных. 66. Опишите методику применения моделей частичной корректировки? 67. Опишите методику применения моделей адаптивных ожиданий? 68.
Вопросы к тестам 1. Временной ряд это: а) произвольно расположенные в произвольном порядке показатели, характеризующие развитие явления во времени; б) последовательно расположенные в хронологическом порядке показатели, характеризующие развитие явления во времени; в) последовательно расположенные по мере возрастания показатели, характеризующие развитие явления во времени.
2. Ряд динамики характеризуется параметрами: а) моментами времени но не содержат уровни ряда; б) уровнями ряда но не отражают момент времени; в) моментами времени и уровнями ряда.
3. Величина уровня временного ряда определяется влиянием: а) трендовой компоненты, сезонной компоненты, случайных факторов; б) трендовой компоненты, случайных факторов; в) трендовой компоненты, сезонной компоненты.
4. Трендовая компонента формирует: а) отражает влияние случайных факторов; б) циклические колебания ряда; в) основную тенденцию ряда.
5. Циклическая компонента формирует: а) отражает влияние случайных факторов; б) сезонное колебание ряда; в) основную тенденцию ряда.
6. Случайная компонента формирует: а) отражает влияние случайных факторов; б) циклические колебания ряда; в) основную тенденцию ряда.
7. Модель временного ряда может быть: а) аддитивной или мультипликативной; б) только мультипликативной; в) только аддитивной.
8. Мультипликативная модель временного ряда это: а) б) в)
9. Аддитивная модель временного ряда это: а) б) в)
10. Автокорреляция уровней динамического ряда это: а) корреляционная связь между произвольно расположенными уровнями одного и то гоже динамического ряда (сдвинутыми на определенный промежуток времени б) корреляционная связь между последовательными уровнями одного и то гоже динамического ряда (сдвинутыми на определенный промежуток времени в) функциональная связь между последовательными уровнями одного и то гоже динамического ряда (сдвинутыми на определенный промежуток времени
11. Коэффициент автокорреляции рассчитывают как: а) б) в)
12. Лаг динамического ряда: а) сдвиг во времени на какое-то количество периодов; б) сума двух уровней временного ряда; в) сума двух и более уровней временного ряда.
13. Порядок коэффициента автокорреляции определяет: а) шаг лага; б) количество уровней динамического ряда; в) моментами и количеством уровней динамики.
14. Последовательность коэффициентов 1-го, 2-го, 3-го и т.д. порядков называется: а) автокорреляционной функцией временного ряда; б) функционал временного ряда; в) средний коэффициент корреляции.
15. Если наибольшим оказался коэффициент автокорреляции 1-го порядка а) то динамический ряд содержит как трендовую компоненту так и циклическую; б) ряд содержит только трендовую компоненту; в) ряд содержит только циклическую компоненту.
16. Если наибольшим оказался коэффициент автокорреляции более высокого прядка а) то динамический ряд содержит как трендовую компоненту так и циклическую; б) ряд содержит только трендовую компоненту; в) ряд содержит только циклическую компоненту.
17. Знак коэффициента автокорреляции: а) указывает на возрастающую или убывающую тенденцию временного ряда; б) не указывает на возрастающую но указывает на убывающую тенденцию временного ряда; в) не указывает на возрастающую или убывающую тенденцию временного ряда.
18. Уровни динамического ряда, при аналитическом выравнивании, выражены как: а) функция времени; б) функция пространства; в) функция времени и пространства.
19. Линейная трендовая модель временного ряда имеет вид: а) б) в)
20. Степенная трендовая модель временного ряда имеет вид: а) б) в)
21. Показательная трендовая модель временного ряда имеет вид: а) б) в)
22. Если в исходном динамическом ряду наблюдаются более или менее постоянные разности первого порядка (абсолютные приросты), то есть не наблюдается тенденция к их увеличению или уменьшению для выравнивания динамического ряда, выбирается: а) парабола второго порядка; б) линейная функция; в) показательная функция.
23. Если в исходном динамическом ряду первые разности сами по себе имеют некоторую тенденцию развития, но вторые разности (абсолютные приросты абсолютных приростов) имеют примерно одну и ту же величину для выравнивания динамического ряда, выбирается: а) парабола второго порядка; б) линейная функция; в) показательная функция.
24. Если рост уровней исходного ряда идет по геометрической прогрессии для выравнивания динамического ряда, выбирается: а) парабола второго порядка; б) линейная функция; в) показательная функция
25. Оценку параметров уравнений а) МДДК; б) МВК; в) МНК.
26. При аналитическом выравнивании по параболе второго порядка а) б) в)
27. При аналитическом выравнивании по прямой а) б) в)
28. Экстраполяция динамического ряда это: а) распространение полученных выводов, полученных в прошлом на будущее время; б) расчет неизвестных промежуточных значений динамического ряда; в) распространение полученных выводов, полученных в будущем на прошлые периоды.
29. В аддитивной модели сумма сезонных компонент по всем периодам должна быть равна: а) числу периодов в цикле; б) нулю; в) от
30. В аддитивной модели случайная компонента равна: а) максимальной ошибке; б) абсолютной ошибке; в) минимальной ошибке.
31. В мультипликативной модели сумма сезонных компонент по всем периодам должна быть равна: а) числу периодов в цикле; б) нулю; в) от
32. Формула корректирующего коэффициента для расчета значений сезонной компоненты в мультипликативной модели: а) б) в)
33. Формула корректирующего коэффициента для расчета значений сезонной компоненты в аддитивной модели: а) б) в)
34. Количество фиктивных переменных для моделирования сезонных колебаний определяется как: а) б) в)
35. Устранение влияния сезонной компоненты, в случае аддитивной модели заключается: а) заключается в умножении ее на исходный уровней ряда как б) заключается в отношении ее из исходных уровней ряда как в) заключается в вычитании ее из исходных уровней ряда как
36. Устранение влияния сезонной компоненты, в случае мультипликативной модели заключается: а) заключается в умножении ее на исходный уровней ряда как б) заключается в отношении ее из исходных уровней ряда как в) заключается в вычитании ее из исходных уровней ряда как
37. «Ложная корреляция» во временных моделях возникает из за: а) наличия трендовой компоненты; б) отсутствия трендовой компоненты; в) во временных рядах «ложная корреляция» отсутствует.
38. При исключении «ложной корреляции» методом отклонения от тренда находят: а) б) в)
39. При исключении «ложной корреляции» методом последовательных разниц, если временной ряд содержит линейный тренд используют: а) разности первого порядка; б) разности второго порядка; в) логарифмические разности.
40. При исключении «ложной корреляции» методом последовательных разниц, если временной ряд содержит тренд в форме параболы второго порядка: а) разности первого порядка; б) разности второго порядка; в) логарифмические разности.
41. Для выявления автокорреляции при помощи критерия Дарбина-Уотсона используется формула: а) б) в)
42. В случае отсутствия автокорреляции критерий Дарбина-Уотсона: а) б) в)
43. В случае наличия положительной автокорреляции критерий Дарбина-Уотсона: а) б) в)
44. В случае наличия отрицательной автокорреляции критерий Дарбина-Уотсона: а) б) в)
45. Если анализ временного ряда выявил наличие автокорреляции в его остатках, то параметры уравнения регрессии находят: а) использую обобщенный метод наименьших квадратов; б) использую классический метод наименьших квадратов; в) метод наименьших квадратов совершенно не приемлем.
46. Коинтеграция временных рядов это: а) причинно-следственная зависимость в уровнях двух и более временных рядов, которая выражается в совпадении или противоположной направленности тенденций данных рядов и случайной колеблемости; б) отсутствие причинно-следственной зависимости в уровнях двух и более временных рядов, которая выражается в совпадении или противоположной направленности тенденций данных рядов и случайной колеблемости; в) наличие регрессионных остатков в пространственных моделях.
47. Между рядами а) фактическое значение б) фактическое значение в) фактическое значение
48. Между рядами а) фактическое значение критерия Дарбина-Уотсона равняется критическому значению; б) фактическое значение критерия Дарбина-Уотсона меньше критического значения; в) фактическое значение критерия Дарбина-Уотсона больше критического значения.
49. Динамической эконометрической моделью временных рядов является модель вида: а) б) в)
50. К динамическим эконометрическим моделям первого типа относят: а) модели неполной корректировки, модели адаптивных ожиданий; б) модели неполной корректировки, модели адаптивных ожиданий, модели с распределенным лагом и модели авторегрессии; в) модели с распределенным лагом и модели авторегрессии.
51. К динамическим эконометрическим моделям второго типа относят: а) модели неполной корректировки, модели адаптивных ожиданий; б) модели неполной корректировки, модели адаптивных ожиданий, модели с распределенным лагом и модели авторегрессии; в) модели с распределенным лагом и модели авторегрессии.
52. Динамическая модель с распределенным лагом, это модель типа: а) б) в)
53. Модель авторегрессии, это модель типа: а) б) в)
54. В динамических моделях с распределенным лагом коэффициент регрессии а) промежуточный мультипликатор; б) краткосрочный мультипликатор; в) долгосрочный мультипликатор.
55. В динамических моделях с распределенным лагом сумма а) промежуточный мультипликатор; б) краткосрочный мультипликатор; в) долгосрочный мультипликатор.
56. В динамических моделях с распределенным лагом сумма всех а) промежуточный мультипликатор; б) краткосрочный мультипликатор; в) долгосрочный мультипликатор.
57. В динамических моделях с распределенным лагом сумма средний лаг рассчитывается как: а) б) в)
58. В динамических моделях с распределенным лагом сумма медианный лаг рассчитывается как: а) б) в)
59. Метод Алмон используется для описания модели: а) в которой величина максимального лага бесконечна и используется допущение о геометрической структуре лага; б) который имеет полиномиальную структуру лага и конечную величину лага; в) который имеет линейную структуру лага. 60. Метод Койка используется для описания модели: а) в которой величина максимального лага бесконечна и используется допущение о геометрической структуре лага; б) который имеет полиномиальную структуру лага и конечную величину лага; в) который имеет линейную структуру лага.
61. Средний лаг для модели Койка рассчитывается как: а) б) в)
62. Медианный лаг для модели Койка рассчитывается как: а) б) в)
63. В динамических моделях авторегрессии коэффициент регрессии а) промежуточный мультипликатор; б) краткосрочный мультипликатор; в) долгосрочный мультипликатор.
64. В динамических моделях авторегрессии произведение а) промежуточный мультипликатор; б) краткосрочный мультипликатор; в) долгосрочный мультипликатор.
65. В динамических моделях авторегрессии показатель а) промежуточный мультипликатор; б) краткосрочный мультипликатор; в) долгосрочный мультипликатор. 66. В моделях частичной корректировки уравнение а) уравнением корреляции МЧК; б) долгосрочной функцией МЧК; в) краткосрочной функцией МЧК.
67. В моделях частичной корректировки уравнение а) уравнением корреляции МЧК; б) долгосрочной функцией МЧК; в) краткосрочной функцией МЧК.
68. Если значение корректирующего коэффициента в МЧК а) не происходит вообще; б) полная корректировка происходит за 1 период; в) модель не имеет смысла.
69. Модель а) краткосрочной функцией модели адаптивных ожиданий; б) долгосрочной функцией модели адаптивных ожиданий; в) среднесрочной функцией модели адаптивных ожиданий.
70. Модель а) краткосрочной функцией модели адаптивных ожиданий; б) долгосрочной функцией модели адаптивных ожиданий; в) среднесрочной функцией модели адаптивных ожиданий.
Ключ к тестовым вопросам
Задачи Задача 21. Имеются данные реализации товаров народного потреб
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-29; просмотров: 652; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.144.98 (0.012 с.) |

 , а его желаемое (ожидаемое) значение
, а его желаемое (ожидаемое) значение  . Общий вид модели частичной корректировки
. Общий вид модели частичной корректировки (274)
(274) .
. пропорционально разнице между ее желаемым уровнем и фактическим значением в предыдущий период
пропорционально разнице между ее желаемым уровнем и фактическим значением в предыдущий период  :
: при
при  (275)
(275) (276)
(276) .
.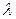 – корректирующий коэффициент.
– корректирующий коэффициент.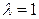 , то
, то  и полная корректировка происходит за 1 период.
и полная корректировка происходит за 1 период. то корректировка не происходит вообще, ожидания не оказывают воздействия.
то корректировка не происходит вообще, ожидания не оказывают воздействия. (277)
(277)






 определим значение корректирующего коэффициента
определим значение корректирующего коэффициента  , соответственно:
, соответственно: ,
, 

 .
. оказывает влияние на инвестиции в отрасль в текущем периоде
оказывает влияние на инвестиции в отрасль в текущем периоде  (278)
(278) при
при  (280)
(280) (устойчивость существующих тенденций).
(устойчивость существующих тенденций).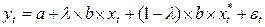 (281)
(281) . В период
. В период 

 (282)
(282) (283)
(283)
 (пример представлен выше).
(пример представлен выше). , при аналитическом выравнивании динамического ряда, если ряд содержит нечетное количество уровней, для достижения условия
, при аналитическом выравнивании динамического ряда, если ряд содержит нечетное количество уровней, для достижения условия  .
. ;
; ;
; .
.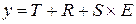 ;
; ;
; .
. - лаг);
- лаг); ;
; ;
; .
.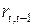 , то:
, то: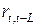 , то:
, то: ;
; ;
; .
. ;
; ;
; .
. ;
; ;
;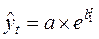 .
. осуществляют при помощи:
осуществляют при помощи: , для оценки параметров уравнения МНК даст систему уравнений:
, для оценки параметров уравнения МНК даст систему уравнений: ;
; ;
; .
. , для оценки параметров уравнения МНК даст систему уравнений:
, для оценки параметров уравнения МНК даст систему уравнений: .
.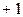 до
до  .
. ;
; ;
; .
. , где
, где 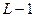 , где
, где  , где
, где  .;
.; ;
; .
.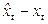 и
и  ;
; и
и  ;
; ;
; ;
; .
. ;
; ;
; .
. меньше критического значения
меньше критического значения  ;
; ;
; ;
; .
. ;
; ;
; .
.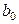 это:
это: это:
это: это:
это: ;
; ;
; .
. ;
; .
. ;
; ;
; .
. ;
; ;
; .
. это:
это: это:
это:


