
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Моделирование сезонных и циклических колебаний временных рядовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В эконометрики для моделирования сезонных и циклических колебаний используют методы: 1. расчет значений сезонной компоненты и построение аддитивной или мультипликативной модели; 2. использование фиктивных переменных и др.
Расчет значений сезонной компоненты и построение аддитивной и мультипликативной модели
Аддитивная модель
используется, если амплитуда сезонных колебаний не меняется со временем. В случае если амплитуда со временем существенно изменяется в ту или иную сторону применяется мультипликативная модель
Построение моделей рассмотрим на примерах.
Пример 30. Имеются данные об объемах продаж некоего товара поквартально, (табл. 62). Необходимо построить модель временного ряда и провести прогнозирование. Решение. 1. Для выбора аддитивной или мультипликативной модели построим график объема продаж – рисунок 15.
Рисунок 15.
По графику видно, что амплитуды колебаний приблизительно равны, поэтому будем строить аддитивную модель Таблица 62
2. Проведем выравнивание фактического временного ряда методом средних скользящих за 4-х летний период (столбец 5).
3. Приведем полученные средние в соответствии с фактическими моментами времени, для чего найдем средние значения из двух последовательных скользящих средних – центрированные скользящие средние (столбец 6).
4. Найдем отклонения
Таблица 63
В моделях с сезонной компонентой все сезонные влияния взаимопоглощаются, т.е. в аддитивной модели сумма сезонных компонент по всем периодам должна быть равна нулю. В нашем случае, это не так -
где, Рассчитаем скорректированную сезонную компоненту:
Сумма всех скорректированных компонент равна нулю. Добавим значения 5. Исключим влияние сезонной компоненты как 6. Используя аналитическое выравнивание ряда
Подставим по порядку в полученное уравнение значение 7. Чтобы найти уровни ряда полученные по аддитивной модели прибавим к значениям ряда
Рисунок 16. Ряд 1 – фактическое потребление, ряд 2 – тренд 8. Случайную компоненту
В аддитивной модели случайная компонента равна абсолютной ошибке. Для оценки качества модели рассчитаем сумму квадратов абсолютных ошибок и сравним с общей сумой квадратов отклонений. В аддитивной модели случайная компонента равна абсолютной ошибке.
Аддитивная модель объясняет 9. Проведем прогнозирование на следующий квартал.
Прогнозное значение объема продаж в следующем, 13-м квартале
Рассчитаем значение трендовой компоненты по полученному уравнению тренда:
13-й квартал является I-м кварталом года, для первых кварталов значение сезонной компоненты Получаем:
Прогноз объема продаж на 13-й квартал составил 893,6 тыс.руб. Пример 31. Имеются данные об объемах продаж некоего товара поквартально, (табл. 64). Необходимо построить модель временного ряда и провести прогнозирование. Решение. 1. Для выбора аддитивной или мультипликативной модели построим график объема продаж – рисунок 17.
Рисунок 17. Таблица 64
По графику видно, что амплитуды колебаний имеют тенденцию к увеличению, поэтому будем строить мультипликативную модель 2. Проведем выравнивание фактического временного ряда методом средних скользящих за 4-х летний период (столбец 5). 3. Приведем полученные средние в соответствии с фактическими моментами времени, для чего найдем средние значения из двух последовательных скользящих средних – центрированные скользящие средние (столбец 6). 4. Найдем отношения
Таблица 65
В мультипликативной модели сумма значений сезонной компоненты по всем кварталам должна быть равна числу периодов в цикле. Для нашей задачи число периодов равно 4-м. у нас же
где, Рассчитаем скорректированную сезонную компоненту:
Сумма всех скорректированных компонент равна 4. Добавим значения 5. Исключим влияние сезонной компоненты как 6. Используя аналитическое выравнивание ряда
Подставим по порядку в полученное уравнение значение 7. Чтобы найти уровни ряда полученные по мультипликативной модели умножим уровни ряда
Рисунок 5. Ряд 18 – фактическое потребление, ряд 2 – тренд 8. Случайную компоненту
Для оценки качества модели рассчитаем сумму квадратов абсолютных ошибок и сравним с общей сумой квадратов отклонений. Абсолютные ошибки в мультипликативной модели рассчитаем как:
Мультипликативная модель объясняет 9. Проведем прогнозирование на следующий квартал. Прогнозное значение объема продаж в следующем, 13-м квартале
Рассчитаем значение трендовой компоненты по полученному уравнению тренда:
13-й квартал является I-м кварталом года, для первых кварталов значение сезонной компоненты Получаем:
Прогноз объема продаж на 13-й квартал составил 1377,83 тыс.руб.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-29; просмотров: 568; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.151.0 (0.009 с.) |

 (230)
(230) (231)
(231)
 .
.

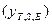













 и т.д.
и т.д.

 и т.д.
и т.д. и используем данные отклонения для расчета значений сезонной компоненты
и используем данные отклонения для расчета значений сезонной компоненты  , (табл. 63).
, (табл. 63).

 , поэтому определим корректирующий коэффициент как:
, поэтому определим корректирующий коэффициент как: (232)
(232) - число сезонов в году.
- число сезонов в году. (233)
(233) , результат занесем в столбец 9 таблицы 62. Полученный временной ряд
, результат занесем в столбец 9 таблицы 62. Полученный временной ряд  содержит только тенденцию и случайную компоненту.
содержит только тенденцию и случайную компоненту.
 столбец 11 таблицы 62.
столбец 11 таблицы 62.

 столбец 12 таблицы 62. (234)
столбец 12 таблицы 62. (234) (235)
(235) общей вариации продаж за последние 12 кварталов.
общей вариации продаж за последние 12 кварталов. это сумма трендовой и сезонной компонент
это сумма трендовой и сезонной компонент (236)
(236)
 (таблица 63).
(таблица 63).

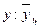





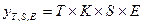 .
. и используем данные отклонения для расчета значений сезонной компоненты
и используем данные отклонения для расчета значений сезонной компоненты  . Поэтому определим корректирующий коэффициент как:
. Поэтому определим корректирующий коэффициент как: (237)
(237) (238)
(238) , результат занесем в столбец 9 таблицы 64. Полученный временной ряд
, результат занесем в столбец 9 таблицы 64. Полученный временной ряд 
 , построим ряд уровней
, построим ряд уровней 

 столбец 12 таблицы 64.
столбец 12 таблицы 64. (239)
(239) (240)
(240) общей вариации продаж за последние 12 кварталов.
общей вариации продаж за последние 12 кварталов.
 (таблица 65).
(таблица 65).



