
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Изучение взаимосвязей временных рядов. Исключение сезонных колебаний и тенденции.Содержание книги
Поиск на нашем сайте
При изучении взаимосвязи временных рядов, методами корреляционно-регрессионного анализа, возникают следующие проблемы: 1. Искажение показателей тесноты и силы связи. Возникает, если один или оба ряда содержат циклические или сезонные колебания. Устранение влияния сезонной компоненты, в случае · аддитивной модели, заключается в вычитании ее из исходных уровней ряда как · мультипликативной модели заключается в отношении ее из исходных уровней ряда как Расчет сезонной компоненты рассмотрен в предыдущей части пособия. 2. Проблема «ложной корреляции». Возникает из за наличия трендовой компоненты. Что избавиться от «ложной корреляции» необходимо исключить тенденцию временного ряда, для чего используют методы: · метод отклонения от тренда; · метод последовательных разностей; · метод включения в модель регрессии фактора времени.
Метод отклонения от тренда При данном методе корреляционный анализ проводится не по фактическим значениям уровней динамического ряда Рассмотрим применение данного метода на примере. Пример 33. Имеются данные за 9 лет о товарообороте магазина N Решение. Проведем проверку рядов на наличие автокорреляции. Коэффициент корреляции
Таблица 71
Устраним тренд методом отклонений от тренда, для чего: 1. Проведем аналитическое выравнивание по прямой каждого ряда, уравнения имеют вид: · · По полученным уравнениям определим расчетные значения 2. Найдем отклонения
Низкие значения коэффициентов автокорреляции свидетельствуют об отсутствии тренда, и полученные ряды отклонений Регрессионная модель имеет вид:
Коэффициент корреляции рядов отклонений Необходимо учитывать, что при построении корреляционно-регрессионной модели по рядам отклонений, полученные параметры не поддаются интерпретации, поэтому данная модель используется только для прогнозирования. Прогнозирование проводится следующим образом: 1. определим трендовое значение факторного признака для интересующего нас периода времени 2. по уравнению тренда для результативного признака определим трендовое значение 3. находим точечный прогноз фактического значения
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-29; просмотров: 829; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |


 .
. и
и  , а по отклонениям фактических уровней от тренда
, а по отклонениям фактических уровней от тренда  и
и  .
. и средней заработной платы жителей ближайшего района
и средней заработной платы жителей ближайшего района 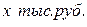 (табл. 71), рассчитать показатели взаимосвязи.
(табл. 71), рассчитать показатели взаимосвязи. . Высокое значение коэффициентов автокорреляции первого порядка
. Высокое значение коэффициентов автокорреляции первого порядка  и
и  , свидетельствует о наличии тренда.
, свидетельствует о наличии тренда.
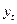
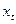






 ,
,  и рассчитаем коэффициент автокорреляции по рядам отклонений.
и рассчитаем коэффициент автокорреляции по рядам отклонений. (знак минус игнорируется, так как по знаку коэффициента автокорреляции нельзя сделать вывод о направлении тенденции)
(знак минус игнорируется, так как по знаку коэффициента автокорреляции нельзя сделать вывод о направлении тенденции)

 .
. , и с помощью одного из методов оценим величину предполагаемого отклонения фактического значения от трендового
, и с помощью одного из методов оценим величину предполагаемого отклонения фактического значения от трендового  .
. , и по уравнению регрессии по отклонениям от трендов найдем величину отклонения
, и по уравнению регрессии по отклонениям от трендов найдем величину отклонения 




