
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Изучение структуры лага, выбор вида модели с распределенным лагомСодержание книги
Поиск на нашем сайте
В модели График зависимости коэффициенты регрессии
Рисунок 22. Линейная структура лага.
Рисунок 23. Геометрическая структура лага.
Рисунок 24. Полиноминальная структура лага (полином второй степени).
Рисунок 25. Полиноминальная структура лага (полином третьей степени). Необходимо учитывать, что получение значения коэффициентов
Метод Алмон Метод Алмон (лаги Алмон) используют для описания модели с распределенным лагом, имеющую полиномиальную структуру лага и конечную величину лага Опишем суть метода Алмон. 1. Модель зависимости коэффициентов от величины лага · 1-й степени · 2-й степени · 3-й степени В общем виде для полинома k-й степени
2. Каждый коэффициент модели · · · · · и т.д. · 3. подставим полученные соотношения
4. перегруппируем слагаемые
5. обозначим слагаемые в скобках при коэффициентах
6. подставим новые переменные в модель, получим
Далее определяем параметры полученной модели обычным МНК. Затем пересчитываем параметры Недостатки метода Алмон: 1. Величина максимального лага 2. Необходимо определить степень полинома 3. Переменные Преимущества метода Алмон: 1. Универсальность. Метод Алмон может быть применен для моделирования процессов которые характеризуются разнообразными структурными лагами. 2. метод Алмон позволяет построить модели с распространенным лагом любой длины при относительно небольшом количестве переменных в модели
Пример 42. Имеются данные о объеме валового выпуска продукции какого то сектора экономики в зависимости от инвестиций в данную отрасль за 25 лет, млрд. руб. (табл. 84). Решение. Построим модель с распределенным лагом при
Проведем преобразование исходных данных в переменные
Результаты преобразований в таблице 84.
Таблица 84
Расчет новой модели вида
Таблица 85
Преобразованная модель имеет вид
Используя найденные коэффициенты регрессии переменных · · · · · и т.д. · найдем коэффициенты регрессии исходной модели.
Модель с распределенным лагом будет иметь вид
Краткосрочный мультипликатор Долгосрочный мультипликатор
Т.е. в долгосрочной перспективе (в нашем примере, через три года) увеличении инвестиций в отрасль приведет к общему росту объема валового выпуска продукции на Относительные коэффициенты регрессии рассчитаем как
Видно, что воздействие фактора на результат проявляется со второго года. Средний лаг будет равен
То есть, в среднем увеличении инвестиций в отрасль приведет к росту объема валового выпуска продукции через 1,95 года.
Метод Койка
Если имеется динамическая модель с распределенным лагом в которой величина максимального лага бесконечна,
то применение обычного МНК или других стандартных методов определения параметра модели невозможно. При этом используют допущение о геометрической структуре лага – воздействие лаговых значений фактора на результативный признак уменьшается с увеличением лага фактора в геометрической прогрессии. Именно для таких моделей Л.М. Койк сделал предположение позволяющее рассчитывать их параметры, которое получило название «метод Койка» или «Модель Койка». Суть данного предположения заключается в том, что существует постоянный темп · ограничение · ограничение Модель Койка имеет вид
где Модель Койка это двухфакторная модель авторегрессии. Рассчитав ее параметры, мы найдем Далее используя соотношения Средний лаг для модели Койка рассчитывается как
Медианный лаг равен
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-29; просмотров: 696; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.200.197 (0.008 с.) |

 коэффициенты регрессии
коэффициенты регрессии  при факторных переменных показывают количественно силу связи между результатом и соответствующим фактором
при факторных переменных показывают количественно силу связи между результатом и соответствующим фактором  .
.



 .
. формально представляет собой полином:
формально представляет собой полином:


 (256)
(256)
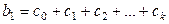


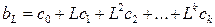 (257)
(257) (258)
(258) (259)
(259) как новые переменные
как новые переменные (260)
(260) (261)
(261) и лаговыми значениями фактора
и лаговыми значениями фактора  . Если теснота связи значима, то лаговое значение фактора включается в модель.
. Если теснота связи значима, то лаговое значение фактора включается в модель. (как правило,
(как правило,  или
или  ). Выбранная степень должна быть на единицу меньше экстремумов в структуре лага. Величину
). Выбранная степень должна быть на единицу меньше экстремумов в структуре лага. Величину  , которые определенны как линейные комбинации факторов
, которые определенны как линейные комбинации факторов  , будут коррелировать между собой, если между факторными признаками существует тесная связь. Поэтому для модели вида
, будут коррелировать между собой, если между факторными признаками существует тесная связь. Поэтому для модели вида  и предположении, что структура лага описывается полиномом второй степени. Исходная модель будет иметь вид
и предположении, что структура лага описывается полиномом второй степени. Исходная модель будет иметь вид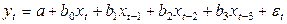
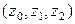








 проведем обычным МНК, результаты в таблице 85.
проведем обычным МНК, результаты в таблице 85.






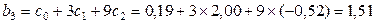
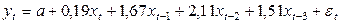
 , показывает, что при увеличении инвестиций в отрасль на
, показывает, что при увеличении инвестиций в отрасль на  объем валового выпуска продукции в среднем увеличится на
объем валового выпуска продукции в среднем увеличится на  в том же периоде.
в том же периоде.







 (262)
(262)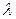 , при
, при  .
. дает одинаковые значения всех коэффициентов
дает одинаковые значения всех коэффициентов 
 показывает, что с увеличением лага значения параметров модели
показывает, что с увеличением лага значения параметров модели  (263)
(263)
 исходной модели (необходимо помнить, что применение обычного МНК для моделей авторегрессии дает смещенные оценки, примеры расчета представлены далее).
исходной модели (необходимо помнить, что применение обычного МНК для моделей авторегрессии дает смещенные оценки, примеры расчета представлены далее). определим параметры
определим параметры  модели
модели  (264)
(264) (265)
(265)


