
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Коинтеграция временных рядовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Наличие тенденции в одном из временных рядов не всегда есть результат воздействия случайных причин, тенденция одного из рядов может быть результатом того, что другой временной ряд, включенный в модель также содержит тенденцию, вследствие чего коэффициент корреляции, рассчитанный по уровням таких рядов (содержащих одинаково или противоположно направленную тенденцию) может не содержать ложную корреляцию, а характеризовать истинную взаимосвязь. Коинтеграция временных рядов – причинно-следственная зависимость в уровнях двух и более временных рядов, которая выражается в совпадении или противоположной направленности тенденций данных рядов и случайной колеблемости. Наличие коинтеграции временных рядов определяю при помощи специальных критериев, наиболее часто используют: · Критерий Энгеля-Грангера · Критерий Дарбина-Уотсона.
4.2.6.1. Критерий Энгеля-Грангера определения коинтеграции временных рядов Рассмотрим анализ модели Сущность данного метода заключается в расчете фактического значения
где
где;
Далее фактическое значение
Таблица 79. Критические значения
Если фактическое значение
Пример 39. Имеются данные о среднемесячной прибыли Необходимо проверить модель
Таблица 80
Решение. 1. Рассчитаем значения 2. Найдем 3. Построим где
Получили
4. Фактическое значение
4.2.6.2 Критерий Дарбина-Уотсона определения коинтеграции временных рядов Тестирование рядов на наличие коинтеграцции временных рядов При этом фактическое значение критерия Дарбина-Уотсона, рассчитанное как:
сравнивают с критическим значением для разных уровней значимости (табл. 81).
Таблица 81. Критические значения критерия Дарбина-Уотсона, полученные методом Монте-Карло.
Если фактическое значение критерия Дарбина-Уотсона больше критического значения, то говорят о наличии коинтеграции между рядами
Пример 40. Имеются данные о среднемесячной прибыли
Таблица 82
Необходимо проверить модель Решение. 1. Рассчитаем фактическое значение критерия как:
2. Для нашего примера, при
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-29; просмотров: 1110; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.31.82 (0.006 с.) |

 на наличие коинтеграции временных рядов, используя критерий Энгеля-Грангера.
на наличие коинтеграции временных рядов, используя критерий Энгеля-Грангера. для коэффициента
для коэффициента  в уравнении
в уравнении (248)
(248)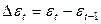 - первые разности остатков (абсолютные приросты), из соотношения
- первые разности остатков (абсолютные приросты), из соотношения 

 - коэффициент регрессии.
- коэффициент регрессии. - стандартная ошибка коэффициента регрессии
- стандартная ошибка коэффициента регрессии , рассчитанным Энгелем и Грангером для разных уровней значимости (табл. 79).
, рассчитанным Энгелем и Грангером для разных уровней значимости (табл. 79).
 и
и  .
.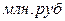 и затратах на рекламу
и затратах на рекламу  (табл. 80).
(табл. 80). , используя критерий Энгеля-Грангера.
, используя критерий Энгеля-Грангера.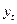
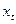


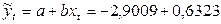 (табл. 80)
(табл. 80)

 , больше критического значения
, больше критического значения 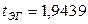 . Соответственно с вероятностью 95% можно сделать вывод о наличии коинтеграции временных рядов.
. Соответственно с вероятностью 95% можно сделать вывод о наличии коинтеграции временных рядов. о том, что фактическое значение критерия Дарбина-Уотсона в генеральной совокупности равно нулю.
о том, что фактическое значение критерия Дарбина-Уотсона в генеральной совокупности равно нулю. (249)
(249)




