
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод последовательных разностейСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Тенденцию во временных рядах можно устранить, заменив фактические ряды на ряды последовательных разностей разных порядков, в зависимости от формы тренда. Если временной ряд содержит: · линейный тренд, то используют разности первого порядка (абсолютные приросты). Рассмотрим линейная модель имеет вид тогда разности первого порядка
где Если ряд содержит сильную линейную тенденцию, то остатки · тренд в форме параболы второго порядка, используют разности второго порядка. Рассмотрим модель параболы второго порядка имеет вид тогда разности второго порядка
Вторые разности не содержат тенденцию. · экспоненциальный или степенной тренд, метод последовательных разностей следует применять не к исходным уровням ряда, а к их логарифмам. Метод последовательных разностей имеет следующие недостатки: 1. имеет место сокращение числа пар наблюдений, по которым строится уравнение регрессии, соответственно понижается число степеней свободы 2. использование не фактических уровней, а их приростов ведет к потере информации исходных данных
Пример 34. Имеются данные за 9 лет о товарообороте магазина N
Таблица 72
Решение. Исключим тренд методом последовательных разностей. Найдем первые разницы (абсолютные приросты) исходных рядов Расчетные ряды Коэффициент корреляции рядов Регрессионная модель имеет вид:
Параметры уравнения построенного по методу последовательных разностей поддаются интерпретации. При увеличении средней заработной платы на
Включение в модель регрессии фактора времени Данный метод предполагает включение в модель регрессии
Данный метод имеет наиболее широкое применение по сравнению с методом последовательных разностей и методом отклонения от тренда, так как позволяет учесть всю информацию данных, и интерпретация полученных параметров не вызывает затруднений. Пример 35. Имеются данные за 9 лет о товарообороте магазина N
Таблица 73
Решение. Исключим тренд методом включение в модель регрессии фактора времени. Добавим в модель переменную времени
Параметр
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-29; просмотров: 1072; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.109.251 (0.028 с.) |




 - константа, не зависящая от времени.
- константа, не зависящая от времени. будут достаточно малы и носят случайный характер, следовательно, первые разности уровней временных рядов не содержат временную тенденцию.
будут достаточно малы и носят случайный характер, следовательно, первые разности уровней временных рядов не содержат временную тенденцию.

 и средней заработной платы жителей ближайшего района
и средней заработной платы жителей ближайшего района 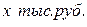 (табл. 72).
(табл. 72).
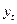
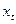


 и
и 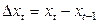
 и
и  -
-  .
.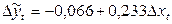
 товарооборот магазина увеличится в среднем на
товарооборот магазина увеличится в среднем на 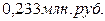
 переменную времени
переменную времени  (244)
(244) и средней заработной платы жителей ближайшего района
и средней заработной платы жителей ближайшего района  (табл. 73)
(табл. 73)

 показывает, что при увеличении средней заработной платы
показывает, что при увеличении средней заработной платы  , параметр
, параметр  показывает влияния всех остальных факторов.
показывает влияния всех остальных факторов.


