Возникновение и История логики

Логика представляет собой одну из самых древних наук. Она возникла около двух с половиной тысяч лет назад одновременно на территории двух государств Древнего мира: Древней Греции и Древней Индии.

Основателем древнегреческой традиции логики является Аристотель (384-322 гг. до н.э.). Аристотель написал несколько сочинений по логике, среди которых «Первая и Вторая Аналитики», «Топика», «Категории» и т.д.

Впоследствии логические труды Аристотеля получили общее название «Органон» (т.е. «орудие познания»).

Это интересно: Аристотель родился в семье придворного врача македонского царя, впоследствии он выучился и стал личным наставником Александра Македонского, оказав на него колоссальное влияние. Основная учеба Аристотеля прошла в академии Платона, но спустя некоторое время Аристотель покинул его школу, заявив: «Платон мне друг, но истина дороже», и основал свою школу, назвав ее Ликей (т.е. наш будущий «лицей»). Аристотелю принадлежит множество мудрых высказываний. К примеру, когда его упрекали, что он подавал милостыню человеку дурного нрава; он ответил: «Я подаю не нраву, а человеку». Когда ему сказали, что кто-то бранит его заочно, он сказал: «Заочно пусть он хоть бьет меня». Один болтун, сильно докучавший ему своим пустословием, спросил его: «Я тебя не утомил»? Аристотель ответил: «Нет, ведь я не слушал».

Аристотель очень ценил развитие ума, считал это фактически главной задачей логики. Его труды были продолжены многими мыслителями западного мира: Боэцием (V-VI вв.), Иоанном Дамаскином (VII-VIII вв.), Фомой Аквинским (1225-1274), Декартом (1596-1650), Бэконом (1561-1626), Лейбницем (1646-1716), Кантом (1724-1804), Гегелем (1770-1831), Миллем (1806-1873) и многими другими. В двадцатом веке наиболее известны логические достижения Фреге (1848-1925) и Витгенштейна (1889-1951).

Основателем древнеиндийской традиции логики считается Гаутама (не стоит путать с Буддой, родовое имя которого также было Гаутама). Гаутама систематизировал разрозненные логические представления своих предшественников и написал труд «Ньяя-сутры», где ньяя – синоним логики, сутра – жанр философского произведения.

Это интересно: Существует целый ряд легенд, связанных с Гаутамой. В одной из них повествуется, что однажды к нему в школу логики поросился учиться безвестный мальчик. По индийской традиции Гаутама спросил мальчика о том, кто его отец. Однако тот не знал этого и пошел к матери, чтобы узнать. Мать ответила, что она – проститутка, и его отец, скорее всего, низкий человек, посчитавший возможным за деньги воспользоваться женским телом. Узнав обстоятельства своего рождения, мальчик пришел к Гаутаме и решительно сказал, что не сможет учиться в его школе, так как его происхождение крайне сомнительное. Однако Гаутама с радостью принял его в школу, провозгласив, что его честность, а не происхождение – лучший критерий его готовности учиться.

В действительности основным занятием Гаутамы была йога, важнейшей целью которой является контроль деятельности ума, ведь именно от необузданного ума, его чрезмерных желаний и эмоций, происходит большее количество человеческих проблем. Поэтому в отличие от Аристотеля главной задачей логики Гаутама считал отнюдь не развитие мышления, а его контроль. Таким образом, наука логики в его случае носила обслуживающий характер, она исследовала ум для нужд йоги.

Труды Гаутамы были в дальнейшем продолжены такими его последователями как Ватсьяяна (IV-V вв.), Удаяна (X-XI), Гангеша (XII в.), Чайтанья (1486-1534), Рагхунатха (1477-1547). Большой вклад в развитие индийской логики внесли и буддийские мыслители: Дигнага (V-VI вв.), Дхармакирти (VII в.), Дхармоттара (VIII в.) и др.

Первым, кто стал систематически заниматься логикой в России, был М.В. Ломоносов (1711-1765). Логика глубоко интересовала А.Н. Радищева (1749-1802) и Н.Г. Чернышевского (1828-1889). В двадцатом веке отечественная школа логики дала миру таких известных ученых как Г.И. Челпанов (1862-1936), Е.К. Войшвилло (1913-2008), Э.В. Ильенков (1924-1979). Русская и советская логика не только удачно впитала в себя все основные достижения мировой логики, но и предложила целый ряд значительных открытий.

 

Основные логические законы

 

В логике существует своеобразная «конституция» мышления, состоящая из четырех главных законов человеческого ума. Первые три закона были открыты очень давно, еще Аристотелем, поместившим их в своем знаменитом труде «Метафизика». В Индии подобные законы (второй и третий законы воспринимались как единое целое) упомянуты в сочинениях Дигнаги и Гангеши. Наконец, четвертый закон стал известен сравнительно недавно, заслуга его открытия принадлежит Лейбницу.

Закон тождества: Любая мысль, используемая в рассуждении, должна выражать только саму себя, а не какую-то другую мысль.

Как правило, данный закон нарушается при неверном использовании омонимов и подобных им выражений. Омонимы – слова, которые одинаково звучат или пишутся, но имеют разные смыслы: «лук», «коса», «шах», «мир» и др. Использование синонимов, напротив, не только допускается, но часто обогащает речь. Здесь можно вспомнить знаменитый исторический казус, связанный с приказом царя Ивана Грозного: «Казнить нельзя помиловать»! Без правильной постановки запятой мысль делает смысловую «вилку», и ее становится возможным понять и в смысле указания на помилование, и в смысле приказа о казни.

Это интересно: Авторы анекдотов прекрасно знают, что в большинстве анекдотов сознательно нарушен закон тождества, в силу чего и возникает анекдотическая ситуация, вызывающая смех. Приведем пример:

Звонок по телефону:

– Алло! Это пожарная?

– Да, пожарная.

– Пожарьте, пожалуйста, картошки!

– Нет-нет, мы не жарим, мы тушим!

– О! Еще лучше – потушите!

Очевидно, что слова-омонимы «жарить» и «тушить» оказались причиной сложившегося недоразумения.

 

Закон непротиворечия: Две противоречащих друг другу мысли не могут быть одновременно истинными, одна из них обязательно должна быть ложной.

К примеру, если мы точно знаем, что студент Петров присутствует на лекции, то никак не может быть одновременно верным, что он не присутствует. Третий закон очень похож на предыдущий и поэтому в Индии он не выделялся в качестве отдельного правила мысли. Этот закон третий по счету и говорит о «третьем», поэтому его легко запомнить.

Закон исключенного третьего: Две противоречащих друг другу мысли не могут быть одновременно ложными, одна из них обязательно должна быть истинной.

Пример тот же. Если некто утверждает, что студент Петров не присутствует на лекции, но мы точно знаем, что это ложь, то Петрову некуда будет деться, кроме, как только присутствовать на лекции, а, значит, последняя мысль будет истиной.

Из второго и третьего закона выделяют ряд исключений. Обозначим главные из них:

- Исключение первое: Второй и третий законы не вступают в силу, когда говорится о разных предметах, т.е. используются уже известные нам омонимы. Скажем, под Петровым мы на самом деле имеем двух однофамильцев – Ивана Петрова и Евгения Петрова. Тогда вполне может быть, что одновременно один из них присутствует, а другой отсутствует.

- Исключение второе: Второй и третий законы не вступают в силу, когда говорится об одном и том же предмете, но в разное время. Скажем, один и тот же Петров может присутствовать на лекции в 12-00, но отсутствовать в 16-00.

- Исключение третье: Второй и третий законы не вступают в силу, когда говорится об одном и том же предмете, но в разных отношениях. Скажем, один и тот же Петров может присутствовать на лекции по логике, но одновременно с этим отсутствовать на лекции по математике.

Это интересно: Когда первооткрыватель закона непротиворечия в Индии – Дигнага завершил свой труд по логике, на стене своей пещеры для медитации он написал эпиграф, прославляющий логику, а затем ушел собирать подаяние. Но когда он вернулся, то увидел, что написанное им затерто. На следующий день он вновь написал его, но затем оно снова оказалось стертым. Так продолжалось несколько дней, и поэтому Дигнага написал на стене: «Если Вы стираете, просто чтобы пошутить – пожалуйста, не делайте этого! Логика – не шутки! Если Вы завидуете красоте стиха, то стирать бесполезно – я хорошо помню этот стих. Если же Вы не согласны, то приходите спорить»! На следующий день у входа в пещеру его ждал другой ученый, с которым они непрерывно дискутировали в течение нескольких дней, но никто не мог окончательно победить. Тогда Дигнага провозгласил: «Сейчас я подброшу вверх перо, которым написал этот труд по логике, и когда оно коснется земли, я откажусь от своих логических исследований»! Но когда он подбросил перо, сильный порыв ветра унес его далеко в небо, и его оппонент признал себя проигравшим.

 

Закон достаточного основания: Любая мысль для того, чтобы быть верно использованной должна иметь достаточное основание, т.е. быть доказанной.

Перед открытием последнего закона логики на Западе прошло фактически два тысячелетия. Следует отметить, что в Индии данный закон не был зафиксирован как таковой в силу его очевидности. Действительно, любой нормальный человек требует доказательств тому, в чем он не уверен. Никто из нас не пойдет за медицинской помощью к неспециалисту, и не будет жить в доме, построенном вне правил архитектуры.

 

Структура познания

 

Человеческое познание имеет сложную пористую структуру, философы изучают его уже более двух тысячелетий, и даже сейчас мы можем сказать, что человечество в данном отношении знает не так уж много. Многие аспекты познания до сих пор являются объектами неутихающих споров. Однако некоторые принципиальные вещи мы о познании сказать все-таки можем. Так, большинство мыслителей сходятся в том, что наше познание, по большому счету, имеет трехуровневую структуру:

Уровень первый: Чувственное познание, т.е. познание, осуществляемое за счет пяти известных нам чувств: слух, осязание, зрение, вкус, обоняние. Оно, в свою очередь, подразделяется на три подуровня, или формы.

Ощущение – фиксация в сознании человека отдельных свойств (звук, температура, цвет, вкус, запах) какого-либо предмета. При ощущении мы фактически знаем, что перед нами что-то есть, но еще не знаем, что. Скажем, мы смотрим вдаль и видим то ли столб, то ли человека. Это ощущение.

Восприятие – фиксация в сознании человека целостного образа предмета. В нашем примере, мы подходим ближе и видим, что это все-таки столб. Это восприятие.

Представление – фиксация в сознании человека образа предмета, воспринимавшегося ранее. Представления хранятся в памяти. Стоит нам вспомнить кого-то, кто сейчас не находится рядом с нами. Это будет представление.

Однако мы можем констатировать как факт, что чувства не предоставляют нам полной и всегда правильной информации об окружающем мире. Мы слышим, видим и т.д. в определенном диапазоне. Также чувства зачастую искажают информацию. Так, мы видим, как ложка преломляется в стакане с чаем, регистрируем наличие горизонта, хотя нигде земля не сходится с небом, и т.д.

Уровень второй: Рациональное познание или мышление (ratio – «разум», латынь). Оно также включает в себя три подуровня, или формы. На данном этапе мы дадим им лишь предварительные определения.

- Понятие – любое слово или словосочетание, смысл которого нам понятен. Для наглядности мы можем вывести простую формулу:

 

ПОНЯТИЕ = СЛОВО + его СМЫСЛ

Очевидно, что часть слов остаются для нас не понят ными, другими словами, мы не знаем их смысл. Однако любое слово или словосочетание, смысл которого нам понят ен, является уже понятием. Примеры понятий: «стул», «стол», «зеленое дерево», «красивая девушка», «Алтайский государственный аграрный университет» и т.п.

Суждение – любое предложение или фраза, над смыслом которого мы можем рас суждать. Любое суждение состоит из понятий. Формула:

 

СУЖДЕНИЕ = ПРЕДЛОЖЕНИЕ + его СМЫСЛ

 

Примеры суждений: «Красивая девушка села на стул», «Около АГАУ стоит памятник М. А. Лисавенко». Конечно, бессмысленные предложения не будут являться суждениями. Пример: «Треугольники округло квадратничали». Очевидно, это предложение, но, скорее, не суждение.

Умозаключение – любой осмысленный вывод, посредством которого мы заключаем что-либо в нашем уме. Каждое умозаключение состоит из суждений. Формула:

 

УМОЗАКЛЮЧЕНИЕ = СУЖДЕНИЕ 1 + СУЖДЕНИЕ n

(где n –количество)

 

Примеры умозаключений: «Все студенты должны сдавать экзамены, Петров является студентом, следовательно, Петров должен сдавать экзамены»; «Девушки нашей группы сдали экзамен, парни нашей группы сдали экзамен, следовательно, вся наша группа сдала экзамен». Отметим, что темы «Понятие»; «Суждение»; «Умозаключение» фактически составляют весь нижеследующий курс логики.

Однако сила нашего ума тоже не беспредельна, его способности реально ограничены. Попытайтесь, не сходя с места и не пользуясь никакими средствами, перемножить в уме 345876 на 890321. Сделать это будет достаточно сложно. А порой ум совершает ошибки – кто их не делал на уроках математики или у магазинной кассы?

Это интересно: В индийской логике существует забавная басня. Жил-был в одном озере старый крокодил. И однажды на берег этого озера пришла женщина с маленьким ребенком. Женщина стала стирать одежду, а малыш принялся строить песочные замки. Вдруг мать ребенка слышит крик и видит, что ее малыша схватил крокодил. Упав на колени, она просит, чтобы он отпустил его. Тогда крокодил говорит ей:

- Я согласен, я отпущу его, но ты должна отгадать одну загадку.

Женщина:

- Все, что угодно!

Крокодил:

- Отгадай, что я сейчас буду делать?

Умная женщина взяла паузу и спустя некоторое время ответила:

- Ты не отдашь моего ребенка...

Крокодил начинает думать: «Итак, если я не отдам ей ребенка, то она – угадала, и я должен его отпустить. Нет! Так не пойдет! Но если я отдам ей ребенка (что само по себе не радует), то она не угадала, и я не должен его отпускать...». Крокодил думал так и сяк, но ни один из вариантов не удовлетворял его. В конце концов, он умер от перенапряжения, а женщина освободила сына. В данной басне крокодил символизирует наш ум, который порой «виснет» подобно компьютеру, который не может выбрать из нескольких вариантов один необходимый.

 

В случаях, когда человеку не могут помочь ни чувства, ни мышление, он часто обращается к интуиции.

Уровень третий: Интуитивное познание. Оно, в свою очередь, подразделяется на два подуровня.

Религиозная интуиция – фиксирующая в сознании человека его отношение к проблемам веры или ее отсутствие. Заметим, что атеистически настроенный человек здесь не менее верит, чем верующий.

Бытовая интуиция – фиксирующая в сознании человека его отношение к вопросам межличностных отношений, общения, творчества и т.п. Такие наиважнейшие аспекты нашей жизни как «дружба», любовь», «речь», «творчество» (музыка, стихи, изобразительное искусство и др.) имеют самое прямое, хотя и не исключительное, отношение к интуитивному познанию. Однако стоит ли говорить, что действие интуиции зачастую кратковременно, и она порой подводит человека.

Таким образом, мы можем заключить, что все три уровня познания должны содействовать друг другу. Мышление, являющееся объектом логики, располагается между чувствами и интуицией. Мышление фактически целиком опирается на данные чувств, а в ситуациях, когда мышление не может справиться с поставленной задачей, оно уступает место интуиции.

 

Контрольные вопросы:

1. Как Вы определите объект и предмет науки логики?

2. Какие мыслители являются основателями греческой и индийской логических традиций?

3. Сколько главных законов логики Вы знаете, каковы их формулировки?

4. Каково место мышления в структуре человеческого познания?

Вопросы к зачету по данному разделу:

· Предмет логики. Отличие от других наук о мышлении.

· История логики.

· Четыре основных логических закона.

· Структура познания.

Понятие как форма мышления

Определение понятия. Существенные и несущественные признаки понятий. Содержание и объем понятия. Закон обратного отношения между объемом и содержанием понятия. Классификация понятий. Отношения между понятиями. Основные операции с понятиями: определение, виды и правила определений; деление, виды и правила делений.

 

Определение понятия

В каком-то смысле мы живем в мире понятий, так как подавляющее большинство предметов, которые окружают нас, обладают для нас определенным смыслом. Тем более важно разобраться в том, что такое понятие. Ранее мы давали предварительное определение понятия, теперь же пришло время дать ему строгое логическое определение.

Понятие – это форма мышления, выражающая предметы через их существенные признаки. Слово «форма» подразумевает, что наша мысль, как и многое другое, может быть облечена в определенные конструкции – подобно тому, как мы можем «втискивать» в конкретные формы песок, тесто и даже наше тело.

Из определения становится ясно, что каждый предмет обладает набором признаков, главные из которых следующие.

Существенные признаки – признаки, выражающие суть предмета, при их отсутствии предмет не может оставаться самим собой, он теряет свой смысл. Такие признаки обязательны. Например, существенным признаком человека является то, что он – существо, обладающее сознанием, разумом; существенным признаком яблока является то, что оно – фрукт и т.д. Чтобы найти существенные признаки предмета достаточно попытаться ответить на следующие вопросы: В какую общую группу предметов входит данное понятие? Какова основная функция предмета? Каково его происхождение? Какова принципиальная структура предмета?

Несущественные признаки – признаки, являющиеся косвенными для предмета, они могут как присутствовать, так и отсутствовать. Такие признаки необязательны. Например, рост 170 см. не является существенным для человека, так как человек может быть и другого роста; яблоко не обязательно может быть красным и т.п. Нетрудно заметить, что именно существенные признаки образуют, «сгущают» смысл предмета, поэтому как раз они подразумеваются в любом понятии. Это очень легко проверить. Ведь если мы попросим Вас объяснить незнакомому человеку, что такое «корова», все будут, в первую очередь, называть существенные признаки: млекопитающее, крупное домашнее животное, ее разводят для получения мяса и молока. Но отнюдь не будут перечислять несущественные признаки, скажем: бывает весом 350 кг, коричневая, алтайская и т.д.

 

Содержание и объем понятия

 

Каждое понятие, как, впрочем, и любой предмет вообще обладает двумя важными характеристиками: содержанием и объемом. Однако необходимо различать логические объем и содержание, и подобные же физические параметры. Логические содержание и объем имеют дело со смыслом предмета, физические – с его физическими характеристиками.

Содержание – совокупность существенных признаков предмета. Чтобы выявить примерное содержание понятия, стоит попытаться ответить на вышеперечисленные вопросы, касающиеся существенных признаков предмета. Например, в содержание понятия «автомобиль» входят следующие признаки: транспорт, имеет вес, сконструирован человеком, имеет мотор и т.д.

Объем – совокупность предметов, которые могут быть обозначены данным понятием. Любая разновидность предмета входит в его объем. Скажем, объем понятия «автомобиль» включает следующие предметы: грузовик, Мерседес, отечественный автомобиль, дорогой автомобиль и т.п.

В отношении объема понятия можно совершать две логических операции:

Ограничение – логическая операция по уменьшению объема понятия. Другими словами, мы ищем понятие, которое является разновидностью исходного понятия. Скажем, ограничивая объем понятия «мебель», мы можем получить «стул», «стол», «кресло» и т.д. Ограничивая объем понятия «стол», мы можем прийти к понятию «кухонный стол», «письменный стол» и т.п.

Обобщение – логическая операция по увеличению объема понятия. Иначе говоря, мы ищем понятие, для которого, напротив, исходное понятие представляет собой разновидность. Так, обобщая понятие «яблоко», мы получим «фрукт». Обобщая далее, получим «плод», затем «продукт питания», и т.д., продолжая цепочку.

В логике давно замечено, что отношения между объемом и содержанием понятия могут быть выстроены по принципу «сообщающихся сосудов» или принципу обратной пропорциональности.

 

Закон обратного отношения между объемом и содержанием понятия: При увеличении объема понятия, его содержание уменьшается; а при уменьшении объема понятия, его содержание увеличивается, и наоборот.

К примеру, если мы возьмем понятие «Земля»» и обобщим его до понятия «планета», то естественно объем «планеты» будет включать в себя гораздо большее количество предметов, нежели понятие «Земля». Однако вместе с тем, будет необходимым отметить, что понятие «планета», напротив, гораздо беднее по содержанию, чем «Земля». Так мы не можем сказать, что такие существенные признаки Земли, как «населенная», «имеет спутник», «вертится вокруг Солнца» будут таковыми и для понятия «планета». Напомним, что согласно определению, именно существенные признаки составляют содержание любого понятия.

 

Классификация понятий

Способность классифицировать что-либо, «раскладывать по полочкам» – одна из основных логических операций, к которым склонен человек. Не составляют исключения и понятия. Существенный вклад в решение проблемы классификации понятий внес великий немецкий философ Иммануил Кант.

 

Это интересно: Иммануил Кант был человеком очень строгих принципов. Он не стал жениться, так как справедливо полагал, что супруга и дети будут отвлекать его от занятий науками. Кант всю жизнь прожил в Кеннингсберге (в настоящее время - Калининград) и занимал должность ректора в местном университете. Вся жизнь Канта была строго упорядочена: он в определенное время вставал, кушал, работал, встречался с людьми и занимался творчеством. Только однажды он нарушил свой распорядок – зачитался книгой французского мыслителя Мишеля Монтеня «Опыты». Известно, что императрица Елизавета приглашала Канта работать в Москву, но тот отказался. Могила Канта находится в Калининграде.

 

Любое понятие можно классифицировать по пяти уровням, причем на каждом из уровней возможны только два варианта.

Уровень первый:

Понятия бывают: общие и единичные.

Общие – это понятия, объем которых составляют два или более предмета. Скажем, понятие «цветок» общее, так как в природе существуют не только два цветка, но гораздо больше. Общие понятия, в свою очередь подразделяются на подтипы: регистрируемые и нерегистрируемые. Регистрируемые – это понятия, у которых количество предметов в объеме можно подсчитать. Например, понятие «планета солнечной системы» является регистрируемым, так как количество таких планет вполне поддается счету. Нерегистрируемые – это понятия, у которых количество предметов в объеме нельзя подсчитать. Таким понятием является, к примеру, «электрон».

Единичные – это понятия, объем которых составляет лишь один предмет. Например: «Планета Земля», «река Обь», «первый человек-космонавт», «Алтайский государственный аграрный университет» и т.п.

Уровень второй:

Понятия бывают: собирательные и несобирательные.

Собирательные – это понятия, выражающие не цельный предмет или качество, а совокупность однотипных предметов. Такими понятиями будут «созвездие», «букет», «взвод» и т.п., так как все эти понятия подразумевают не один предмет, а их группу.

Несобирательные – это понятия, выражающие цельный предмет или качество. Например: «Стол», «радость», «студент» и т.д. Не стоит путать собирательное понятие и собранный предмет. Так, стол может быть собран, но является несобирательным понятием.

Уровень третий:

Понятия бывают: абстрактные и конкретные.

Абстрактные – это понятия, которые выражают не предмет, а лишь качество, присущее какому-либо предмету (abstractio - «отвлечение», латынь). Качества не могут существовать отдельно от предметов, обладающих ими. Таковыми будут понятия «вес», «красота», «добро», «грусть» и т.п.

Конкретные – это понятия, выражающие определенный предмет, даже если его существование не доказано. Например: «Человек», «береза», «призрак», «инопланетянин». Прилагательные и причастия также включаются в конкретные понятия, допустим, «красивый», «кричащий» и т.п.

Уровень четвертый:

Понятия бывают: отрицательные и положительные.

Отрицательные – это понятия, подразумевающие отсутствие чего-либо. Часто идея отсутствия выражается с помощью отрицательных частиц: - не, - без, - а. «Не счастье», «не удача», «без работица», «бес честность», «а моральный поступок» - примеры отрицательных понятий.Однако такое бывает не всегда, иногда прямой смысл слов тоже отражает отсутствие чего-то: «сирота», «вдова» и т.п.

Положительные – это понятия, которые попросту называют предмет (без идеи отсутствия). Например: «Дерево», «студентка», «автомобиль». Нельзя путать отрицательность в логическом и этическом смыслах. В логике отрицательно то, что указывает на отсутствие, в этике – то, что «плохо» или «хорошо». Скажем, понятие «трезвый» является отрицательным в логическом смысле (так как фактически означает «не пьяный»), но положительным в этическом смысле. И, напротив, понятие «убийство» является положительным в логическом смысле (так как не выражает идею отсутствия чего-либо), но отрицательным в этическом смысле.

 

Это интересно: Вопросы этики не раз вставали перед логиками. Так, средневековый индийский логик Удаяна (X-XI вв.), поклонявшийся Кришне, в своей жизни участвовал в очень многих публичных спорах. Такие диспуты часто проходили при дворах индийских царей, и ставкой в них нередко была жизнь проигравшего оппонента. Удаяна неизменно побеждал, а его соперников казнили, то скидывая в пропасть, то привязывая к двум согнутым деревьям или разбегающимся скакунам. Наконец, когда у него уже не осталось противников, Удаяна пришел в храм Кришны, чтобы предложить ему плоды своих усилий. Но двери храма внезапно закрылись перед ним, и так случалось всегда, как только он подходил к храму. Удаяна взмолился: «О, Господь, ведь я именно ради Тебя проповедовал Твое учение!». На что незримый голос ответил: «Ты не проповедовал, Ты попросту убивал!!!» Долгие годы пришлось Удаяне вымаливать прощение и глубоко осознать пагубность своей практики перед тем, как его все-таки пустили в храм. Таким образом, логика отнюдь не исчерпывает жизни человека, также нужно быть этичным человеком.

 

Уровень пятый:

Понятия бывают: соотносительные и безотносительные. Соотносительные – это понятия, которые по своему смыслу подразумевают наличие еще одного или нескольких предметов или выражают связь между ними. Соотносительность может быть нескольких видов. Так, соотносительными будут понятия, выражающие смысловую пару, в которой ни одно из понятий не может по смыслу существовать без другого, при его отсутствии оно теряет свой смысл. Это более или менее очевидная мысль. Например, если человек услышит понятие «муж», то понятие, составляющее с ним пару, сразу приходит на ум – «жена», и наоборот. Другие примеры: «родитель-ребенок», «слуга-господин» и т.п. Также соотносительными будут понятия, выражающие идею связи между двумя или более подобными друг другу предметами. Понятие «дружба» выражает связь между друзьями, «любовь» – между возлюбленными, «родство» – между родственниками и т.д. Соотносительными будут понятия, по своему смыслу предполагающие обязательное существование хотя бы одного подобного же предмета. «Одноклассник» – он не может быть один, ведь он кому-то (!) является одноклассником. Другие примеры: «любовник», «брат», сотрудник» и т.п.

Безотносительные – это понятия, которые обладают смыслом сами по себе. Например: «Карандаш», «шоколад», «озеро». Понятия, обозначающие противоположности («добро-зло»), часть и целое («стул-ножка»), причину и следствие («семечко-плод»), живое и неживое («водитель-машина») являются безотносительными.

А теперь давайте немного потренируемся. Возьмем несколько понятий и «прогоним» их по уже известным нам пяти уровням.

Алтайский университет

 

• общее (регистрируемое)

• несобирательное

• конкретное

• положительное

• безотносительное

безумие

 

• общее (нерегистрируемое)

• несобирательное

• абстрактное

• отрицательное

• безотносительное

 

СССР

 

• единичное

• собирательное

• конкретное

• положительное

• соотносительное

 

Отношения между понятиями

Вся наша жизнь буквально соткана из отношений, именно через отношения с другими людьми мы можем оценить, насколько интересен нам тот, либо иной человек. В логике также придается большое значение выяснению отношений между понятиями. Благодаря этому, мы сможем более грамотно формулировать свою мысль, использовать навыки речевой коммуникации и т.д., что, в конце концов, отразится и на наших отношениях с другими людьми.

Все понятия, прежде всего, можно подразделить на два типа: сравнимые и несравнимые.

Сравнимые – это понятия, у которых в наличии есть хотя бы один общий существенный признак. К примеру, понятия «кот» и «кит» обладают общим существенным признаком – млекопитающее. Несравнимые – это понятия, у которых в наличии нет ни одного общего существенного признака. Например, «время» и «океан».

Сравнимые понятия, в свою очередь, подразделяются на два подтипа: совместимые и несовместимые.

Совместимые – это понятия, объемы которых каким-то образом соприкасаются. Совместимость бывает трех типов.

Равнообъемность – это отношения между понятиями, при котором объемы двух или более понятий полностью совпадают. Примеры: «супруга-жена», «бегемот-гиппопотам» и т.п. Для каждого из типов отечественный мыслитель, логик и математик Л. Эйлер разработал наглядные круговые схемы, которые впоследствии получили название «круги Эйлера», где A – это первое понятие, а B – второе. Отношение равнообъемности имеет следующую схему:

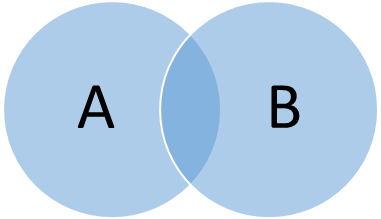
Пересечение – это отношение между понятиями, при котором объемы двух или более понятий частично совпадают. Примеры: «студент-спортсмен», «девушка-россиянка» и т.п. Отношение пересечения Л.Эйлер представил следующей схемой:

 

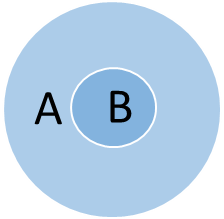
Подчинение – это отношение между понятиями, при котором объем одного понятия полностью включается в объем другого. Примеры: «роза-цветок», «диван-мебель» и т.п. Отношение подчинения графически обозначается таким образом:

 

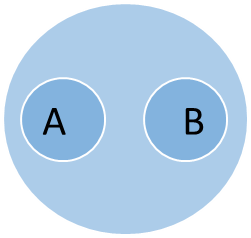
Несовместимые понятия – это понятия, объемы которых никоим образом не соприкасаются. Несовместимость также бывает трех типов.

Соподчинение – это отношение между понятиями, при котором объемы двух или более несовместимых понятий полностью включаются в объем третьего понятия. Примеры: «роза-одуванчик» (третье общее понятие – «цветок»), «диван-сервант» (третье общее понятие – «мебель») и т.п.

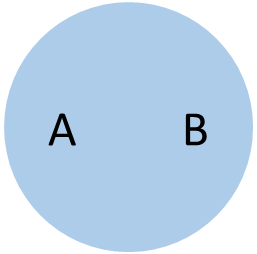
Противоположность – это отношение между понятиями, при котором два несовместимых понятия обладают взаимоисключающими признаками и, входя в объем третьего понятия, полностью не исчерпывают его. Примеры: «трус-смельчак», «белый-черный» и т.п.

 

 

 

Противоречие – это отношение между понятиями, при котором два несовместимых понятия обладают взаимоисключающими признаками и, входя в объем третьего понятия, полностью исчерпывают его. Примеры: «счастье-несчастье», «больной-здоровый» и т.п.

 

 

Это интересно: Л. Эйлер (1707-1783), разработавший круговые схемы для отображения отношений между понятиями, в течение своей весьма насыщенной жизни жил в трех странах: Швейцарии, России, Пруссии, затем снова в России. Во время семилетней войны (1756-1763) России с Пруссией Эйлер проживал в пригороде Берлина, и его дом разнесло попавшим в него «русским» ядром. Фельдмаршал Салтыков тут же возместил урон, а императрица Елизавета прислала 4 тыс. рублей. В 1962 году Екатерина II лично пригласила Эйлера снова в Россию, пообещав оклад в 1800 рублей в год. Эйлер поднял сумму до 3000, и императрица покорно приняла условия. Известно, что еще в первое пребывание в России Эйлер составил гороскоп Ивана VI, в деталях предсказав его трудную судьбу: короткое царствование в детстве, долгое заточение и безвременную смерть в 23 года от рук тюремного охранника.

 

Операции с понятиями

Как правило, человека больше интересуют не вопросы о сущности предметов: «Что они из себя представляют?», «Какова их внутренняя структура и внешняя классификация?», а вопросы функциональные: «Что можно делать с этим предметом?», «Какую пользу он способен принести?». Такую же закономерность мы должны отметить и в отношении понятий. Мы гораздо чаще что-то делаем с понятиями, нежели их классифицируем и т.п. Что же можно делать с понятиями? В логике перечисляется большое количество логических операций, которым можно подвергнуть понятия, но основными, безусловно, являются следующие: определение и деление.

Определение – это логическая операция, раскрывающая содержание понятия. Напомним, что в содержание входят существенные признаки предмета (см. выше).

Все определения можно разделить на два вида: реальные и номинальные.

Реальные – это определения, имеющие четкую внутреннюю структуру. В такой структуре обязательно присутствуют два постоянных элемента: определяемое понятие и определяющее понятие.

Определяемое – это понятие, выражающее неизвестное, содержание которого необходимо прояснить. В реальных определениях определяемое понятие всегда ставится слева от тире. Например: «Часы – это прибор, измеряющий время», где «часы» – определяемое.

Определяющее – это понятие, проясняющее содержание неизвестного. В реальных определениях определяющее всегда ставится справа от тире. Например: «Школа – это учебное заведение, дающее начальное и среднее образование», где понятие «учебное заведение, дающее начальное и среднее образование» является определяющим.

Номинальные – это определения, не имеющие четкой структуры и буквально называющие предмет (nomine – «имя», латынь). Например: «Прибор, измеряю