
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойств и состава нефтей и нефтепродуктовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Плотность
При расчете физико-химических свойств нефтепродуктов принято пользоваться относительной плотностью, представляющей собой соотношение плотностей жидкого нефтепродукта и дистиллированной воды при определенных температурах. Обозначают относительную плотность d Часто для технологических расчетов необходимо пересчитывать плотность нефтепродукта от одной температуры к другой. Высокую точность дает формула Д. И. Менделеева в интервале температур от 0 до 50 ˚С: d где d d
Рис 1 График для определения относительной плотности при известной их плотности d
Рис. 2. График для определения относительной плотности жидких нефтепродуктов d
Значения температурной поправки представлены в таблице 1. Для определения плотности жидких нефтепродуктов при высоких температурах можно пользоваться графиками, приведенными на рис. 1 и 2. На рис. 1 на оси абсцисс откладывают известное значение плотности, из этой точки (А) восстанавливают перпендикуляр до пересечения с линией, соответствующей температуре, при которой определена эта плотность (точка В). Затем проводят линию, параллельную близлежащей наклонной кривой, до пересечения (в точке С) с линией температуры, при которой нужно определить плотность. Из точки С: опускают перпендикуляр до пересечения с осью абсцисс и таким образом (в точке D) находят искомую плотность. При пользовании рис. 2 на оси абсцисс откладывают температуру, при которой требуется определить плотность. Затем восстанавливают перпендикуляр до пересечения с кривой заданной плотности d Часто приходится пересчитывать d
где а - средняя температурная поправка. (Из табл. 1)
Таблица 1 Средняя температурная поправка а для подсчета плотности жидких нефтепродуктов к формуле 1
d Среднюю относительную плотность (dсм) смеси жидких фракций находят по правилу аддитивности:
или dсм= где d1, d2, …, dn - относительные плотности компонентов смеси; V1, V2,..., Vn - объемы компонентов, м3; G1, G, …, Gn - массы компонентов, кг. Относительная плотность газа равна отношению массы m газа, занимающего объем V при некоторых температуре и давлении к массе m1 воздуха, занимающего тот же объем V при тех же температуре и давлении:
Если считать газ идеальным то при Т=273,16 ˚К, Р = 1 атм и V = 22,414 мл масса и равна молекулярному весу М газа. В тех же условиях масса 22,414 мл воздуха составляет 28,9 г, откуда относительная плотность газа или пара относительно воздуха:
Абсолютную плотность газов и паров (ρ, г/см3) при 0 ˚С и 760 мм рт. ст. можно найти, зная массу М и объем 1 моль газа (22,414):
При абсолютной температуре Т (˚К) и давлении П (атм) плотность газа (в кг/м3) может быть найдена по формуле:
Используя формулу (7), можно написать:
Молекулярные веса и плотности некоторых газов и жидкостей приведены в табл. 2. Таблица 2 Свойства углеводородных газов и жидкостей
Задачи 1. Определить относительную плотность нефтепродукта d 2. Определить относительную плотность нефтепродукта d 3. Относительная плотность бензиновой фракции d 4. Плотность нефтяной фракции d 5. Определить относительную плотность d 6. Определить относительную плотность нефтепродукта при 250˚С (d 7. Плотность мазута бинагадинской нефти d 8. Плотность нефтяной фракции d 9. Определить относительную плотность смеси, состоящей из 250 кг бензина плотностью d 10. Определить плотность смеси следующего состава (в объемн. %): 25 бензина (d 11. Смесь состоит из 60 кг н-пентана, 50 кг н-гексана и 25 кг н-гептана. Определить среднюю плотность смеси, если для н-пентана d 12. Смесь состоит из трех компонентов: G 13. Определить абсолютную плотность пропана и н-бутана при 760 мм рт. ст. и 0˚С. 14. Определить плотность крекинг-газа при 400 ˚С и 1200 мм рт. ст., если его молекулярный вес равен 30. 15. Определить плотность газа при 200˚С и 1900 мм рт. ст., если его молекулярный вес равен 58. [ОЛ1, 9]
Молекулярный вес
Молекулярный вес является одной из основных физико-химических характеристик нефтей и нефтепродуктов. Им пользуются для вычисления других физико-химических свойств, при технологических расчетах аппаратуры. Между молекулярным весом и температурой кипения нефтяных фракций существует определенная зависимость: чем больше молекулярный вес нефтяной фракции, тем выше ее температура кипения. Учитывая эту зависимость, Б. М. Воинов предложил следующую общую формулу для определения молекулярного веса М нефтяной фракции: М = а + bt + ct2 (10) где t - средняя молекулярная температура кипения фракции, ˚С; а, b и с - коэффициенты. В частности, для парафиновых углеводородов формула Б. М. Воинова имеет вид: М = 60 + 0,3t + 0,001t2 (11) Пример 1. Средняя температура кипения фракции 120 ˚С. Ее молекулярный вес равен: М = 60 + 0, 3 · 120 + 0, 001 (120)2 = 110,4 Формулу Б. М. Воинова уточнил А. С. Эйгенсон, введя характеризующий фактор К. Эта величина определяет химическую природу нефтепродукта. Для парафинистых нефтепродуктов К = 12,5 - 13, для ароматизированных около 10 и менее, для нафтено-ароматических К = 10 - 11. Характеризующий фактор К определяют по формуле:
где Tcp.мол. - средняя молекулярная температура кипения (для узких фракций можно брать среднюю температуру кипения при разгонке по ГОСТ 2177 - 66), ˚К; d Среднюю молекулярную температуру кипения нефтепродукта (tcp.мол,,˚С) можно определить по формуле:
где
С введением характеризующего фактора формула Б. М. Воинова принимает вид: М = (7K - 21,5) + (0,76 - 0,04К)t + (0,003 К - 0, 00245)t2 (14)
Пример 2. Определить среднюю молекулярную температуру кипения и характеризующий фактор К для нефтепродукта с пределами выкипания 85 - 110˚С плотностыо d Решение. Определяем среднюю температуру кипения каждой
Подставляя полученные данные в формулу (13), получаем: tсрмол = 0,21·87, 5+ 0, 10·92,5 + 0,35·97,5+ 0,23·102,5 + 0,11·107,5 = 97,2 ˚С Определяем характеризующий фактор К по формуле (12):
Средний молекулярный вес смеси можно определить, зная мольную долю и молекулярный вес каждого компонента смеси:
где
Молекулярный вес смеси нескольких нефтяных фракций можно определить по формуле:
Молекулярный, вес нефтепродукта можно определить также по формуле Крэга:
Пример 3. Определить средний молекулярный вес смеси бензола с изооктаном, если мольная доля бензола составляет 0,51, изооктана - 0,49. Решение. Молекулярный вес компонентов найдем по таблице 2: для бензола 78, для изооктана 114. Решение. Молекулярный вес компонентов найдем по таблице 2: для бензола 78, для изооктана 114. Подставляя эти значения в формулу 15, получаем:
Пример 4. Смесь состоит из 150 кг бензола и 2500 кг н-октана. Определить средний молекулярный вес смеси. Решение. Используем формулу 16:
Задачи: 16. Смесь состоит из двух компонентов. Масса каждого компонента 1500 кг; молекулярный вес М1 = 100, М2 = 156. Определить средний молекулярный вес смеси. 17. Смесь состоит из 60 кг н-пентана, 40 кг н-гексана и 20 кг н-гептана. Определить средний молекулярный вес смеси. 18. Определить средний молекулярный вес широкой фракции, состоящей из 20% бензина с М = 110, 40% лигроина с М = 150, 20% керосина с М = 200 и 20% газойля с М = 250. 19. Определить средний молекулярный вес узкой фракции прямой перегонки плотностью d 20. Определить средний молекулярный вес нефтепродукта, имеющего среднюю температуру кипения 100˚С и характеризующий фактор К = 11,80. 21. Определить средний молекулярный вес фракции, имеющей плотность d 22. Определить средний молекулярный вес нефтепродукта, имеющего плотность d 23. Определить молекулярный вес нефтяного газа следующего состава:
Давление насыщенных паров
При изучении фракционного состава нефтей и проведении технологических расчетов аппаратуры приходится пересчитывать давление насыщенных паров нефтепродуктов от одной температуры к другой, а также температуру кипения нефтяных фракций от одного давления к другому. Для осуществления таких пересчетов предложены номограммы. Пример 1. Узкая нефтяная фракция при атмосферном давлении имеет среднюю температуру кипения 149˚С. Какова температура кипения этой фракции при 2000 мм. рт. cт.? Решение. По графику на оси ординат находят точку, соответствующую температуре 149˚ С, и из этой точки проводят прямую, параллельную оси абсцисс, до пересечения с вертикальной линией, отвечающей давлению 760 мм рт. cт. Получают точку А, которая легла на искомый луч. Затем от точки, соответствующей давлению 2000 мм. рт. cт., проводят вертикаль до пересечения с найденным лучом в точке В. Из точки В проводят горизонтальную линию, параллельную оси абсцисс, до пересечения со шкалой температур в точке С, Эта точка дает значение искомой температуры кипения — 190 ˚С. Пример 2. При разгонке мазута из колбы Кляйзена температура паров в момент замера была равна 150˚С, а остаточное давление 2 мм рт. ст. Какова температура паров при атмосферном давлении? Решение. Используют номограмму (см. Приложение 5). На левой шкале номограммы отмечают значение температуры 150 ˚С, на правой шкале — значение давления 2 мм рт. ст. Эти точки соединяют прямой и в точке пересечения со шкалой температура кипения при нормальном давлении» (при разгонке из колбы Кляйзена) находят значение искомой температуры — 330 ˚С. Для подсчета давления насыщенных паров узких нефтяных фракций при низких давлениях пользуются формулой Ашворта [1 — 3):
где P — давление насыщенных паров, атм;. Т' — соответствующая температура, К; T0 — температура кипения при атмосферном давлении, К; f (T) — функция температуры Т, выражаемая уравнением:
Функцию f (T) определяют аналогично. Значения функции f (T) для различных температур приведены в Приложении 7.
Пример 3. Узкая нефтяная фракция при атмосферном давлении имеет среднюю температуру кипения 177˚С. Определить температуру кипения этой фракции при 6,4 атм. Решение. Для решения задачи используем уравнение Ашворта (18) и решим его относительно температуры:
По Приложению 7 найдем значение f (T0) для температуры 177˚ С. f( Tp) = 4,009; lg P = lg 6,4 = 0,8075. Подставляя эти значения, получаем: 0,8075
По Приложению 7 путем интерполяции находим искомую температуру: Т = 274 ˚С = 547 К.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 1868; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.123.61 (0.008 с.) |

 , где t1 - температура воды, ˚С; t2 - температура нефтепродукта, ˚С. В СНГ стандартными температурами при определении плотности являются для воды 4 ˚С и для нефтепродуктов 20 ˚С (d
, где t1 - температура воды, ˚С; t2 - температура нефтепродукта, ˚С. В СНГ стандартными температурами при определении плотности являются для воды 4 ˚С и для нефтепродуктов 20 ˚С (d 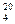 ). В ряде зарубежных стран стандартной температурой для воды и нефтепродукта является 15,6˚С (d
). В ряде зарубежных стран стандартной температурой для воды и нефтепродукта является 15,6˚С (d 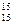 ).
).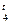 = d
= d 

 ).
).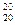 на d
на d 
 (2)
(2) (4)
(4)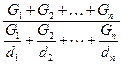 (5)
(5)
 (6)
(6) (7)
(7)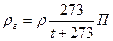 (8)
(8) (9)
(9) , если его d
, если его d  , если его d
, если его d  ) если его d
) если его d 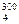 ).
).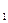 = 459 кг, G
= 459 кг, G  = 711 кг и G
= 711 кг и G  = 234 кг; плотность их d
= 234 кг; плотность их d 
 (12)
(12)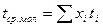 (13)
(13) - средние (арифметические) температур кипения узких фракций, составляющих данный нефтепродукт, ˚С;
- средние (арифметические) температур кипения узких фракций, составляющих данный нефтепродукт, ˚С;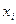 - содержание узких фракций, мол. доли.
- содержание узких фракций, мол. доли.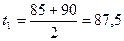 ˚С
˚С 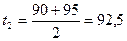 ˚С
˚С ˚С;
˚С;  ˚С;
˚С;  ˚С
˚С
 (15) т.е.
(15) т.е. 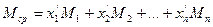
 - содержание компонентов в смеси, мол. доли.
- содержание компонентов в смеси, мол. доли. — молекулярный вес этих компонентов.
— молекулярный вес этих компонентов. (16)
(16) (17)
(17)

 = 0,856.
= 0,856.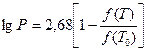 (18)
(18) (19)
(19)




