
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Изменение коэффициентов целевой функции.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
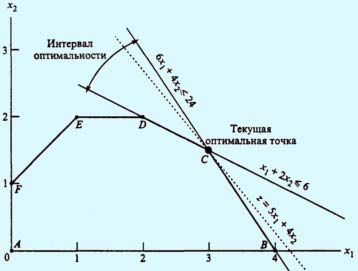
В общем виде целевую функцию задачи ЛП с двумя переменными можно записать следующим образом: Z = с1x1 + с2х2 Изменение значений коэффициентов c1 и c2 приводит к изменению угла наклона прямой z. Графический способ решения задачи ЛП показывает, что это может привести к изменению оптимального решения: оно будет достигаться в другой угловой точке пространства решений. Вместе с тем, очевидно, существуют интервалы изменения коэффициентов c1 и c2, когда текущее оптимальное решение сохраняется. Задача анализа чувствительности и состоит в получении такой информации. В частности, представляет интерес определение интервала оптимальности для отношения c1/c2 (или, что то же самое, для c2/c1); если значение отношения c1/c2 не выходит за пределы этого интервала, то оптимальное решение в данной модели сохраняется неизменным. Следующий пример показывает, как можно получить необходимый результат с помощью анализа графического представления модели ЛП. Пример 1. Применим процедуру анализа чувствительности к модели для компании "Reddy Mikks". На рис. 1 видно, что функция Z = 5х1 + 4х2 достигает максимального значения в угловой точке С.
При изменении коэффициентов целевой функции Z = с1x1 + с2х2 точка С останется точкой оптимального решения до тех пор, пока угол наклона линии z будет лежать между углами наклона двух прямых, пересечением которых является точка С. Этими прямыми являются 6х1 + 4х2 = 24 (ограничение на сырье Ml) и х1 + 2х2 = 6 (ограничение на сырье М2). Алгебраически это можно записать следующим образом:
В первой системе неравенств условие c1 <> 0 означает, что прямая, соответствующая целевой функции, не может быть горизонтальной. Аналогичное условие в следующей системе неравенств означает, что эта же прямая не может быть вертикальной. Из рис. 1 видно, что интервал оптимальности данной задачи (он определяется двумя прямыми, пересекающимися в точке С) не разрешает целевой функции быть ни горизонтальной, ни вертикальной прямой. Таким образом, мы получили две системы неравенств, определяющих интервал оптимальности в нашем примере. (Когда c1 и c2 могут принимать нулевые значения, интервал оптимальности для отношения c1/c2 (или c2/c1) необходимо разбить на два множества, где знаменатели не обращались бы в нуль. Итак, если коэффициенты c1 и c2 удовлетворяют приведенным выше неравенствам, оптимальное решение будет достигаться в точке С. Отметим, если прямая Z = с1x1 + с2х2 совпадет с прямой х1 + 2х2 = 6, то оптимальным решением будет любая точка отрезка CD. Аналогично, если прямая, соответствующая целевой функции, совпадет с прямой 6x1 + 4х2 = 24, тогда любая точка отрезка ВС будет оптимальным решением. Однако заметим, что в обоих случаях точка С остается точкой оптимального решения. Приведенные выше неравенства можно использовать при определении интервала оптимальности для какого-либо одного коэффициента целевой функции, если предположить, что другой коэффициент остается неизменным. Например, если в нашей модели зафиксировано значение коэффициента с2 (пусть с2 = 4), тогда интервал оптимальности для коэффициента с1 получаем из неравенств Аналогично, если зафиксировать значение коэффициента с1 (например, с1 = 5), тогда из неравенств Стоимость ресурсов. Во многих моделях линейного программирования ограничения трактуются как условия ограниченности ресурсов. В таких ограничениях правая часть неравенств является верхней границей количества доступных ресурсов. Рассмотрим чувствительность оптимального решения к изменению ограничений, накладываемых на ресурсы. Такой анализ задачи ЛП предлагает простую меру чувствительности решения, называемую стоимостью единицы ресурса; при изменении количества доступных ресурсов (на единицу) значение целевой функции в оптимальном решении изменится на стоимость единицы ресурса. Проиллюстрируем этот вид анализа задачи ЛП на следующем примере.
Пример 1. В модели для компании "Русские краски" первые два неравенства представляют собой ограничения на использование сырья M1 и М2 соответственно. Определим стоимость единиц этих ресурсов. Начнем с ограничения для сырья M1. Напомним, что в данной задаче оптимальное решение достигается в угловой точке С, являющейся точкой пересечения прямых, соответствующих ограничениям на сырье M1 и М2 (рис. 1).
При изменении уровня доступности материала M1 (увеличение или уменьшение текущего уровня, равного 24 т) точка С оптимального решения "плывет" вдоль отрезка DG. Любое изменение уровня доступности материала M1, приводящее к выходу точки пересечения С из этого отрезка, ведет к неосуществимости оптимального решения в точке С. Поэтому можно сказать, что концевые точки D = (2, 2) и G = (6, 0) отрезка DG определяют интервал осуществимости для ресурса M1. Количество сырья M1, соответствующего точке D = (2, 2), равно 6x1 + 4x2 = 6*2 + 4*2 = 20 т. Аналогично количество сырья, соответствующего точке G = (6, 0), равно 36 т. Таким образом, интервал осуществимости для ресурса M1 составляет 20 ≤ M1 ≤ 36 (здесь через M1 обозначено количество материала M1). Если мы определим М1 как M1 = 24 + D1, где D1 — отклонение количества материала М1 от текущего уровня в 24 т, тогда последние неравенства можно переписать как 20 ≤ 24 + D1 ≤ 36 или -4 ≤ D1 ≤ 12. Это означает, что текущий уровень ресурса M1 может быть уменьшен не более чем на 4 т и увеличен не более чем на 12 т. В этом случае гарантируется, что оптимальное решение будет достигаться в точке С — точке пересечения прямых, соответствующих ограничениям на ресурсы M1 и М2. Теперь вычислим стоимость единицы материала M1. При изменении количества сырья M1 от 20 до 36 тонн, значения целевой функции z будут соответствовать положению точки С на отрезке DG. Обозначив через y1 стоимость единицы ресурса M1, получим следующую формулу:
Если точка С совпадает с точкой D = (2, 2), то z = 5*2 + 4*2 = 18 (тысяч д.e.), если же точка С совпадает с точкой G = (6, 0), тогда z = 5*6 + 4*0= 30 (тысяч д.e.). Отсюда следует, что
Этот результат показывает, что изменение количества ресурса M1 на одну тонну (если общее количество этого ресурса не меньше 20 и не больше 36 тонн) приводит к изменению в оптимальном решении значения целевой функции на 750 д.е. Теперь рассмотрим ресурс М2.
На рис. 2 видно, что интервал осуществимости для ресурса М2 определяется концевыми точками В и H отрезка ВН, где В = (4, 0) и Н= (8/3, 2). Точка Н находится на пересечении прямых ED и ВС. Находим, что количество сырья М2, соответствующего точке В, равно x1 + 2х2 = 4 + 2*0 = 4 т, а точке Н — 8/3+2*2= 20/3 т. Значение целевой функции в точке В равно 5x1 + 4х2 = 5*4 + 4*0 = 20 (тысяч д.e.), а в точке Н — 5*8/3 + 4*2 = 64/3 (тысяч д.e.). Отсюда следует, что количество сырья М2 может изменяться от 4 до 20/3 тонн, а стоимость единицы ресурса М2, обозначенная как у2, равна
Тема 5. Применение симплекс-метода.
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 1462; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.237.54 (0.011 с.) |

 или
или 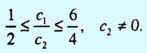
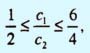 путем подстановки туда значения с2 = 4. После выполнения элементарных арифметических операций получаем неравенства для коэффициента с1: 2 ≤ с1 ≤ 6.
путем подстановки туда значения с2 = 4. После выполнения элементарных арифметических операций получаем неравенства для коэффициента с1: 2 ≤ с1 ≤ 6.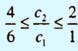 получаем интервал оптимальности для коэффициента с2: 10/3 ≤ с2 ≤ 10.
получаем интервал оптимальности для коэффициента с2: 10/3 ≤ с2 ≤ 10.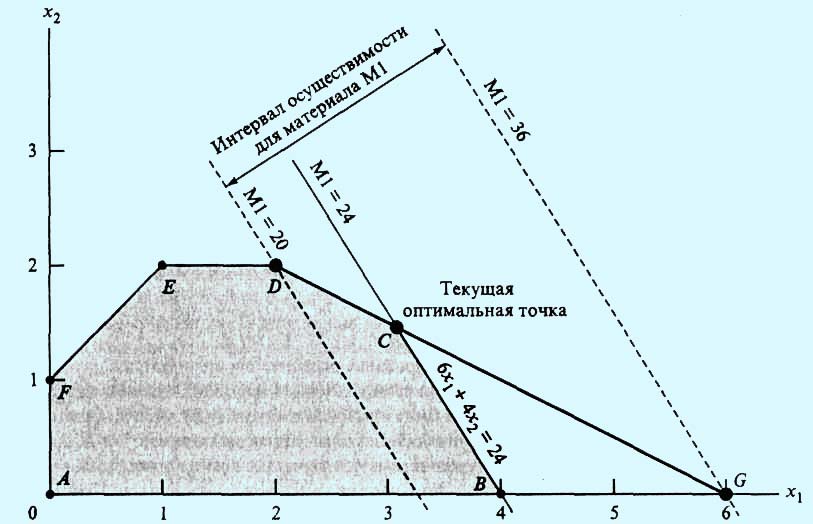

 (тысяч д.е. на тонну материала M1).
(тысяч д.е. на тонну материала M1).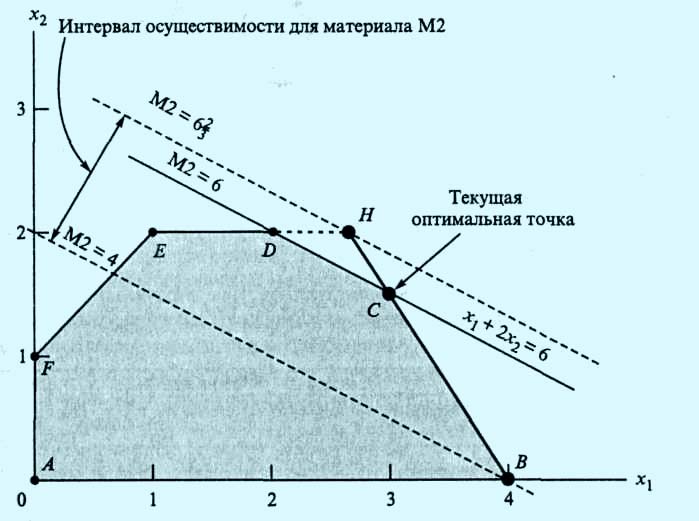
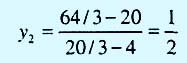 (тысяч д.е. на тонну материла M2).
(тысяч д.е. на тонну материла M2).


