
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Последнее выражение показывает, что величина равна разности между левой и правой частями ограничений двойственной задачи.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Таким образом, все элементы текущей симплекс таблицы вычисляются на основе текущей обратной матрицы В-1 и исходных данных задачи. Пример:
Описываемые вычисления применимы на любом шаге выполнения симплекс-метода. Имеем:
Обратная матрица имеет вид:
Аналогично вычисляются следующие разности: z2 – c2 = -40/3, z3 – c3=0, z4-c4 и z5-c5 = 4/3 +М Коэффициенты равенств, соответствующих ограничениям, вычисляются с использованием обратной матрицы В-1 и вектор-столбцов Рj и b коэффициентов исходных ограничений. Столбец правых частей ограничений на первой итерации симплекс-метода вычисляется следующим образом.
Вычисление столбцов коэффициентов левых частей ограничений:
Столбцы коэффициентов, соответствующие переменным x2, x3, x4, x5 и R вычисляются аналогично. Вывод: Основной вывод заключается в том, что все коэффициенты симплекс-таблицы на любой итерации можно вычислить только на основании соответствующей обратной матрицы В-1 и исходных данных задачи ЛП. Таким образом, при анализе чувствительности оптимального решения конкретной задачи ЛП, где известна обратная матрица В-1 этого решения, можно исследовать эффект от изменения коэффициентов целевой функции и значений правых частей неравенств ограничений посредством новых вычислений всех разностей zj - cj (коэффициенты z-строки) и произведения В-1b (значения правых частей ограничений). Если результаты этих вычислений покажут, что текущее базисное решение остается допустимым и оптимальным, вычисления анализа чувствительности заканчиваются. В противном случае необходимы дополнительные вычисления, возвращающие оптимальность и допустимость исследуемому решению. Тема 8. Анализ чувствительности оптимального решения Оптимальное решение задачи ЛП определяется условиями, которые в реальной жизни не остаются неизменными. В связи с этим особое значение приобретают средства, позволяющие оценить изменения в оптимальном решении, вызванные изменениями в параметрах исходной модели. Таким средством является анализ чувствительности. Он предлагает эффективные вычислительные методы, позволяющие изучить динамическое поведение оптимального решения. Мы уже встречались с анализом чувствительности на элементарном уровне. В этой теме мы подробнее рассмотрим методы анализа чувствительности, основанные на теории двойственности. Двойственная задача – это задача, формулируемая с помощью определенных правил непосредственно из прямой задачи. Анализ чувствительности выполняется уже после получения оптимального решения задачи линейного программирования (ЛП). Его цель — определить, приведет ли изменение коэффициентов исходной задачи к изменению текущего оптимального решения, и если да, то, как эффективно найти новое оптимальное решение (если оно существует). В общем случае изменение коэффициентов исходной задачи может привести к одной из следующих четырех ситуаций.
1. Текущее базисное решение остается неизменным. 2. Текущее решение становится недопустимым. 3. Текущее решение становится неоптимальным. 4. Текущее решение становится неоптимальным и недопустимым. Во второй ситуации можно использовать двойственный симплекс-метод для восстановления допустимости решения. В третьей ситуации мы используем прямой симплекс-метод для получения нового оптимального решения. В четвертой для получения нового оптимального и допустимого решения следует воспользоваться как прямым, так и двойственным симплекс-методом. Для объяснения различных процедур анализа чувствительности используем модель фабрики игрушек TOYCO. Фабрика TOYCO собирает три вида детских игрушек: модели поездов, грузовиков и легковых автомобилей. Сборка модели каждого вида требует последовательного применения трех операций. В задаче необходимо определить объемы производства каждого вида игрушек, максимизирующие общий доход. Для удобства изложения материала повторим формулировки прямой и двойственной задач (табл.2.1).
Таблица 2.1. Приведем симплекс-таблицу, содержащую оптимальное решение прямой задачи. Таблица 2.2. Базис
Изменения, влияющие на допустимость решения. К недопустимости текущего оптимального решения может привести (1) изменение правых частей ограничений (т.е. изменение элементов вектора Изменение элементов вектора Предположим, что фабрика игрушек TOYCO планирует расширить производство своей продукции путем увеличения возможностей сборочных линий на
Таким образом, текущие базисные переменные Хотя новое решение и приводит к увеличению дохода фабрики, реализация мероприятий, необходимых для такого наращивания производства, требует определенного времени. Временной альтернативой такой модернизации производства может служить «перенос» неиспользуемого фонда рабочего времени третьей операции (
Полученное решение не является допустимым, поскольку теперь Базис
В соответствии с двойственным симплекс-методом исключаемой переменной будет Базис
По существу, оптимальное решение осталось неизменным. Это означает, что в данном случае «перенос» части фонда рабочего времени третьей операции в фонд рабочего времени первой операции не приводит к улучшению целевой функции. Интервалы допустимых изменений для элементов вектора Пусть в задаче о фабрике игрушек TOYCO нас интересует интервал допустимости для значения фонда рабочего времени первой операции. Заменим вектор
Переменная
Первое неравенство
или
Изменения значения целевой функции, соответствующее изменение Чтобы проиллюстрировать использование данного интервала допустимости, предположим, что фонд рабочего времени первой операции изменился от
Для вычисления нового значения целевой функции сначала найдем значения двойственных цен.
Таким образом, стоимость одной минуты фонда рабочего времени первой операции равна
|
||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 619; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.221.124 (0.011 с.) |






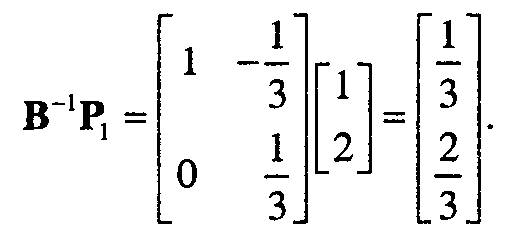
 при ограничениях
при ограничениях
 , (операция 1)
, (операция 1)
 , (операция 2)
, (операция 2)
 , (операция 3)
, (операция 3)
 .
.

 при ограничениях
при ограничениях
 ,
,
 ,
,
 ,
,
 .
.







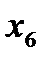 Решение
Решение



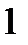



























 ) и (2) введение в множество ограничений задачи нового ограничения. В любом случае недопустимость решения проявится в том, что, по крайней мере, один элемент в векторе
) и (2) введение в множество ограничений задачи нового ограничения. В любом случае недопустимость решения проявится в том, что, по крайней мере, один элемент в векторе 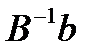 станет отрицательным, т.е. одна или несколько базисных переменных примут отрицательные значения.
станет отрицательным, т.е. одна или несколько базисных переменных примут отрицательные значения. правых частей ограничений. В следующем примере проиллюстрирован подход к исследованию ситуации, когда изменяется несколько элементов вектора Ь, содержащего значения правых частей ограничений.
правых частей ограничений. В следующем примере проиллюстрирован подход к исследованию ситуации, когда изменяется несколько элементов вектора Ь, содержащего значения правых частей ограничений. , что даст следующий фонд рабочего времени для каждого вида сборочной операции:
, что даст следующий фонд рабочего времени для каждого вида сборочной операции: 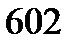 ,
,  и
и  минут соответственно. Эти изменения влияют только на правые части неравенств ограничений. По формуле
минут соответственно. Эти изменения влияют только на правые части неравенств ограничений. По формуле  найдем новое решение задачи.
найдем новое решение задачи.
 ,
,  и
и  с новыми значениями
с новыми значениями  ,
,  и
и  по-прежнему составляют допустимое решение. Соответствующее этому решению оптимальное значение целевой функции (максимальный доход) равно
по-прежнему составляют допустимое решение. Соответствующее этому решению оптимальное значение целевой функции (максимальный доход) равно  .
. минут) в фонд первой. Тогда фонд рабочего времени трех сборочных операций будет равен
минут) в фонд первой. Тогда фонд рабочего времени трех сборочных операций будет равен  ,
,  и
и 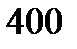 минут соответственно. С учетом новых ограничений получаем следующее решение.
минут соответственно. С учетом новых ограничений получаем следующее решение.
 . Для возврата в область допустимых решений применим двойственный симплекс-метод. Сначала изменим значения в столбце «Решение» симплекс-таблицы (эти новые значения выделены в следующей симплекс-таблице). Отметим, что соответствующее значение целевой функции равно
. Для возврата в область допустимых решений применим двойственный симплекс-метод. Сначала изменим значения в столбце «Решение» симплекс-таблицы (эти новые значения выделены в следующей симплекс-таблице). Отметим, что соответствующее значение целевой функции равно  .
.




 Решение
Решение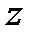



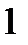








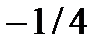







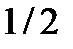









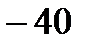
 , а вводимой –
, а вводимой – 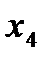 . В результате получим следующую симплекс-таблицу с оптимальным допустимым решением. (В общем случае для получения допустимого решения может потребоваться несколько итераций двойственного симплекс-метода).
. В результате получим следующую симплекс-таблицу с оптимальным допустимым решением. (В общем случае для получения допустимого решения может потребоваться несколько итераций двойственного симплекс-метода).



 Решение
Решение






















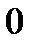





 . Другой способ исследования влияния изменения доступности ресурсов (т.е. элементов вектора
. Другой способ исследования влияния изменения доступности ресурсов (т.е. элементов вектора  правых частей неравенств ограничений) заключается в определении интервалов допустимости для этих элементов, сохраняющих текущее решение допустимым. Следующий пример иллюстрирует метод анализа чувствительности.
правых частей неравенств ограничений) заключается в определении интервалов допустимости для этих элементов, сохраняющих текущее решение допустимым. Следующий пример иллюстрирует метод анализа чувствительности. вектором
вектором .
. представляет изменения фонда рабочего времени первой операции по сравнению с текущим уровнем в
представляет изменения фонда рабочего времени первой операции по сравнению с текущим уровнем в  минут. Для того чтобы текущее базисное решение осталось недопустимым, необходимо выполнение неравенства
минут. Для того чтобы текущее базисное решение осталось недопустимым, необходимо выполнение неравенства  . Отсюда получаем следующую систему неравенств.
. Отсюда получаем следующую систему неравенств. .
. порождает
порождает  , второе неравенство
, второе неравенство  не зависит от
не зависит от  , третье
, третье  дает условие
дает условие  . Таким образом, текущее базисное решение останется допустимым при выполнении неравенств
. Таким образом, текущее базисное решение останется допустимым при выполнении неравенств  . Это эквивалентно следующему интервалу допустимости для фонда рабочего времени первой операции.
. Это эквивалентно следующему интервалу допустимости для фонда рабочего времени первой операции. Фонд рабочего времени операции
Фонд рабочего времени операции 
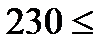 Фонд рабочего времени операции
Фонд рабочего времени операции 
 , равно
, равно  , где
, где  – стоимость (в долларах) одной минуты фонда рабочего времени первой операции (т.е. двойственная цена этого ресурса).
– стоимость (в долларах) одной минуты фонда рабочего времени первой операции (т.е. двойственная цена этого ресурса). до
до  минут. Текущее базисное решение остается допустимым, поскольку новое значение фонда рабочего времени первой операции принадлежит интервалу допустимости. Для вычисления новых значений переменных воспользуемся значением
минут. Текущее базисное решение остается допустимым, поскольку новое значение фонда рабочего времени первой операции принадлежит интервалу допустимости. Для вычисления новых значений переменных воспользуемся значением  . Далее получим следующее.
. Далее получим следующее. .
. .
. . Тогда изменение оптимального дохода составит
. Тогда изменение оптимального дохода составит  . Следует помнить, что данная стоимость минуты фонда рабочего времени первой операции, равная
. Следует помнить, что данная стоимость минуты фонда рабочего времени первой операции, равная  , справедлива только для указанного выше интервала изменения
, справедлива только для указанного выше интервала изменения  . Любое изменение, выходящее за этот интервал, приводит к недопустимому решению. В таком случае следует использовать двойственный симплекс-метод для нахождения нового решения, если оно существует.
. Любое изменение, выходящее за этот интервал, приводит к недопустимому решению. В таком случае следует использовать двойственный симплекс-метод для нахождения нового решения, если оно существует.


