Алгоритм построения минимального остовного дерева.

Минимальное остовное дерево (или минимальное покрывающее дерево) в связанном, взвешенном, неориентированном графе — это остовное дерево этого графа, имеющее минимальный возможный вес, где под весом дерева понимается сумма весов входящих в него рёбер.

Алгоритм построения минимального остовного дерева предполагает соединение всех вершин сети с помощью путей наименьшей длины. Типичной задачей, для решения которой необходим такой алгоритм, является создание (проектирование) сети дорог с твердым покрытием, соединяющих населенные пункты в сельской местности, где дороги, соединяющие два каких-либо пункта, могут проходить через другие населенные пункты. Наиболее экономичный проект дорожной системы должен минимизировать общую длину дорог с твердым покрытием, при этом желаемый результат можно получить с помощью алгоритма построения минимального остовного дерева.

Рассмотрим общую схему работы алгоритмов построения минимального остовного дерева с использованием жадной стратегии. Итак, пусть дан связный неориентированный граф G (V; E) c n вершинами и весовая функция w: E → R.

Искомый остов строится постепенно. Алгоритм использует некоторый ациклический подграф А исходного графа G, который называется промежуточным остовным лесом. Изначально G состоит из n вершин-компонент, не соединенных друг с другом (n деревьев из одной вершины). На каждом шаге в A добавляется одно новое ребро. Граф A всегда является подграфом некоторого минимального остова. Очередное добавляемое ребро e =(u, v) выбирается так, чтобы не нарушить этого свойства: A ∪ { e } тоже должно быть подграфом минимального. Такое ребро называется безопасным.

Опишем процедуру выполнения этого алгоритма. Обозначим через N={1,2,…,n} множество узлов сети и введем новые обозначения:

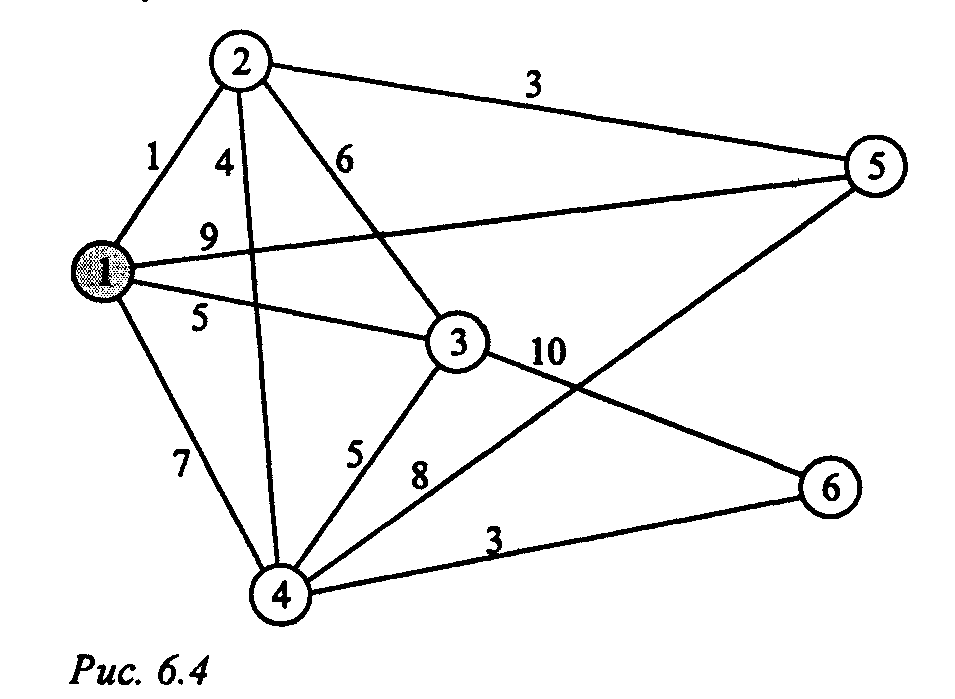
Пример построения:

Телевизионная компания планирует подключение к своей кабельной сети пяти новых районов. На рис. 6.4 показана структура планируемой сети и расстояния (в милях) между районами и телецентром. Необходимо спланировать наиболее экономичную кабельную сеть.

 

 

Чтобы начать выполнение алгоритма построения минимального остовного дерева, выберем узел 1 (или любой другой узел). Тогда

Последовательные итерации выполнения алгоритма представлены на рис. 6.5. Здесь тонкими линиями показаны ребра, соединяющие узлы, принадлежащие множествам , среди которых ищется ребро с минимальной стоимостью (длиной). Это найденное ребро показано пунктирной линией. Толстыми сплошными линиями обозначены ребра, соединяющие узлы множества С_к (и которые ранее обозначались пунктирными линиями).

Например, на первой итерации ребро (1,2) имеет наименьшую стоимость (т.е. наименьшее расстояние между пунктами сети) среди всех других ребер, соединяющих узел 1 с узлами множества , (отметим, что узел 6 не имеет ребра, непосредственно соединяющего его с узлом 1).

Решение в виде минимального остовного дерева получено на 6-й итерации (рис. 6.5).

Минимальная длина кабеля для построения такой сети равна 1 + 3 4- 4 + + 3 + 5 = 16 милям.

 

Тема 10. Задача нахождения кратчайшего пути

Задача нахождения кратчайшего пути:

Определение в транспортной сети кратчайшего пути между заданным исходным пунктом и пунктом назначения. Такую модель можно использовать для описания разнообразных ситуаций, как показано в следующих примерах.

Практические примеры задачи нахождения кратчайшего пути.

Пример 1: Замена оборудования

Компания по прокату автомобилей разрабатывает план по обновлению парка своих машин на следующие пять лет (2001-2005 гг.) Каждый автомобиль должен проработать не менее одного и не более трех лет. В следующей таблице приведена стоимость замены автомобиля в зависимости от года покупки и срока эксплуатации.

Задачу можно сформулировать как сетевую с пятью узлами с номерами от 1 до 5,

соответствующими годам 2001-2005. Из узла 1 (2001 год) дуги идут только к узлам 2, 3 и 4, поскольку автомобиль может эксплуатироваться не менее одного и не более трех лет. Дуги из других узлов интерпретируются аналогично.

Стоимости дуг равны стоимостям замены автомобилей. Решение задачи эквивалентно нахождению кратчайшего пути между узлами 1 и 5.

На рис. 6.9 показана построенная сеть. С помощью программы TORA находим кратчайший путь 1—>3—>5 (показан на рис. 6.9 жирными линиями). Это решение означает, что втомобили, приобретенные в 2001 году (узел 1), будут эксплуатироваться 2 года, до 2003 года (узел 3), затем они будут заменены новыми, которые будут эксплуатироваться до конца 2005 года. Общая стоимость замены составит 5400+ 7100 =12 500 долл.

Пример 2: Самый надежный маршрут

М-р Разумник ежедневно ездит на работу на автомобиле. Закончив в свое время полный курс по теории исследования операций, он легко определил самый короткий путь от дома до работы. К сожалению, данный маршрут усиленно патрулируется нарядами полиции, и автомобиль Разумника часто останавливают за превышение скорости (как ему кажется, не обоснованно). Таким образом, самый короткий путь оказался не самым быстрым. Поэтому м-р Разумник планирует разработать новый маршрут, на котором он имел бы самую высокую вероятность не быть остановленным полицией.

Схема сети дорог, по которой м-р Разумник может добраться от дома до работы, показана на рис. 6.10. На этой же схеме приведены вероятности не быть остановленным для каждого сегмента сети дорог. Вероятность не быть остановленным на всем пути следования автомобиля Разумника равна произведению вероятностей не быть остановленным на каждом сегменте выбранного пути. Например, вероятность не быть остановленным на маршруте

1-»3-»5-»7 равна 0,9 х 0,3 х 0,25 = 0,0675.