Стандартная форма задачи ЛП и ее базисные решения.

Для решения задач, которые содержат более 2 переменных, разработан специальный алгебраический метод. В основе него лежит следующий принцип: предполагается, что оптимальному решению соответствует одна из крайних точек допустимого множества, следовательно, необходимо провести оценку значений целевой функции во всех крайних точках допустимого множества и выбрать ту из них, в которой достигается оптимальное значение целевой функции. Переход от одной крайней точки допустимого множества к другой осуществляется тогда, когда значения целевой функции уменьшаются. Если окажется, что некоторое базисное решение улучшить уже нельзя, оно является оптимальным планом задачи.

Стандартная форма задачи ЛП.

Стандартная форма задачи ЛП предполагает выполнение следующих требований:

1. Все ограничения (включая ограничения неотрицательности переменных) преобразуются в равенства с неотрицательной правой частью.

2. Все переменные неотрицательны.

3. Целевую функцию следует или максимизировать, или минимизировать.

 

1. Преобразование неравенств в равенства.

Неравенства любого типа (со знаками >= или <=) можно преобразовать в равенства путем добавления в левую часть неравенств дополнительных переменных – остаточных или избыточных. В неравенствах она различаются тем, что перед остаточными переменными стоит знак «+», а перед избыточными переменными знак «-».

Пример неравенства типа “≤”. Для неравенств такого типа в левую часть неравенства вводится неотрицательная остаточная переменная. Например, в модели компании Reddy Mikks

ограничение на количество сырья Ml задается в виде неравенства 6х₁ + 4х₂ ≤ 24. Вводя новую неотрицательную переменную s₁,которая показывает остаток (неиспользованное количество) сырья Ml, это ограничение преобразуется в равенство

6х₁ + 4х₂ + s₁ = 24, s₁ ≥ 0.

Пример неравенства типа “≥”. Неравенства такого типа в задачах ЛП обычно устанавливают нижнюю границу чего-либо. Избыточная переменная определяет превышение значения левой части неравенства над этой границей. Так, в модели "диеты" неравенство

х₁ + х₂ ≥ 800 показывает, что суточное производство пищевой добавки не должно быть меньше 800 фунтов. Математически это неравенство эквивалентно х₁ + х₂ – S₁= 800, S₁ ≥0.

Положительное значение избыточной переменной S₁, показывает превышение суточного производства добавки над минимальным значением в 800 фунтов.

Важно еще раз подчеркнуть, что дополнительные переменные — остаточная и избыточная — всегда неотрицательные.

Правую часть равенства всегда можно сделать неотрицательной, умножив все равенство на -1. Кроме того, заметим, что неравенство типа "≤" также преобразуется в неравенство типа "≥" посредством умножения обеих частей неравенства на -1.

Например, неравенство -х₁ + х₂ ≤ -3 эквивалентно равенству - х₁ + х_{2 +} S₁= -3, S₁ ≥ 0.

Теперь, умножая обе части этого равенства на -1, получим равенство с неотрицательной правой частью:

х_{1 -} х_{2 -} S₁= 3

2. Преобразование свободных переменных в неотрицательные.

Свободную переменную x_j (т.е переменную, которая может принимать как отрицательные, так и положительные значения) можно представить как разность двух неотрицательных переменных следующим образом:

x_j = x_j⁺ - x_j^-

Например, для x_j = -5 положим x_j⁺ =0 и x_j^- =5. Если же для x_j = +5, тогда x_j⁺ =5 и x_j^- =0. В обоих случаях переменные x_j⁺ и x_j^- неотрицательны.

Такое преобразование свободных переменных следует выполнить во всех неравенствах и в целевой функции. После решения задачи с переменными x_j⁺ и x_j^- значения исходных переменных восстанавливаются с помощью обратной подстановки.

3.Преобразование задачи максимизации в задачу минимизации.

Задача максимизации функции F(x₁, x₂, …, x_n) эквивалентна минимизации функции F(x₁, x₂, …, x_n), поскольку при решении обеих задач предоставляется один и тот же набор значений переменных x₁, x₂, …, x_n.

Пример: Преобразуем следующую задачу ЛП в стандартную форму.

Максимизировать z = 2x₁ + 3x₂ + 5x₃

При выполнении условий

x₁ + x₂ - x₃ ≥ -5,

-6x₁ + 7x₂ - 9x₃ ≤ 4,

x₁ + x₂ +4 x₃ = 10,

x_1,x₂ ≥ 0,

x₃ – свободная переменная.

Для преобразования задачи в стандартную форму нужно:

1. Вычтем из левой части первого неравенства дополнительную (избыточную) переменную S₁ и затем умножим все неравенства на -1, для того, чтобы правая часть неравенства стала положительной. (Другой путь преобразования неравенства: сначала умножим его на -1 – неравенство примет вид «≤» вместо «≥», далее к левой части неравенства прибавим дополнительную (остаточную) переменную S₁).

2. Добавим дополнительную (остаточную) переменную S₂, к левой части второго неравенства.

Так как третье ограничение изначально записано в виде равенства, то оставляем его без изменений.

4. Выполняем замену x_{3 =} x₃⁺ _- x₃^-, где x₃⁺_, x₃^- ≥0 во всех ограничениях и целевой функции.

Получаем следующую стандартную задачу ЛП.

Максимизировать z = 2x₁ + 3x₂ + 5x₃⁺ _- 5x₃^-

При выполнении условий

- x_{1 -} x₂ + x₃⁺ - x₃^- + x₄ = 5,

-6x₁ + 7x₂ - 9x₃⁺ + 9 x₃^- + x₅ = 4,

x₁ + x₂ +4 x₃ ⁺ - 4 x₃ ^- = 10,

x_1, x_2, x₃ ⁺, x₃ ^- _, x_4, x₅≥ 0,

x₃ – свободная переменная.

Определения базисных решений.

Задача ЛП, записанная в стандартной форме, содержит m линейных равенств с n неизвестными переменными (m < n). Разделим n переменных на два множества: (1) n – m переменные, которые положим равными нулю, и (2) оставшиеся m переменные, значения которых определяются как решение системы из m линейных уравнений. Если это решение единственное, то соответствующие m переменные называются базисными, а остальные n – m нулевые переменные – небазисными. В этом случае результирующие значения переменных составляют базисное решение. Если все переменные принимают неотрицательные значения, то такое базисное решение является допустимым. В противном случае – недопустимым.

Основываясь на этих определениях, нетрудно подсчитать, что количество всех положительных базисных решений для m уравнений с уравнений с n неизвестными не превосходит:

Пример: Рассмотрим следующую систему 2-х уравнений с пятью неизвестными (m=2, n=5)

x₁ + x₂ +4x₃ + 2x₄ + 3x₅ = 8,

4x₁ +2x₂ + 2x₃ + x₄ + 6x₅ = 4.

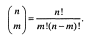
Определим различные решения этой системы. Количество положительных базисных решений равно Ниже покажем, что некоторые из этих решений на самом деле не будут базисными.