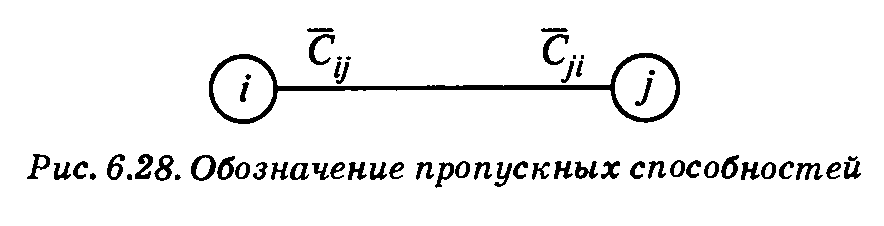Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Таким образом, м-ру разумнику необходимо решить задачу выбора маршрута, который максимизировал бы вероятность не быть остановленным.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
С точки зрения математики задача максимизации вероятности
Пример 3: Головоломка о трех бидонах. Восьмилитровый бидон заполнен некой жидкостью, а два бидона емкостью 5 и 3 литра пусты. Необходимо разделить 8 литров жидкости на две равные части, используя только три имеющихся бидона. Какое минимальное количество переливаний из бидона в бидон надо сделать, чтобы достичь желаемого результата? Вы, вероятно, уже нашли решение этой головоломки. Вместе с тем ее можно решить как задачу о нахождении кратчайшего пути. В этой сетевой модели каждый узел будет соответствовать объемам жидкости в 8-, 5- и 3-литровом бидонах. Начальным узлом будет (8, 0, 0), а конечным — D, 4, 0). Новый узел получается из текущего при однократном переливании жидкости из одного бидона в другой. На рис. 6.12 показаны различные маршруты, ведущие от начального узла (8, 0, 0) к конечному узлу(4, 4, 0). Таким образом, наша головоломка сведена к задаче определения кратчайшего пути между узлами (8, 0, 0) и (4, 4, 0).
Оптимальное решение, показанное в нижней части рис. 6.12, требует семи переливаний из бидона в бидон. Алгоритм нахождения кратчайшего пути. Здесь представлены два алгоритма для решения задачи поиска кратчайшего пути как в сетях, имеющих циклы, так и в сетях, не имеющих циклов: 1. Алгоритм Дейкстры. 2. Алгоритм Флойда. Алгоритм Дейкстры разработан для поиска кратчайшего пути между заданным исходным узлом и любым другим узлом сети. Алгоритм Флойда более общий, поскольку он позволяет одновременно найти минимальные пути между любыми двумя узлами сети. Алгоритм Дейкстры. В процессе выполнения этого алгоритма при переходе от узла i к следующему узлу j, используется специальная процедура пометки ребер. Обозначим через ui кратчайшее расстояние от исходного узла 1 до узла i, через dij — длину ребра (i, j). Тогда для узла j определим метку [ uj, i ] следующим образом:
Метки узлов в алгоритме Дейкстры могут быть двух типов: · временные · постоянные. Временная метка впоследствии может быть заменена на другую временную, если будет найден более короткий путь к данному узлу. Когда же станет очевидным, что не существует более короткого пути от исходного узла к данному, статус временной метки изменяется на постоянный. Вычислительная схема алгоритма состоит из следующих этапов. Этап 0. Исходному узлу (узел 1) присваивается постоянная метка [0, —]. Полагаем i = 1. Этап 1. а). Вычисляются временные метки b). Если все узлы имеют постоянные метки, процесс вычислений заканчивается. В противном случае выбирается метка Пример: На рис. 6.14 показана транспортная сеть, состоящая из пяти городов (расстояния между городами (в милях) приведены возле соответствующих дуг сети). Необходимо найти кратчайшие расстояния от города 1 (узел 1) до всех остальных четырех городов.
Этап 0. Назначаем узлу 1 постоянную метку [0, —]. Этап 1. Из узла 1 можно достичь узлов 2 и 3. Вычисляем метки для этих узлов, в результате получаем следующую таблицу меток.
Среди узлов 2 и 3 узел 3 имеет наименьшее значение расстояния Этап 2. Из узла 3 (последнего узла с постоянной меткой) можно попасть в узлы 4 и 5. Получаем следующий список узлов.
Временный статус метки [40, 3] узла 4 заменяется постоянным Этап 3. Из узла 4 можно достичь узлов 2 и 5. После вычисления меток получим следующий их список. Временная метка [100, 1], полученная узлом 2 на втором этапе, изменена на [55, 4]. Это указывает на то, что найден более короткий путь к этому узлу (проходящий через узел 4). На третьем этапе узел 5 получает две метки с одинаковым значением расстояния u5 = 90. Этап 4. Из узла 2 можно перейти только в узел 3, но он уже имеет постоянную метку, которую нельзя изменить. Поэтому на данном этапе получаем такой же список меток, как и на предыдущем, но с единственным изменением: метка узла 2 получает статус постоянной. С временной меткой остается только узел 5, но, так как из этого узла нельзя попасть ни в какой другой, процесс вычислений заканчивается. Алгоритм позволяет проводить вычисления непосредственно на схеме сети, как показано на рис. 6.15.
Кратчайший маршрут между узлом 1 и любым другим узлом определяется, начиная с узла назначения путем прохождения их в обратном направлении с помощью информации, представленной в постоянных метках. Например, для определения кратчайшего маршрута между узлами 1 и 2 получаем такую обратную последовательность узлов
Алгоритм Флойда. Этот алгоритм более общий по сравнению с алгоритмом Дейкстры, так как он находит кратчайшие пути между любыми двумя узлами сети. В этом алгоритме сеть представлена в виде квадратной матрицы с n строками и n столбцами. Элемент (i, j) равен расстоянию dij от узла i к узлу j, которое имеет конечное значение, если существует дуга (i, j), и равен бесконечности в противном случае. Покажем сначала основную идею метода Флойда. Пусть есть три узла i, j и k и заданы расстояния между ними (рис. 6.19). Если выполняется неравенство
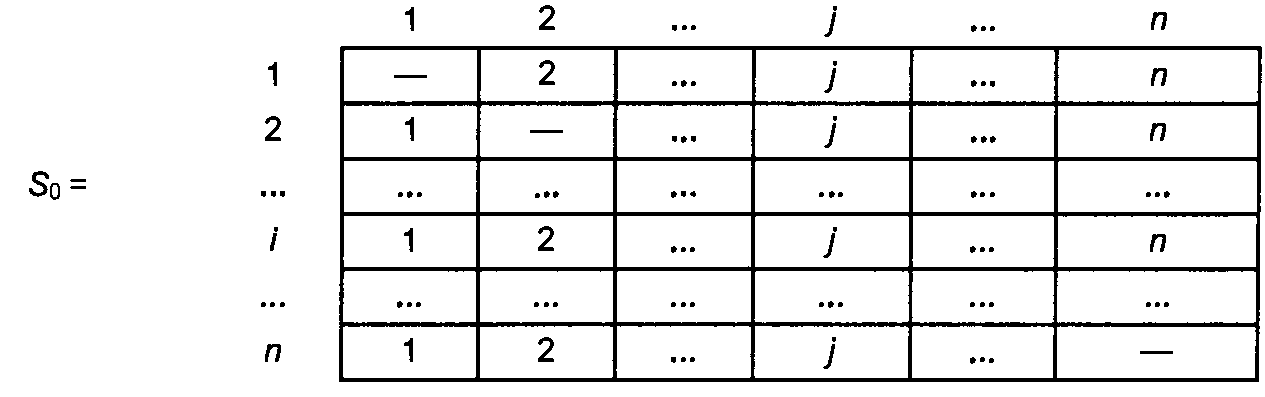
Алгоритм Флойда требует выполнения следующих действий. Этап 0. Определяем начальную матрицу расстояний D0 и матрицу последовательности узлов S0. Диагональные элементы обеих матриц помечаются знаком "—", показывающим, что эти элементы в вычислениях не участвуют. Полагаем k = 1.
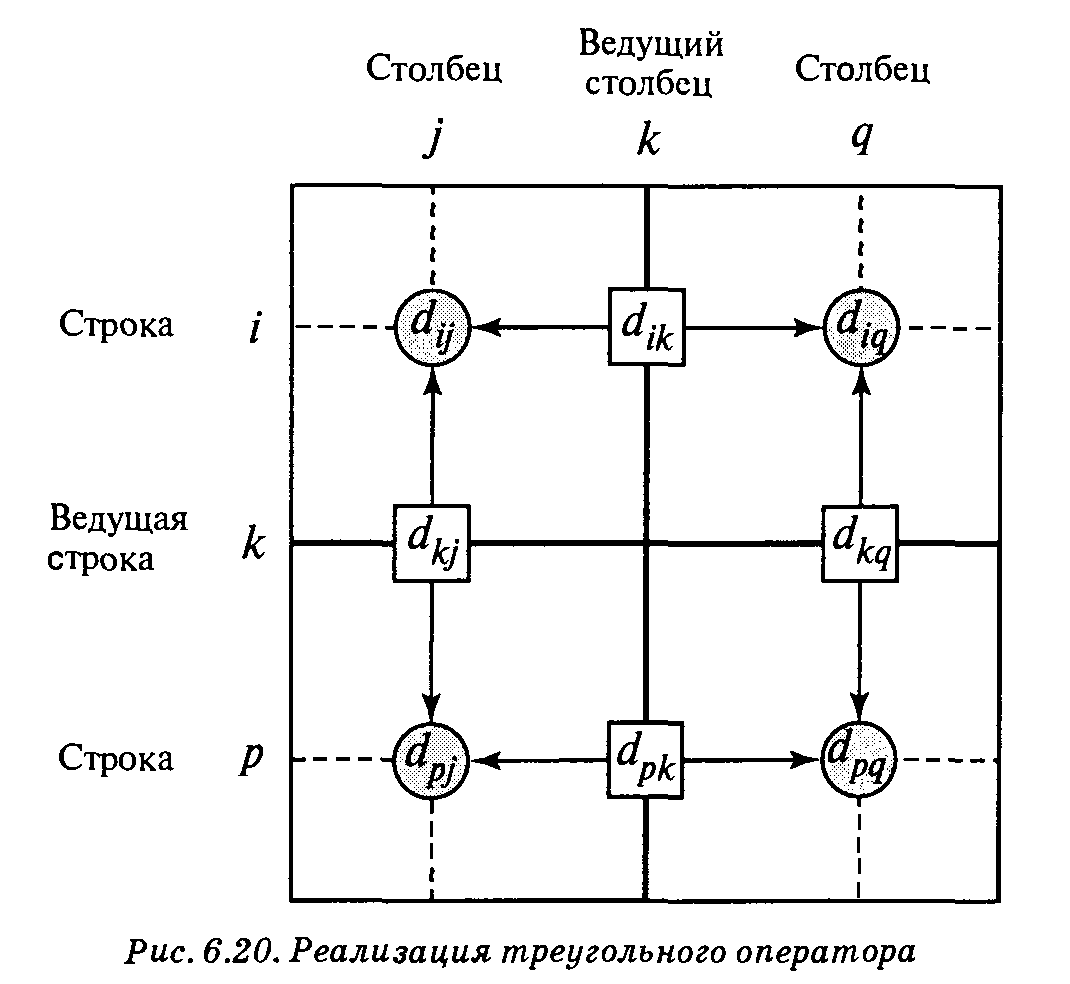
Основной этап k. Задаем строку k и столбец k как ведущую строку и ведущий столбец. Рассматриваем возможность применения треугольного оператора ко всем элементам dij матрицы Dk-1. Если выполняется неравенство
то делаем следующее: a). создаем матрицу Dk путем замены в матрице Dk-1 элемента dij суммой dik + dkj, b). создаем матрицу Sk, меняя в матрице Sk-1 элемент sij на k. Полагаем k = k + l и повторяем этап k. Поясним действия, выполняемые на k-м этапе алгоритма, представив матрицу Dk-l так, как она показана на рис. 6.20. На этом рисунке строка k и столбец k являются ведущими. Строка i — любая строка с номером от 1 до k - 1, а строка р — произвольная строка с номером от k + 1 до n. Аналогично столбец j представляет любой столбец с номером от 1 до k - 1, а столбец q — произвольный столбец с номером от k + 1 до n. Треугольный оператор выполняется следующим образом. Если сумма элементов ведущих строки и столбца (показанных в квадратиках) меньше элементов, находящихся на пересечении столбца и строки (показаны в кружках), соответствующих рассматриваемым ведущим элементам, то расстояние (элемент в кружке) заменяется суммой расстояний, представленных ведущими элементами. После реализации п этапов алгоритма определение по матрицам Dn и Sn кратчайшего пути между узлами i и j выполняется по следующим правилам. 1. Расстояние между узлами i и j равно элементу dij в матрице Dn. 2. Промежуточные узлы пути от узла i к узлу j определяем по матрице Sn. Пусть sij= k, тогда имеем путь i → k → j. Если далее sik = k и skj = j, тогда считаем, что весь путь определен, так как найдены все промежуточные узлы. В противном случае повторяем описанную процедуру для путей от узла i к узлу k и от узла k к узлу j.
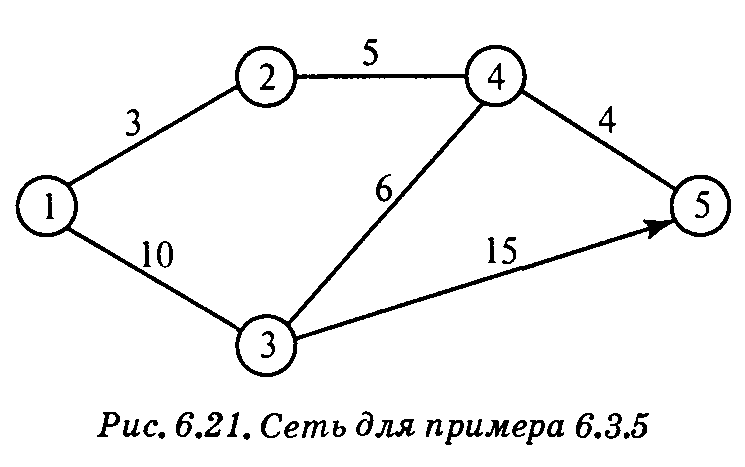
Пример: Найдем для сети, показанной на рис. 6.21, кратчайшие пути между любыми двумя узлами. Расстояния между узлами этой сети проставлены на рисунке возле соответствующих ребер. Ребро (3, 5) ориентированно, поэтому не допускается движение от узла 5 к узлу 3. Все остальные ребра допускают движение в обе стороны.
Этап 0. Начальные матрицы D0 и S0 строятся непосредственно по заданной схеме сети. Матрица D0 симметрична, за исключением пары элементов d35 и d53, где d53 =
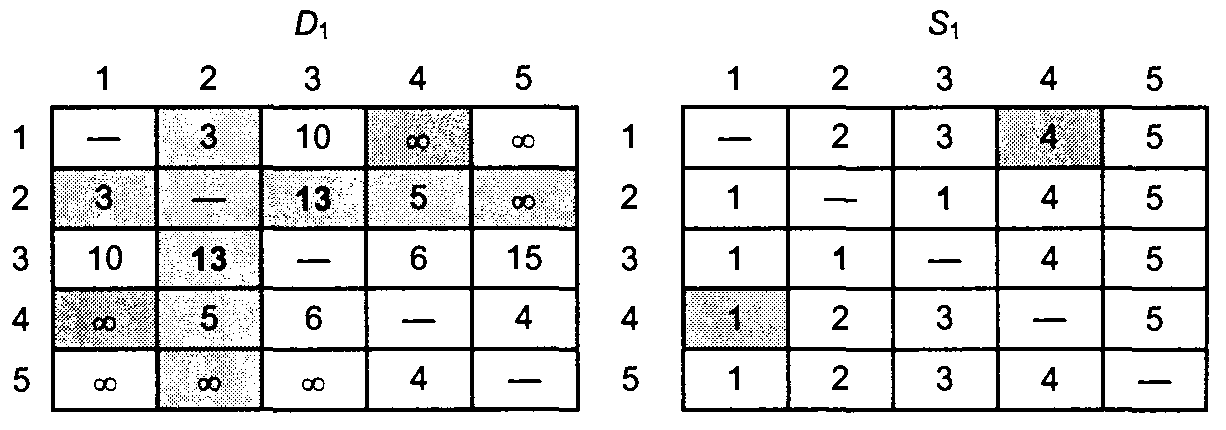
Этап 1. В матрице D0 выделены ведущие строка и столбец с номером k = 1. Затемненными представлены элементы d23 и d32, единственные среди элементов матрицы D0, значения которых можно улучшить с помощью треугольного оператора. Таким образом, чтобы на основе матриц D0 и S0 получить матрицы D1 и S1 выполняем следующие действия. 1. Заменяем d23 на d21 + dl3 = 3 + 10 = 13 и устанавливаем s23 = 1. 2. Заменяем d32 на d3l + dl2 = 10 + 3 = 13 и устанавливаем s32 = 1. Матрицы D1 и S1 имеют следующий вид.
Этап 2. Полагаем k = 2; в матрице D1 выделены ведущие строка и столбец. Треугольный оператор применяется к элементам матриц D1 и S1, выделенным затенением. В результате получаем матрицы D2 и S2.
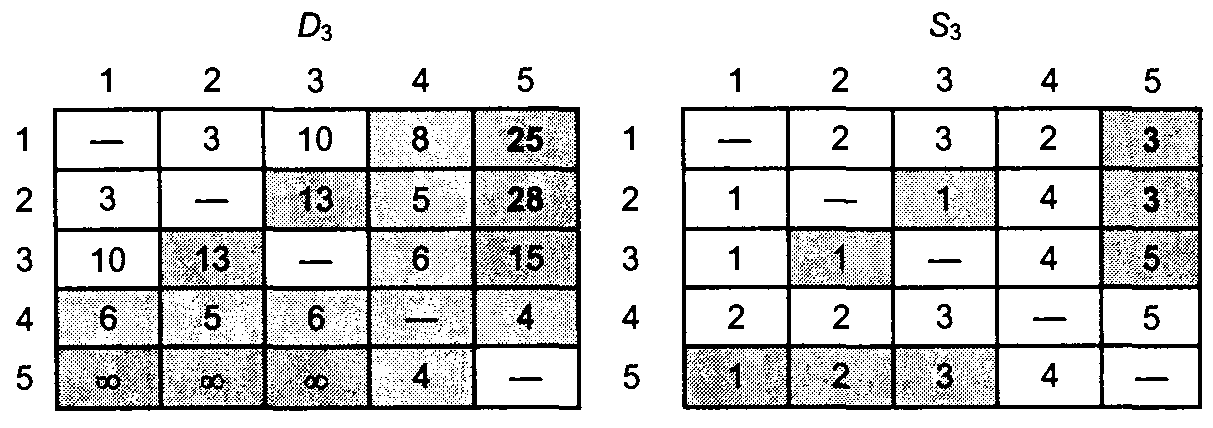
Этап 3. Полагаем k = 3; в матрице D2 выделены ведущие строка и столбец. Треугольный оператор применяется к затемненным элементам матриц D2 и S2. В результате получаем матрицы D3 и S3.
Этап 4. Полагаем k = 4, ведущие строка и столбец в матрице D3 выделены. Получаем новые матрицы D4 и S4
Этап 5. Полагаем k = 5, ведущие строка и столбец в матрице D4 выделены. Никаких действий на этом этапе не выполняем; вычисления закончены. Конечные матрицы D4 и S4 содержат всю информацию, необходимую для определения кратчайших путей между любыми двумя узлами сети. Например, кратчайшее расстояние между узлами 1 и 5 равно d15 = 12. Для определения соответствующих маршрутов напомним, что сегмент маршрута (i,j) состоит из ребра (i,j) только тогда, когда sij =j. В противном случае узлы i и j связаны, по крайней мере, через один промежуточный узел. Например, поскольку s15 = 4 и s45 = 5, сначала кратчайший маршрут между узлами 1 и 5 будет иметь вид 1 → 4 →5. Но так как s14 ≠4, узлы 1 и 4 в определяемом пути не связаны одним ребром (но в исходной сети они могут быть связаны непосредственно). Далее следует определить промежуточный узел (узлы) между первым и четвертым узлами. Имеем s14 = 2 и s24 = 4, поэтому маршрут 1 —> 4 заменяем 1 →2 → 4. Поскольку s12 = 2 и s24 = 4, других промежуточных узлов нет. Комбинируя определенные сегменты маршрута, окончательно получаем следующий кратчайший путь от узла 1 до узла 5:1→2→4→5. Длина этого пути равна 12 милям.
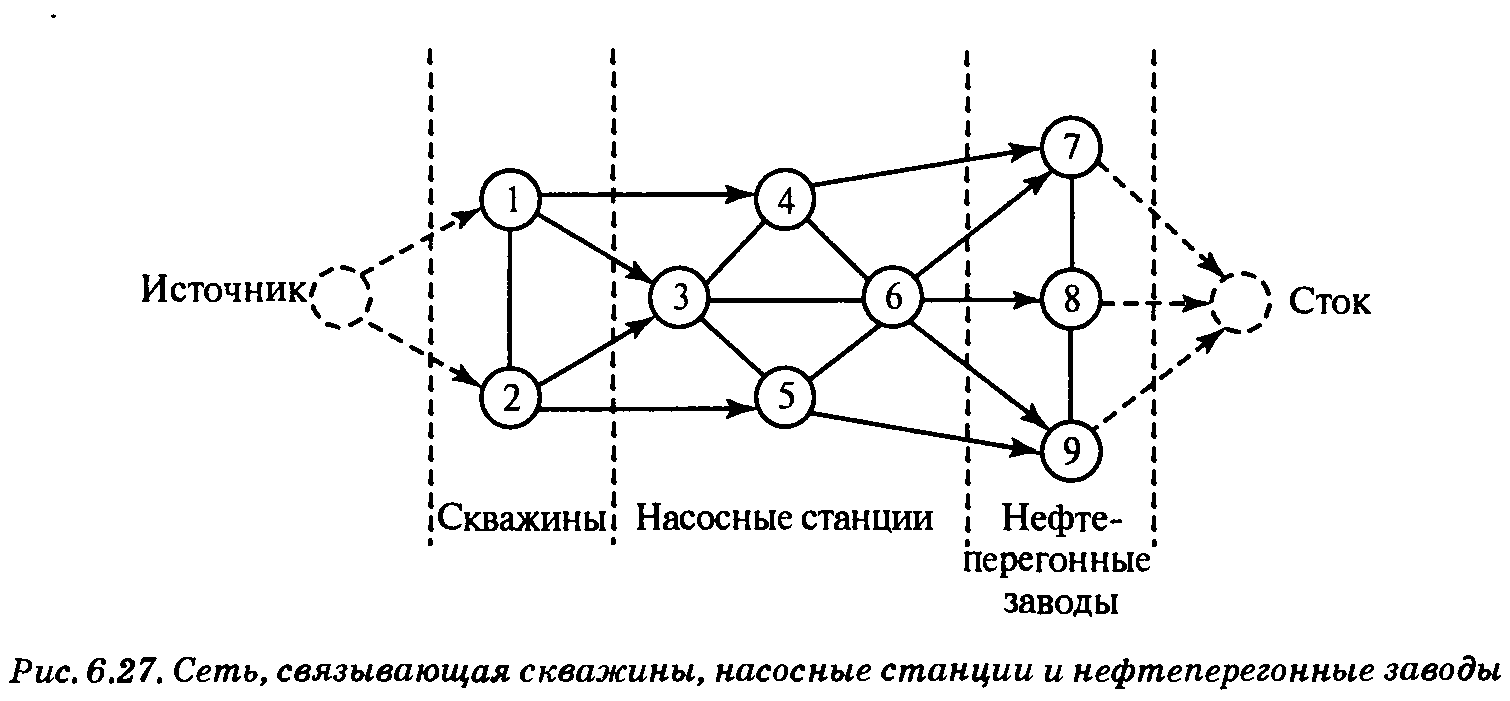
Тема 11. Задача о максимальном потоке Рассмотрим сеть трубопроводов для транспортировки сырой нефти от буровых скважин до нефтеперегонных заводов. Для перекачки нефти предусмотрены магистральные насосные станции. Каждый сегмент трубопровода имеет свою пропускную способность. Сегменты трубопровода могут быть как однонаправленные (осуществляют перекачку нефти только в одном направлении), так и двунаправленные. В однонаправленных сегментах положительная пропускная способность предполагается в одном направлении и нулевая — в другом. На рис. 6.27 показана типовая сеть нефтепроводов. Как определить максимальную пропускную способность (т.е. максимальный поток) между нефтяными скважинами и нефтеперегонными заводами? При решении данной задачи исходную сеть необходимо свести к сети с одним источником и одним стоком. Этого можно достичь, вводя дополнительные дуги с бесконечной пропускной способностью от источника к скважинам и от нефтеперегонных заводов к стоку (на рис. 6.27 эти дуги показаны пунктирными линиями). Для ребра (I,j), где i < j, используем запись (
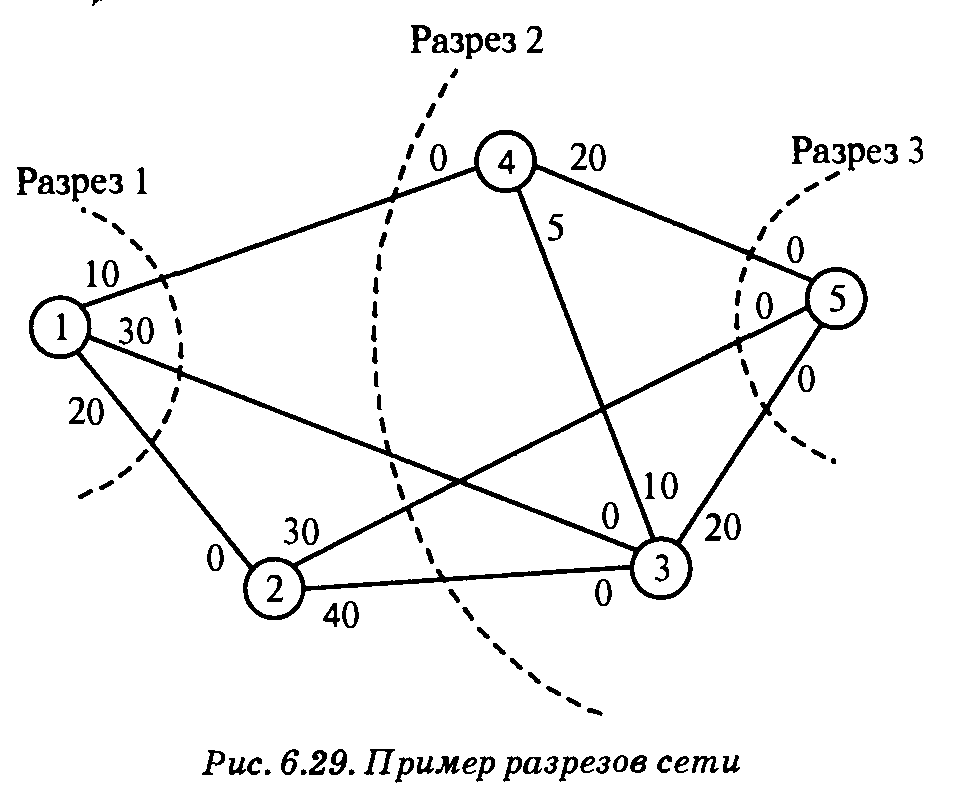
Перебор разрезов. Разрез определяет множество ребер, при удалении которых из сети полностью прекращается поток от источника к стоку. Пропускная способность разреза равна сумме пропускных способностей "разрезанных" ребер. Среди всех разрезов сети разрез с минимальной пропускной способностью определяет максимальный поток в сети. Пример: Рассмотрим сеть, показанную на рис. 6.29. На этом рисунке при обозначении пропускных способностей двунаправленных ребер придерживались соглашения, принятого ранее (рис. 6.28). Например, для ребра C, 4) пропускная способность в направлении 3 →4 равна 10, а в направлении 4 →3 — только 5.
Разрезы, представленные на рис. 6.29, имеют следующие пропускные способности. Вывод, который можно сделать на основе этих трех разрезов, заключается в том, что максимальный поток не может превышать 60 единиц. Но мы не можем сказать, каков максимальный поток на самом деле, так как не перебрали все возможные разрезы сети. К сожалению, перебор всех разрезов является непростой задачей. Поэтому для определения максимального потока в сети не используются алгоритмы, основанные на полном переборе разрезов. В следующем разделе будет показан эффективный алгоритм вычисления максимального потока.
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 782; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.84.179 (0.009 с.) |


 эквивалентна задаче максимизации величины
эквивалентна задаче максимизации величины  . Поскольку
. Поскольку  задача максимизации величины
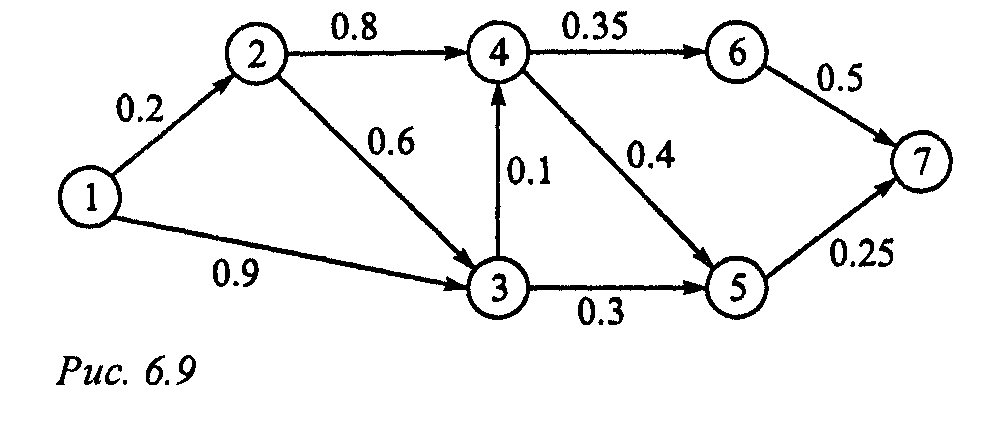
задача максимизации величины  . Заменив на рис. 6.10 вероятности
. Заменив на рис. 6.10 вероятности  на величины
на величины 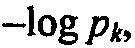 , получаем сеть (рис. 6.11), к которой можно применить алгоритм определения кратчайшего пути.
, получаем сеть (рис. 6.11), к которой можно применить алгоритм определения кратчайшего пути.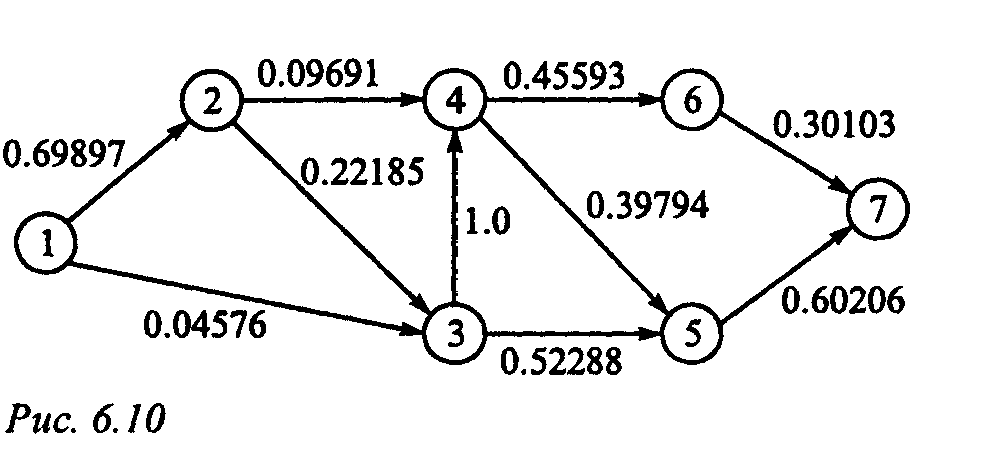


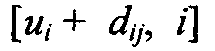 для всех узлов у, которые можно достичь непосредственно из узла i и которые не имеют постоянных меток. Если узел j уже имеет метку
для всех узлов у, которые можно достичь непосредственно из узла i и которые не имеют постоянных меток. Если узел j уже имеет метку 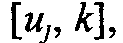 , полученную от другого узла k, и если
, полученную от другого узла k, и если  тогда метка
тогда метка 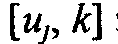 заменяется на
заменяется на 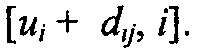
 с наименьшим значением расстояния
с наименьшим значением расстояния  среди всех временных меток (если таких меток несколько, то выбор произволен). Полагаем i = г и повторяем этап i.
среди всех временных меток (если таких меток несколько, то выбор произволен). Полагаем i = г и повторяем этап i.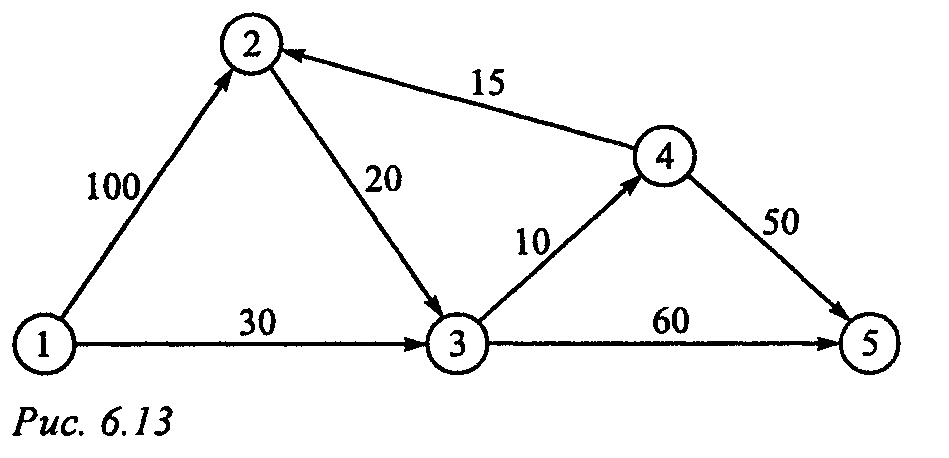

 . Поэтому статус метки этого узла изменяется на " постоянная".
. Поэтому статус метки этого узла изменяется на " постоянная".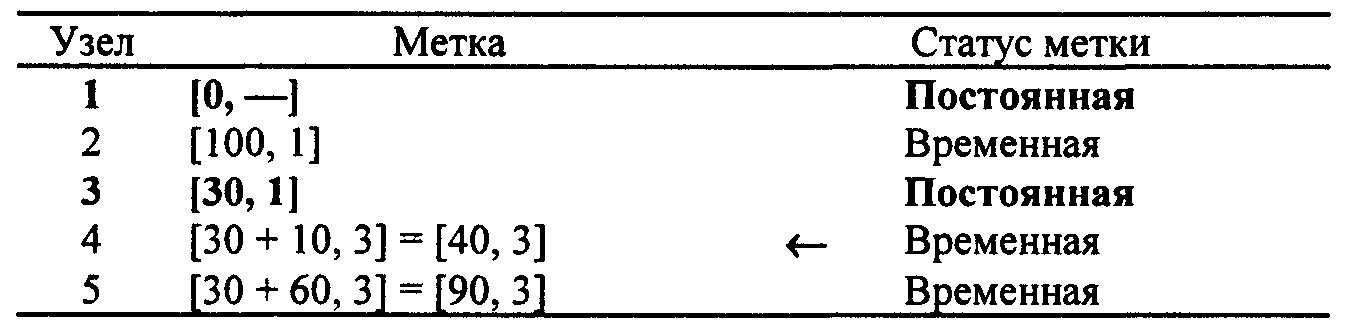
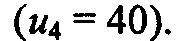
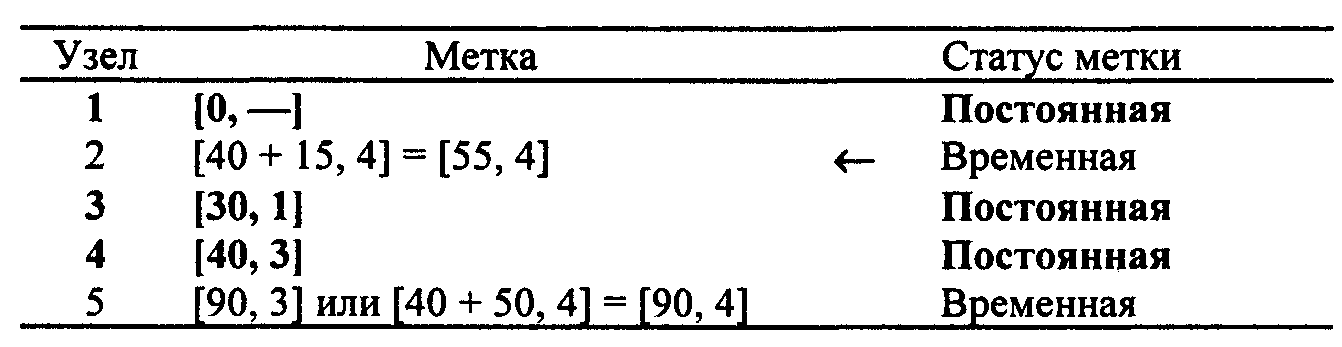


 , то целесообразно заменить путь i → k путем i →j→ k. Такая замена (далее ее будем условно называть треугольным оператором) выполняется систематически в процессе выполнения алгоритма Флойда.
, то целесообразно заменить путь i → k путем i →j→ k. Такая замена (далее ее будем условно называть треугольным оператором) выполняется систематически в процессе выполнения алгоритма Флойда.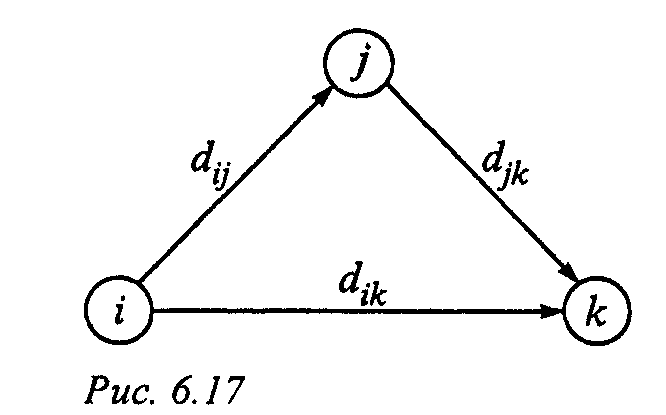

 (поскольку невозможен переход от узла 5 к узлу 3).
(поскольку невозможен переход от узла 5 к узлу 3).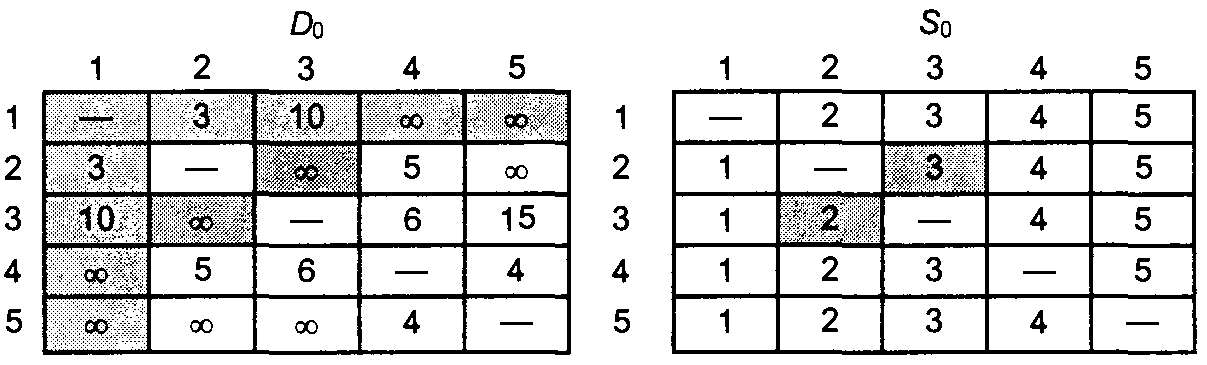

 .
. ,
, 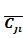 ) для представления пропускных способностей в направлениях i → j и j → i соответственно. Во избежание недоразумений на схеме сети
) для представления пропускных способностей в направлениях i → j и j → i соответственно. Во избежание недоразумений на схеме сети  -ближе к узлу у, как показано на рис. 6.28.
-ближе к узлу у, как показано на рис. 6.28.