
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Симплексный алгоритм для сетей с ограниченной пропускной способностью.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Предлагаемый алгоритм повторяет в точности те же этапы, что и обычный симплекс-метод. Вместе с тем здесь учитывается специальная структура сетевой модели. Строим симплексный алгоритм на основе условия Опишем алгоритм нахождения потока минимальной стоимости для сетей с ограниченной пропускной способностью. Отметим, что он базируется на стандартном симплекс-методе и теории двойственности. Шаг 0. Определяем для данной сети начальное базисное допустимое решение (множество дуг). Переходим к шагу 1. Шаг 1. С помощью условия оптимальности симплекс-метода определяем вводимую в базис переменную (дугу). Если на основе условия оптимальности определяем, что последнее решение оптимально, вычисления заканчиваются. В противном случае переходим к шагу 2. Шаг 2. На основе условия допустимости симплекс-метода определяем исключаемую из базиса переменную (дугу). Изменив базис, возвращаемся к шагу 1. Сети с n узлами и нулевым результирующим потоком (т.е. при выполнении равенства Вводимая переменная (дуга) на шаге 1 определяется путем вычисления разностей Обозначим через wi переменную задачи, двойственной к задаче ЛП, которая (переменная) соответствует ограничению узла i. Тогда данная двойственная задача формулируется следующим образом:
Из теории линейного программирования следует, что wi - wj = ci j для любой базисной дуги (i, j). Поскольку исходная задача ЛП по определению имеет одно избыточное ограничение, мы можем присвоить произвольное значение одной из переменных двойственной. Для определенности положим w1 = 0. Затем следует решить (базисную) систему уравнений wi - wj = ci j, чтобы вычислить остальные переменные двойственной задачи. Далее находим разности zij - cij для небазисных переменных согласно формуле
Теперь осталось показать, как определяется исключаемая из базиса переменная. Для этого рассмотрим следующий числовой пример. Пример: Сеть трубопроводов связывает две станции опреснения воды с двумя городами. Ежедневное предложение опреснительных станций составляет 40 и 50 миллионов галлонов воды, города ежедневно потребляют 30 и 60 миллионов галлонов воды. Каждая станция трубопроводами соединена с каждым городом непосредственно, однако они могут также перекачивать воду в города через специальную насосную станцию. Кроме того, станция 1 может транспортировать воду на станцию 2, а город 1 — в город 2. Данная сеть сбалансирована, так как в ней суммарный спрос равен суммарному предложению. Описанная сеть показана на рис. 6.43.
Итерация 0: Шаг 0. Определение начального допустимого базисного решения. Нетрудно построить остовное дерево (на рис. 6.44 показано сплошными дугами) для рассматриваемой сети. Отсюда получаем начальное допустимое базисное решение. Обычно, чтобы найти такое решение, используется метод введения искусственных переменных. На рис. 6.44 показано, что базисному решению соответствуют дуги (1, 3), (1, 4), (2, 3) и (3, 5) с потоками 30, 10, 50 и 60 единиц соответственно. Оставшиеся дуги (показаны пунктиром) представляют небазисные переменные. Запись х(с) показывает, что через соответствующую дугу с пропускной способностью с проходит поток х. По умолчанию считается, что х = 0 и с = ∞.
Итерация 1: Шаг 1. Определение вводимой в базис переменной. При решении системы уравнений
получим значения переменных двойственной задачи:
Теперь вычисляем разности
Таким образом, дуга (2, 5) будет введена в базисное решение. Шаг 2. Определение исключаемой из базиса переменной. На рис. 6.44 видно, что дуга (2, 5) совместно с базисными дугами (2, 3) и (3, 5) образует цикл. По определению остовное дерево не может содержать циклов. Поскольку поток через дугу (2, 5) должен возрасти, необходимо выровнять потоки через дуги, составляющие цикл таким образом, чтобы новое решение осталось допустимым. Для этого поток через дугу (2, 5) пометим знаком "+", потоки через другие дуги цикла — знаком "+" или "-", в зависимости от того, будут ли совпадать направления потоков в этих дугах с направлением потока в дуге (2, 5) при обходе цикла против часовой стрелки. Пометки дуг цикла показаны на рис. 6.44. При определении максимального потока, протекающего через дугу (2, 5), необходимо придерживаться следующих правил: 1. Новый поток в текущей базисной дуге не может быть отрицательным. 2. Поток через вводимую в базис дугу не может превышать ее пропускную способность. Применение правила 1 показывает, что потоки через дуги (2, 3) и (3, 5) нельзя уменьшить более, чем на min{50, 60} = 50 единиц. Из правила 2 следует, что поток через дугу (2, 5) не может превышать 30 единиц (пропускная способность этой дуги равна 30). Поэтому поток через дуги цикла изменится не более, чем на min{30, 50} = 30 единиц. Таким образом, поток через дугу (2, 5) равен 30 единиц, через дугу (2, 3) 50 - 30 = 20 единиц, а через дугу (3, 5) — 60 - 30 = 30 единиц. Поскольку ни какая из текущих базисных переменных не приняла нулевого значения, дуга (2, 5) должна остаться небазисной, но с ненулевым значением в 30 единиц. Чтобы выполнить требование равенства нулю небазисных переменных, сделаем подстановку
Эта подстановка изменит уравнения для потоков, протекающих через узлы 2 и 5. Текущее уравнение для потоков узла 2: Текущее уравнение для потоков узла 5: После подстановки Новое уравнение для потоков узла 2: Новое уравнение для потоков узла 5: Результаты этих изменений показаны на рис. 6.45. Направление потока через дугу (2, 5) изменилось на обратное (от узла 5 к узлу 2), причем, как и ожидалось, х52 = 0. Описанная подстановка также требует изменения стоимости прохождения потока по дуге (2, 5) до -1 долл. Те дуги, направления потоков которых изменены на противоположные, помечены в сети звездочкой.
Итерация 2. На рис. 6.45 представлены новые значения Величину потока через дугу (4, 5) можно увеличить до наименьшей из следующих величин. 1. Максимальный поток через дугу (4, 5), определяемый пропускной способностью, равен ∞. 2. Максимальное увеличение потока через дугу (1, 4) равно 35 - 30 = 5 единиц. 3. Максимальное уменьшение потока через дугу (1, 3) равно 10 единиц. 4. Максимальное уменьшение потока через дугу (3, 5) равно 30 единиц. Таким образом, поток через дугу (4, 5) можно увеличить до 5 единиц; эта дуга входит в базис, а дуга (1, 4) с потоком в 35 единиц исключается из базиса. Выполнив подстановку х14 = 35 – x41, получим сеть, показанную на рис. 6.46, где дуги (1, 3), (2, 3), (3, 5) и (4, 5) формируют остовное дерево сети (базисное решение). Для дуги (1, 4) с обратным направлением потока изменена стоимость прохождения потока до -5 долл. Проверьте самостоятельно, что в уравнения для потоков в узлах 1 и 4 будет добавлено 5 единиц входного потока.
Итерация 3. Вычисленные новые значения разностей
Итерация 4. Из новых значений разностей
Тема 13. Методы сетевого планирования На основе сетевых моделей разработано множество методов планирования, составления временных расписаний и управления проектами. Наиболее известные — метод критического пути (Critical Path Method — СРМ), а также система планирования и руководства программами разработок (Program Evaluation and Review Technique — PERT). В этих методах проекты рассматриваются как совокупность некоторых взаимосвязанных процессов (видов деятельности, этапов или фаз выполнения проекта), каждый из которых требует определенных временных и других ресурсов. В методах CPM и PERT проводится анализ проектов для составления временных графиков распределения фаз проектов. На рис. 6.50 в обобщенной форме показаны основные этапы реализации этих методов. На первом этапе определяются отдельные процессы, составляющие проект, их отношения последовательности (т.е. какой процесс должен предшествовать другому) и длительность. Далее проект представляется в виде сети, показывающей последовательность процессов, составляющих проект. На третьем этапе на основе построенной сети выполняются вычисления, в результате которых составляется временной график реализации проекта.
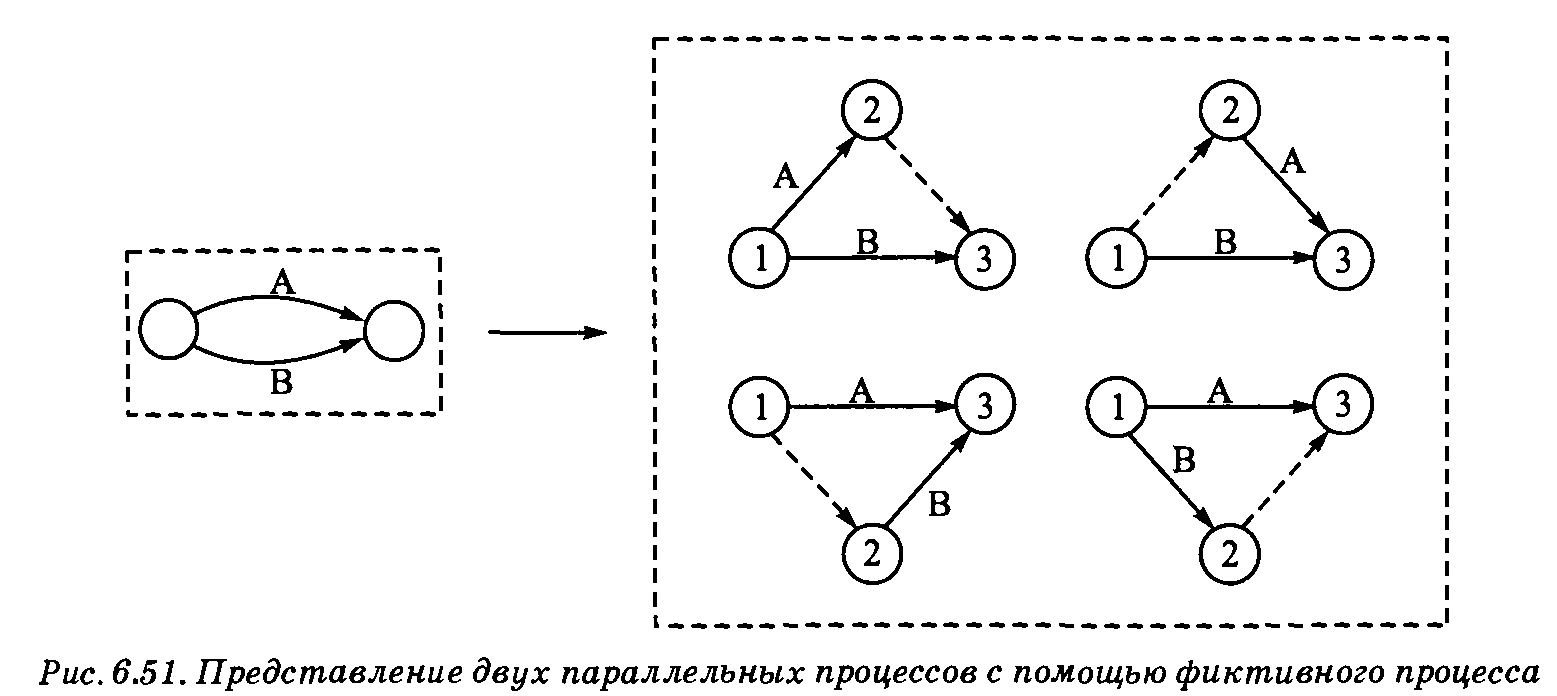
Методы СРМ и PERT, которые разрабатывались независимо друг от друга, отличаются тем, что в методе критического пути длительность каждого этапа проекта является детерминированной, тогда как в системе планирования PERT — стохастической. Рассмотрим сначала метод СРМ, а затем кратко PERT. Построение сети проекта. Каждый процесс проекта обозначается в сети дугой, ориентированной по направлению выполнения проекта. Узлы сети (также называемые событиями) устанавливают отношения предшествования среди процессов проекта. Построение сети проекта основано на следующих правилах. Правило 1. Каждый процесс в проекте представляется одной и только одной дугой. Правило 2. Каждый процесс идентифицируется двумя концевыми узлами. На рис. 6.51 показано, как с помощью фиктивного процесса можно представить два параллельных (конкурирующих) процесса А и В. По определению фиктивный процесс (который на схеме сети обычно обозначается пунктирной дугой) не поглощает временных или других ресурсов. Вставив фиктивный процесс одним из четырех способов, показанных на рис. 6.51, мы получаем возможность идентифицировать процессы А и В по крайней мере одним уникальным концевым узлом (как требует правило 2).
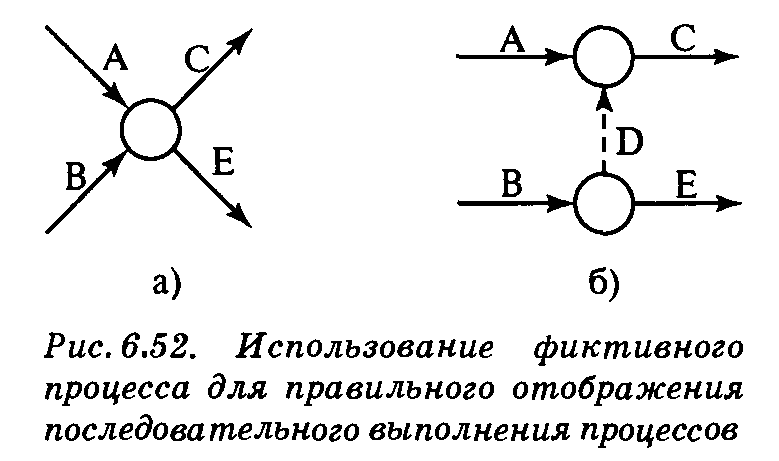
Правило 3. Для поддержания правильных отношений предшествования при включении в сеть любого процесса необходимо ответить на следующие вопросы. 1. Какой процесс непосредственно предшествует текущему? 2. Какой процесс должен выполняться после завершения текущего процесса? 3. Какой процесс конкурирует (выполняется параллельно) с текущим? Ответы на эти вопросы, возможно, потребуют включить в сеть фиктивные процессы, чтобы правильно отобразить последовательность выполнения процессов. Предположим, например, что четыре процесса должны удовлетворять следующим условиям.
1. Процесс С должен начаться сразу после завершения процессов А и В. 2. Процесс Е должен начаться непосредственно после завершения процесса В. На рис. (6.52, а) показано неправильное представление наших процессов, так как из него следует, что процесс Е должен начаться после завершения как процесса В, так и А. На рис. (6.52, б) показано, как с помощью фиктивного процесса D разрешить эту коллизию.
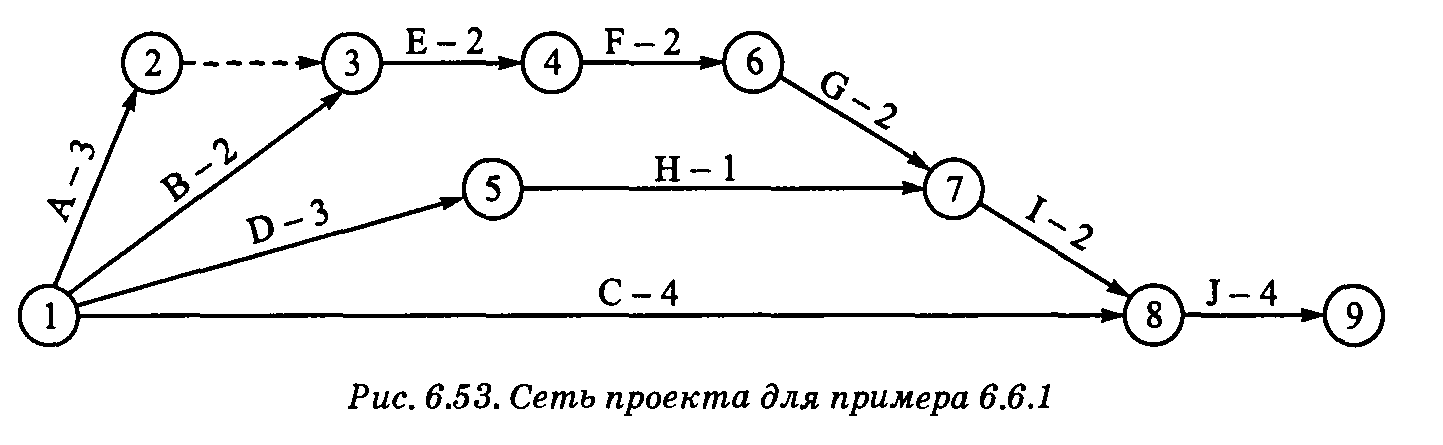
Пример: Издатель имеет контракт с автором на издание его книги. Ниже представлена последовательность (упрощенная) процессов, приводящая к реализации проекта издания книги. Необходимо разработать сеть для этого проекта.
На рис. 6.53 показана сеть, представляющая взаимосвязь процессов данного проекта. Фиктивный процесс (2, 3) введен для того, чтобы "развести" конкурирующие процессы А и В. Номера узлов сети возрастают в направлении выполнения проектов.
Метод критического пути. Конечным результатом применения метода критического пути (СРМ) будет построение временного графика выполнения проекта (см. рис. 6.50). Для этого проводятся специальные вычисления, в результате чего получаем следующую информацию. 1. Общая длительность выполнения проекта. 2. Разделение множества процессов, составляющих проект, на критические и некритические. Процесс является критическим, если он не имеет "зазора" для времени своего начала и завершения. Таким образом, чтобы весь проект завершился без задержек, необходимо, чтобы все критические процессы начинались и заканчивались в строго определенное время. Для некритического процесса возможен некоторый "дрейф" времени его начала, но в определенных границах, когда время его начала не влияет на длительность выполнения всего проекта. Для проведения необходимых вычислений определим событие как точку на временной оси, где завершается один процесс и начинается другой. В терминах сети, событие — это сетевой узел. Нам понадобятся также следующие определения и обозначения.
Вычисление критического пути включает два этапа (прохода). При проходе вперед вычисляются самые ранние времена наступления событий, а при проходе назад — самые поздние времена наступления тех же событий. · Проход вперед. Вычисления начинаются в узле 1 и заканчиваются в последнем узле n. Начальный шаг. Полагаем Основной шаг j. Для узла j определяем узлы р, q,..., v, непосредственно связанные с узлом j процессами (р, j), (q,j),..., (v,j), для которых уже вычислены самые ранние времена наступления соответствующих событий. Самое раннее время наступления события j вычисляется по формуле
Проход вперед завершается, когда будет вычислена величина · Проход назад. В этом проходе вычисления начинаются в последнем узле n и заканчиваются в узле 1. Начальный шаг. Полагаем Основной шаг j. Для узла у определяем узлы р, q,..., v, непосредственно связанные с узлом j процессами (j, p), (j, q),..., (j, v), для которых уже вычислены самые поздние времена наступления соответствующих событий. Самое позднее время наступления события j вычисляется по формуле
Проход назад завершается при вычислении величины Процесс (i, j) будет критическим, если выполняются три условия:
Если эти условия не выполняются, то процесс некритический. Критические процессы должны образовывать непрерывный путь через всю сеть от начального события до конечного. Пример: Найдем критический путь для сети проекта, показанной на рис. 6.54. Длительность всех процессов дана в днях.
Таким образом, расчеты показывают, что проект можно выполнить за 25 дней.
Вычисления без ошибок всегда приводят к результату Результаты вычислений, выполняемых при проходах вперед и назад, показаны рис. 6.54. Правила определения критических процессов показывают, что критический путь составляют процессы 1 —> 2 —> 4 —> 5 —> 6, т.е. этот путь проходит от начального узла 1 до конечного узла 6. Сумма длительностей критических процессов (1, 2), (2, 4), (4, 5) и (5, 6) равна длительности всего проекта (т.е. 25 дней). Отметим, что процесс (4, 6) удовлетворяет первым двум условиям критического пути
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 741; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.93.167 (0.014 с.) |

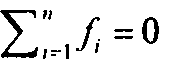 . Это условие означает, что в сети суммарный объем предложений равен суммарному объему спроса. Мы всегда можем удовлетворить данное условие, введя фиктивный источник или сток, которые можно связать с остальными узлами сети дугами с нулевой стоимостью и бесконечной пропускной способностью. Однако сбалансированность сети не гарантирует существования допустимого решения, поскольку этому может воспрепятствовать ограниченность пропускных способностей дуг.
. Это условие означает, что в сети суммарный объем предложений равен суммарному объему спроса. Мы всегда можем удовлетворить данное условие, введя фиктивный источник или сток, которые можно связать с остальными узлами сети дугами с нулевой стоимостью и бесконечной пропускной способностью. Однако сбалансированность сети не гарантирует существования допустимого решения, поскольку этому может воспрепятствовать ограниченность пропускных способностей дуг. ) соответствуют n- 1 независимым ограничениям в виде равенств. Поэтому базисное решение должно содержать n - 1 переменных. Можно показать, что базисное решение соответствует остовному дереву данной сети.
) соответствуют n- 1 независимым ограничениям в виде равенств. Поэтому базисное решение должно содержать n - 1 переменных. Можно показать, что базисное решение соответствует остовному дереву данной сети. для всех текущих небазисных дуг (i, j). Если для всех разностей
для всех текущих небазисных дуг (i, j). Если для всех разностей  тогда текущее базисное решение оптимально. Иначе в качестве вводимой в базис переменной выбираем дугу, которой соответствует наибольшее положительное значение разности
тогда текущее базисное решение оптимально. Иначе в качестве вводимой в базис переменной выбираем дугу, которой соответствует наибольшее положительное значение разности 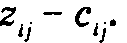

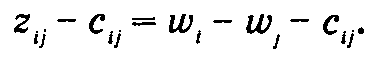




 для небазисных переменных.
для небазисных переменных.
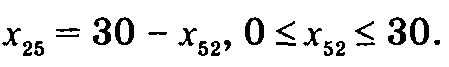
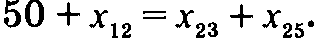
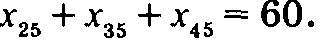
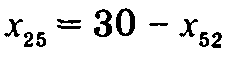 получим следующее.
получим следующее.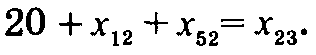
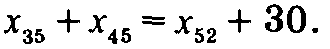

 . Очевидно, что в базис следует ввести дугу (4, 5). Введение в базис этой дуги также приводит к образованию цикла.
. Очевидно, что в базис следует ввести дугу (4, 5). Введение в базис этой дуги также приводит к образованию цикла.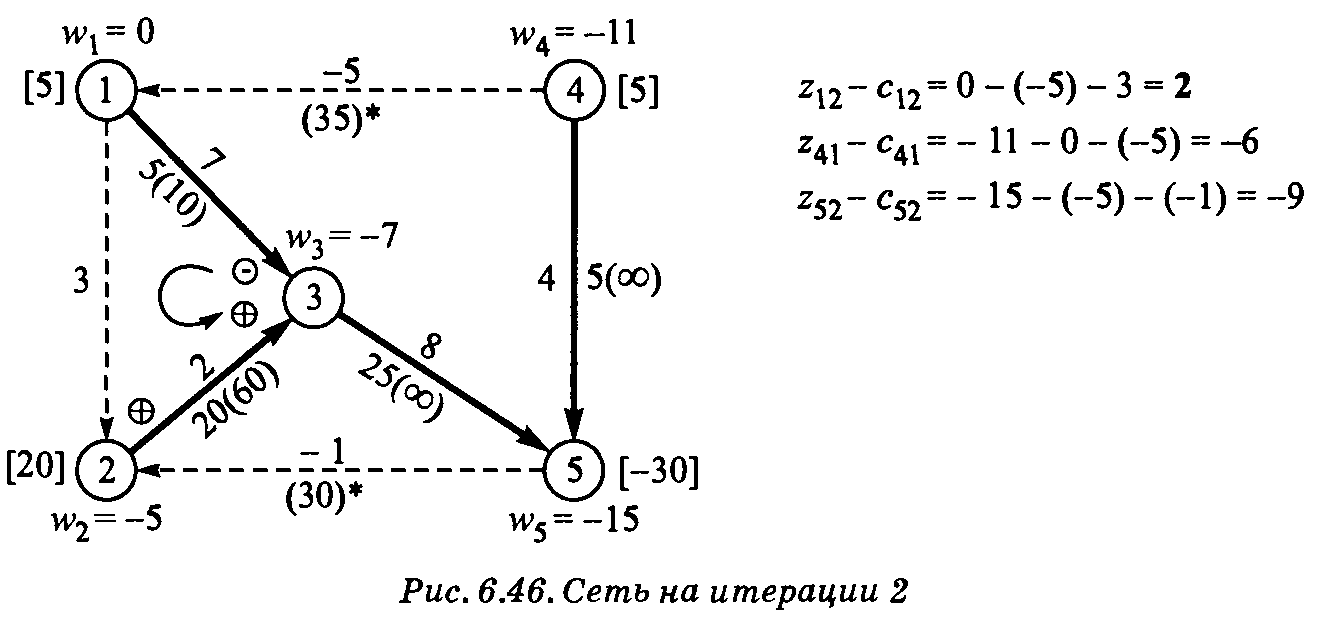
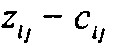 для небазисных дуг (1, 2), (4, 1) и (5, 2) показаны на рис. 6.46. Из этих значений вытекает, что в базис следует ввести дугу (1, 2) с потоком в 5 единиц, тогда как дуга (1, 3) исключается из базиса с нулевым значением потока. Новое решение представлено на рис. 6.47.
для небазисных дуг (1, 2), (4, 1) и (5, 2) показаны на рис. 6.46. Из этих значений вытекает, что в базис следует ввести дугу (1, 2) с потоком в 5 единиц, тогда как дуга (1, 3) исключается из базиса с нулевым значением потока. Новое решение представлено на рис. 6.47.
 (рис. 6.47) видно, что последнее решение оптимально. Значения исходных переменных получаем путем обратной подстановки, как показано на рис. 6.47.
(рис. 6.47) видно, что последнее решение оптимально. Значения исходных переменных получаем путем обратной подстановки, как показано на рис. 6.47.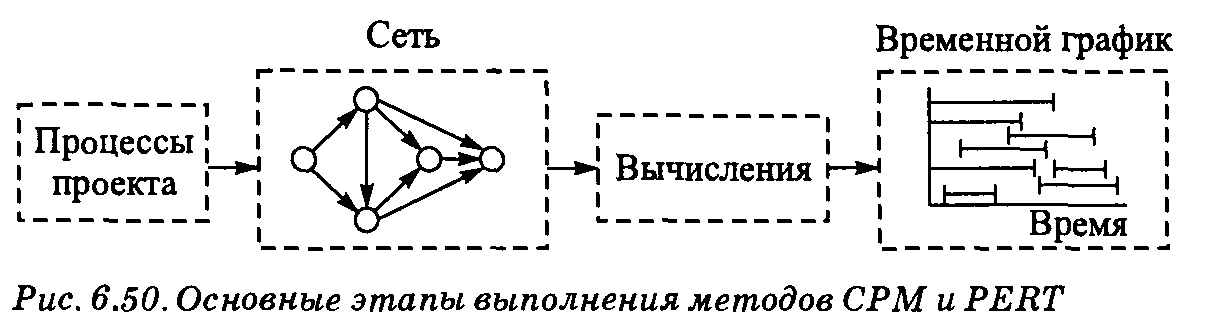


 это указывает на то, что проект начинается в нулевой момент времени.
это указывает на то, что проект начинается в нулевой момент времени.
 для узла n. По определению величина
для узла n. По определению величина  равна самому длинному пути (длительности) от начала проекта до узла (события) j.
равна самому длинному пути (длительности) от начала проекта до узла (события) j. это указывает, что самое раннее и самое позднее времена для завершения проекта совпадают.
это указывает, что самое раннее и самое позднее времена для завершения проекта совпадают.
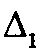 , для узла 1.
, для узла 1.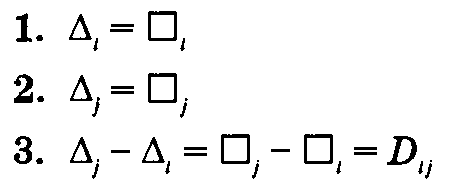


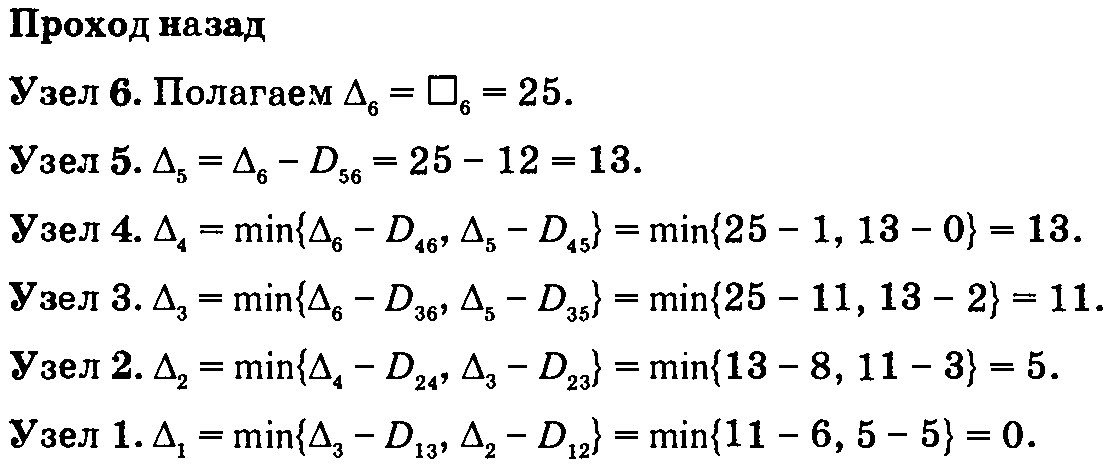
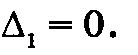
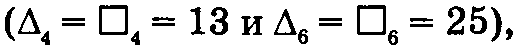 но не удовлетворяет третьему условию
но не удовлетворяет третьему условию  Поэтому данный процесс не является критическим.
Поэтому данный процесс не является критическим.


