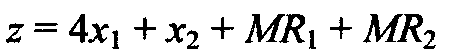Искусственное начальное решение.

Часто при начальном допустимом базисном решении гарантировалось, что все последующие базисные решения, получаемые при выполнении симплекс-метода, также будут допустимыми. В задачах линейного программирования, где все ограничения являются неравенствами типа "≤" (с неотрицательной правой частью), дополнительные (остаточные) переменные позволяют сформировать начальное допустимое базисное решение. Естественно, возникает вопрос: как найти начальное допустимое базисное решение в задачах ЛП, где есть ограничения в виде

равенств или неравенств типа "≥"?

Наиболее общим способом построения начального допустимого базисного решения задачи ЛП является использование искусственных переменных. Эти переменные в первой итерации играют роль дополнительных остаточных переменных, но на последующих итерациях от них освобождаются. Разработано два тесно связанных между собой метода нахождения начального решения, которые используют искусственные переменные:

· М-метод

· Двухэтапный метод.

М-метод.

Пусть задача ЛП записана в стандартной форме. Для любого равенства i, в котором не содержится дополнительная остаточная переменная, введем искусственную переменную R_i, которая далее войдет в начальное базисное решение. Но, поскольку эта переменная искусственна (другими словами, не имеет никакого "физического смысла" в данной задаче), необходимо сделать так, чтобы на последующих итерациях она обратилась в нуль. Для этого в выражение целевой функции вводят штраф.

Переменная R_i, с помощью достаточно большого положительного числа М штрафуется путем ввода в целевую функцию выражения -MR_i в случае максимизации целевой функции и выражения +MR_i, — в случае минимизации. Вследствие этого штрафа естественно предположить, что процесс оптимизации симплекс-метода приведет к нулевому значению переменной R_i. Следующий пример проясняет детали этого метода.

Пример.

Минимизировать

При выполнении условий

Стандартная форма этой задачи получается в результате добавления дополнительной (избыточной) переменной х₃ во второе неравенство и дополнительной (остаточной) переменной х₄ в третье неравенство. Эта задача в стандартной форме будет записана следующим образом:

Минимизировать z = 4x₁ + х₂

При выполнении условий

В полученной задаче первое и второе уравнения не имеют дополнительных (остаточных) переменных, которые можно ввести в базисное решение. Поэтому введем в эти уравнения искусственные переменные R₁ и R₂, а в целевую функцию добавим штраф MR_l + MR₂. В результате получим следующую задачу ЛП.

Минимизировать

При выполнении условий

В этой модифицированной задаче переменные R₁ и R₂ и х₄ можно использовать в качестве начального допустимого базисного решения. В результате получим следующую симплекс-таблицу.

Прежде чем применять симплекс-метод, надо согласовать значения в z-строке с остальной частью таблицы. В частности, значение функции z, соответствующее начальному базисному решению R₁ = 3, R₂ = 6 и х₄ = 4, должно равняться ЗМ+ 6М + 0 = 9M, а не 0, как показано в таблице. Это противоречие связано с тем, что переменным R₁ и R₂ соответствуют ненулевые коэффициенты (-М, -М) в строке z. Чтобы сделать эти коэффициенты нулевыми, следует умножить элементы строк R₁ и R₂ на величину М, и затем сложить эти строки с z-строкой. (Обратите внимание на "подсвеченные" единицы в этих строках — если бы эти коэффициенты были отличны от единиц, то необходимо было бы сначала разделить все элементы этих строк на данные коэффициенты). Кратко это действие можно записать следующим образом.

Новая z-строка = старая z-строка + М х R_1-строка + М х R₂-строка

Измененная симплекс-таблица примет следующий вид:

Отметим, что теперь z = 9М, что соответствует базисному решению R₁ = 3, R₂ = 6 и

x₄ =4.

Последняя таблица готова к применению симплекс-метода с использованием условий оптимальности и допустимости. Поскольку мы минимизируем целевую функцию, находим наибольший положительный коэффициент в z-строке. Наибольший коэффициент -4 + 7М соответствует переменной x_1, которая и будет вводимой. Условие допустимости указывает на переменную R₁ в качестве исключаемой.

Поскольку вводимая и исключаемая переменные определены, новую симплекс- таблицу можно вычислить с помощью метода Гаусса-Жордана. Заметим, что вычисления в z-строке, где присутствует М, следует проводить алгебраически. Так, для получения новой z-строки надо новую ведущую строку умножить на -(-4 + 7М) и сложить с текущей z-строкой. В результате получим следующую таблицу:

Отметим, что уже первая итерация исключила из базисного решения искусственную переменную R₁, что является результатом включения штрафа в целевую функцию.

Последняя таблица показывает, что следующими (вводимой и исключаемой) переменными будут х₂ и R₂ соответственно. Конечно, для получения оптимального решения может потребоваться больше двух итераций. В данной задаче оптимальным решением будет х₁ = 2/5, х₂ = 9/5, х₃ = 1 и z = 17/5.

При использовании М-метода следует обратить внимание на следующие два обстоятельства:

1. Использование штрафа М может и не привести к исключению искусственной переменной в конечной симплекс-итерации. Если исходная задача линейного программирования не имеет допустимого решения (например, система ограничений несовместна), тогда в конечной симплекс-итерации по крайней мере одна искусственная переменная будет иметь положительное значение. Это "индикатор" того, что задача не имеет допустимого решения.

2. Теоретически применение М-метода требует, чтобы М —> °°. Однако с точки зрения компьютерных вычислений величина М должна быть конечной и, вместе с тем, достаточно большой. Как понимать термин "достаточно большая" — это открытый вопрос. Величина М должна быть настолько большой, чтобы выполнять роль "штрафа", но не слишком большой, чтобы не уменьшить точность вычислений. На практике вы должны помнить о возможных