
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ошибках машинного округления при выполнении вычислений, в которых совместно участвуют как большие, так и малые числа.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Двухэтапный метод. Двухэтапный метод лишен недостатков, которые присущи М-методу вследствие ошибок округления. Как следует из названия этого метода, процесс решения задачи ЛП разбивается на два этапа. На первом этапе ведется поиск начального допустимого базисного решения. Если такое решение найдено, то на втором этапе решается исходная задача. Этап 1. Задача ЛП записывается в стандартной форме, а в ограничения добавляются необходимые искусственные переменные (как и в М-методе) для получения начального базисного решения. Решается задача ЛП минимизации суммы искусственных переменных с исходными ограничениями. Если минимальное значение этой новой целевой функции больше нуля, значит, исходная задача не имеет допустимого решения, и процесс вычислений заканчивается. (Напомним, что положительные значения искусственных переменных указывают на то, что исходная система ограничений несовместна.) Если новая целевая функция равна нулю, переходим ко второму этапу. Этап 2. Оптимальное базисное решение, полученное на первом этапе, используется как начальное допустимое базисное решение исходной задачи. Пример: Этап 1. Минимизировать При ограничениях
Соответствующая таблица имеет вид:
Как и в М - методе, сначала вычисляется новая r-строка по формуле новая r-строка = старая r-строка + 1 х R1-строка + 1 х R2-строка Новая r-строка используется для решения задачи первого этапа, что приведет к следующему оптимальному решению:
Поскольку достигнут минимум г = 0, значит, на первом этапе получено допустимое базисное решение x1 = 3/5, х2 = 6/5 и x4 = 1. Искусственные переменные полностью выполнили свою "миссию", поэтому из последней таблицы можно удалить их столбцы. Переходим ко второму этапу. Этап 2 После удаления искусственных переменных исходная задача будет записана следующим образом. Минимизировать При ограичениях
Обратите внимание на то, что после первого этапа исходная задача претерпела некоторые изменения, которые учитывают полученное базисное решение. Этой трансформированной задаче соответствует следующая таблица.
Поскольку базисные х1 и х2 имеют ненулевые коэффициенты в z-строке, эту строку следует преобразовать.
Начальная таблица второго этапа примет следующий вид.
Так как решается задача минимизации, следует ввести переменную х3 в базис. Применение алгоритма симплекс-метода уже на следующей итерации приведет к оптимальному решению. Удаление искусственных переменных в конце первого этапа имеет смысл только тогда, когда все они являются небазисными. Однако возможна ситуация, когда в конце первого этапа искусственные переменные останутся в базисе, но будут иметь нулевые значения. В этом случае такие переменные необходимости будут формировать часть начального базисного решения для второго этапа. При этом необходимо так изменить вычисления, выполняемые на втором этапе, чтобы искусственные переменные никогда не смогли принять положительные значения ни в каких итерациях симплекс-метода. Существует простое правило, которое гарантирует, что нулевая базисная искусственная переменная на втором этапе никогда не станет положительной. 1. Если в ведущем столбце коэффициент, соответствующий нулевой базисной искусственной переменной, положителен, тогда ведущий элемент определяется автоматически (поскольку ему соответствует минимальное отношение, равное нулю), и искусственная переменная на следующей итерации становится небазисной. 2. Если ведущий элемент равен нулю, следующая итерация оставляет искусственную переменную нулевой. 3. Если ведущий элемент отрицательный, то минимальное отношение не ассоциируется с базисной (нулевой) искусственной переменной. В этом случае, если минимальное отношение будет положительным, то на следующей итерации искусственная переменная примет положительное значение. Чтобы исключить эту возможность, мы принуждаем искусственную переменную всегда оставаться в базисном решении. Поскольку искусственная переменная равна нулю, ее удаление из базисного решения не влияет на то, будет ли допустимым решение из оставшихся в базисе переменных. Итак, правило для второго этапа заключается в том, чтобы искусственные переменные оставлять в базисе всегда, когда коэффициент в ведущем столбце положителен или отрицателен. Фактически это правило применяется в конце первого этапа, когда из базисного решения удаляются нулевые искусственные переменные, перед тем как приступить ко второму этапу.
Модуль 2. Двойственность и анализ чувствительности. Сетевые модели (18 часов) Тема 6. Определение двойственной задачи. Каждой задаче линейного программирования можно определенным образом сопоставить некоторую другую задачу (линейного программирования), называемую двойственной или сопряженной по отношению к исходной или прямой задаче. Дадим определение двойственной задачи по отношению к общей задаче линейного программирования, состоящей, как мы уже знаем, в нахождении максимального значения функции
при условиях
Определение 1. Задача, состоящая в нахождении минимального значения функции
при условиях
называется двойственной по отношению к задаче (32) – (34). Задачи (32) – (34) и (35) – (37) образуют пару задач, называемую в линейном программировании двойственной парой. Сравнивая две сформулированные задачи, видим, что двойственная задача составляется согласно следующим правилам: 1. Целевая функция исходной задачи (32) – (34) задается на максимум, а целевая функция двойственной (35) – (37) – на минимум. 2. Матрица
составленная из коэффициентов при неизвестных в системе ограничений (33) исходной задачи (32) – (34), и аналогичная матрица
в двойственной задаче (35) – (37) получаются друг из друга транспонированием (т. е. заменой строк столбцами, а столбцов – строками). 3. Число переменных в двойственной задаче (35) – (37) равно числу ограничений в системе (33) исходной задачи (32) – (34), а число ограничений в системе (36) двойственной задачи – числу переменных в исходной задаче. 4. Коэффициентами при неизвестных в целевой функции (35) двойственной задачи (35) – (37) являются свободные члены в системе (33) исходной задачи (32) – (34), а правыми частями в соотношениях системы (36) двойственной задачи – коэффициенты при неизвестных в целевой функции (32) исходной задачи. 5. Если переменная xj исходной задачи (32) – (34) может принимать только лишь положительные значения, то j –е условие в системе (36) двойственной задачи (35) – (37) является неравенством вида “? ”. Если же переменная xj может принимать как положительные, так и отрицательные значения, то 1 – соотношение в системе (54) представляет собой уравнение. Аналогичные связи имеют место между ограничениями (33) исходной задачи (32) – (34) и переменными двойственной задачи (35) – (37). Если i – соотношение в системе (33) исходной задачи является неравенством, то i –я переменная двойственной задачи Двойственные пары задач обычно подразделяют на симметричные и несимметричные. В симметричной паре двойственных задач ограничения (33) прямой задачи и соотношения (36) двойственной задачи являются неравенствами вида “ Пример 1. Составить двойственную задачу по отношению к задаче, состоящей в максимизации функции
при условиях
Решение. Для данной задачи
Число переменных в двойственной задаче равно числу уравнений в системе (41), т. е. равно трем. Коэффициентами в целевой функции двойственной задачи являются свободные члены системы уравнений (41), т.е. числа 12, 24, 18. Целевая функция исходной задачи (40) – (42) исследуется на максимум, а система условий (41) содержит только уравнения. Поэтому в двойственной задаче целевая функция исследуется на минимум, а ее переменные могут принимать любые значения (в том числе и отрицательные). Так как все три переменные исходной задачи (40) – (42) принимают только лишь неотрицательные значения, то в системе условий двойственной задачи должны быть три неравенства вида “? ”. Следовательно, для задачи (40) – (42) двойственная задача такова: найти минимум функции
Пример 2. Для задачи, состоящей в максимизации функции
при условиях
сформулировать двойственную задачу. Решение. Для данной задачи
В соответствии с общими правилами задача, двойственная по отношению к данной, формулируется следующим образом: найти минимум функции
|
|||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 452; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.91.78 (0.013 с.) |








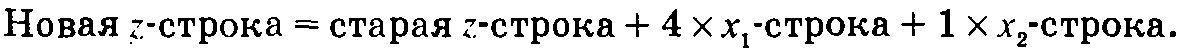

 (32)
(32) (33)
(33)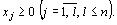 (34)
(34)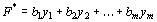 (35)
(35) (36)
(36) (37)
(37) (38)
(38) (39)
(39) . В противном случае переменная уj может принимать как положительные, так и отрицательные значения.
. В противном случае переменная уj может принимать как положительные, так и отрицательные значения. ”. Таким образом, переменные обеих задач могут принимать только лишь неотрицательные значения.
”. Таким образом, переменные обеих задач могут принимать только лишь неотрицательные значения. (40)
(40) (41)
(41)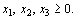 (42)
(42) и
и 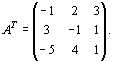
 при условиях
при условиях



 ,
, 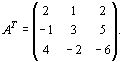
 при условиях
при условиях



