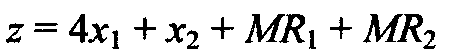Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математические модели исследования операций.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Методы исследования операций. Методология Исследования операций зависит от характера данных, являющихся предметом изучения. 1. Статистические методы. Данные, на которые опирается исследование, добываются в большинстве случаев посредством статистического изучения операций. Однако данные по ранее проведенным операциям не равноценны данным эксперимента, так как обычные операции протекают вне научного контроля. Данные носят случайный характер наблюдений, а не систематического экспериментирования; при этом примитивные методы подсчета могут привести к серьезным ошибкам. Таким образом, статистический анализ применим только в том случае, над операцией произведено большое число однородных по характеру наблюдений. 2. Сбор данных. Помимо сбораданных важной задачей при их сборе является проверка полноты полученных данных. 3. Ограниченность данных. Наблюдения при исследовании операций носят статистический характер. Поскольку операцией нельзя полностью управлять как научным экспериментом, суждение о причинах успеха или неуспеха часто может быть вынесено только на основании сравнения большого числа одинаковых операций и нахождения статистическими методами результата изменения той или иной черты обстановки. Это накладывает некоторое ограничение на полезность статистического исследования, поскольку пределы естественных вариаций обстановки обычно невелики. 4. Индивидуальные суждения. Сведения, представленные несколькими десятками участников операции, носят весьма сомнительный характер, так как участники редко правильно оценивают случайные события. Всегда следует иметь в виду необходимость непредвзятого и неограниченного знания фактов, а не мнений или суждений. 5. Опытные операции. Для исследования операций может применяться экспериментальный метод. Можно в операции намеренно изменять выбранные условия, а затем управлять ими. Для этой цели чаще всего применяются маневры, организованные так, чтобы можно было получить количественные данные о действиях в ходе операции. 6. Аналитические методы. Исследование операций могут также включать теоритические, отвлеченные методы исследования. Теоритическое построение любой науки всегда начинается с изучения до предела упрощенных частных случаев. Только после окончания этой части работы и проверки ее практикой можно вводить последующие усложнения и изучать случаи, имеющие большой практический интерес.
7. Обзор методов. Сначала собираются данные о прошедших операциях. Отклонения в результатах операции сопоставляются с отклонениями в условиях проведения операции – параметрами операции – для нахождения между ними зависимостей. Далее применяются различные меры оценки эффективности операции, чтобы выбрать ту из них, которая наиболее точно отражает зависимость исхода операции от условий ее проведения. Далее исследование сосредотачивается на тех параметрах операции, которые наиболее сильно влияют на ее исход с точки зрения принятого критерия оценки. Исследование операции будет считаться законченным, когда будет получена ясная зависимость исхода операции от изменения различных ее условий – параметров операции. 8. Общие замечания. Существенным отличием условий работы по исследованию операций от других видов научной работы является обстановка неотложности. Имитационное моделирование. Альтернативой математическому моделированию сложных систем может служить имитационное моделирование. Этот вид моделирования часто является наилучшим (если не единственным) способом исследования реальных систем. Различие между «входом» и «выходом» может быть явно не задано. Вычисленные аспекты имитационных моделей обычно сравнительно несложные, но, как правило, очень трудоемкие. Поэтому реализация некоторых имитационных моделей даже на современных быстрых и высокопроизводительных компьютерах может быть очень медленной. Процесс получения решения для задачи исследования операций с использованием компьютера включает несколько этапов: Этап 1. Ставятся цели и задачи исследования, проводится качественное описание объекта. Этап 2. Формируется математическая модель изучаемого объекта, которая включает три основных элемента: 1. Переменные, которые следует определить. 2. Целевую функцию, подлежащую оптимизации 3. Ограничения, которым должны удовлетворять переменные. Этап 3. Осуществляется выбор (или разработка) методов исследования.
Этап 4. Проводится программирование (реализация) модели на компьютере; подготавливается исходная информация для проверки правильности модели. Этап 5. Проводится проверка модели на основе анализа полученных результатов моделирования. Результаты такой работы нередко приводят к перестройке модели и, соответственно, к составлению новых программ. Искусство моделирования. В связи с развитием техники, ростом промышленного производства и с появлением ЭВМ все большую роль начали играть задачи отыскания оптимальных решений в различных сферах человеческой деятельности. Основным инструментом при решении этих задач стало математическое моделирование - формальное описание изучаемого явления и исследование с помощью математического аппарата. Искусство математического моделирования состоит в том, чтобы учесть как можно больше факторов по возможности простыми средствами. Именно в силу этого процесс моделирования часто носит итеративный характер. На первой стадии строится относительно простая модель и проводится ее исследование, позволяющее понять, какие из существенных свойств изучаемого объекта не улавливаются данной формальной схемой. Затем происходит уточнение, усложнение модели. В большинстве случаев первой степенью приближения к реальности является модель, в которой все зависимости между переменными, характеризующими состояние объекта, предполагаются линейными. Здесь имеется полная аналогия с тем, как весьма важная и зачастую исчерпывающая информация о поведении произвольной функции получается на основе изучения ее производной, происходит замена этой функции в окрестности каждой точки линейной зависимостью. Значительное количество экономических, технических и других процессов достаточно хорошо и полно описывается линейными моделями.
Тема 2. Введение в линейное программирование Таблица 1
Отдел маркетинга компании ограничил ежедневное производство краски для внутренних работ до 2 т. (из-за отсутствия надлежащего спроса), а также поставил условие, чтобы ежедневное производство краски для внутренних работ не превышало больше, чем на тонну аналогичный показатель производства краски для внешних работ. Компания хочет определить оптимальное (наилучшее) соотношение между видами выпускаемой продукции общего ежедневного дохода. Задача линейного программирования, как и любая задача исследования операций, включает три основных элемента 1) Переменные, которые следует определить, 2) Целевую функцию, подлежащую оптимизации, 3) Ограничения, которым должны удовлетворять переменные. Переменные задачи: x1- план выпуска краски для наружных работ, x2- план выпуска краски для внутренних работ. Целевая функция: Величина общей прибыли Z=5*x1+4*x2 Ограничения: 6*x1+4*x2<=24 x1+2*x2<=6 х2 – х1<=1 x2<=2 x1,x2>=0. Нахождение минимума целевой функции. Стоимость ресурсов. Во многих моделях линейного программирования ограничения трактуются как условия ограниченности ресурсов. В таких ограничениях правая часть неравенств является верхней границей количества доступных ресурсов. Рассмотрим чувствительность оптимального решения к изменению ограничений, накладываемых на ресурсы.
Такой анализ задачи ЛП предлагает простую меру чувствительности решения, называемую стоимостью единицы ресурса; при изменении количества доступных ресурсов (на единицу) значение целевой функции в оптимальном решении изменится на стоимость единицы ресурса. Проиллюстрируем этот вид анализа задачи ЛП на следующем примере.
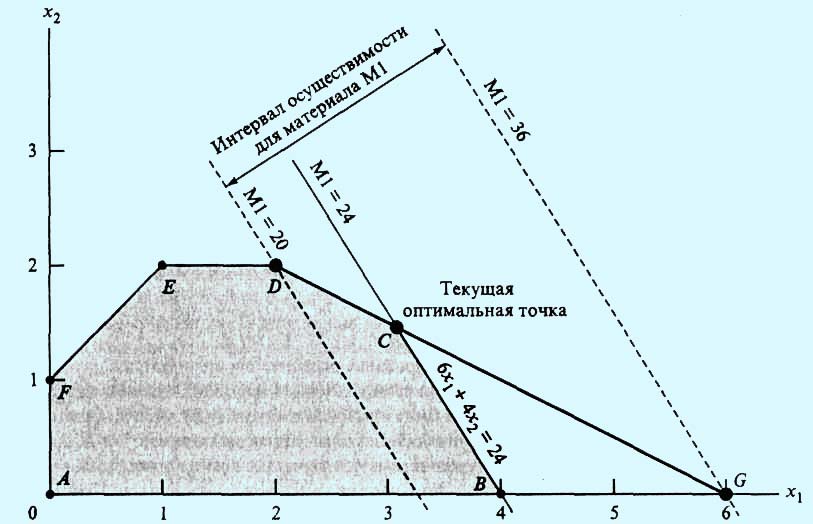
Пример 1. В модели для компании "Русские краски" первые два неравенства представляют собой ограничения на использование сырья M1 и М2 соответственно. Определим стоимость единиц этих ресурсов. Начнем с ограничения для сырья M1. Напомним, что в данной задаче оптимальное решение достигается в угловой точке С, являющейся точкой пересечения прямых, соответствующих ограничениям на сырье M1 и М2 (рис. 1).
При изменении уровня доступности материала M1 (увеличение или уменьшение текущего уровня, равного 24 т) точка С оптимального решения "плывет" вдоль отрезка DG. Любое изменение уровня доступности материала M1, приводящее к выходу точки пересечения С из этого отрезка, ведет к неосуществимости оптимального решения в точке С. Поэтому можно сказать, что концевые точки D = (2, 2) и G = (6, 0) отрезка DG определяют интервал осуществимости для ресурса M1. Количество сырья M1, соответствующего точке D = (2, 2), равно 6x1 + 4x2 = 6*2 + 4*2 = 20 т. Аналогично количество сырья, соответствующего точке G = (6, 0), равно 36 т. Таким образом, интервал осуществимости для ресурса M1 составляет 20 ≤ M1 ≤ 36 (здесь через M1 обозначено количество материала M1). Если мы определим М1 как M1 = 24 + D1, где D1 — отклонение количества материала М1 от текущего уровня в 24 т, тогда последние неравенства можно переписать как 20 ≤ 24 + D1 ≤ 36 или -4 ≤ D1 ≤ 12. Это означает, что текущий уровень ресурса M1 может быть уменьшен не более чем на 4 т и увеличен не более чем на 12 т. В этом случае гарантируется, что оптимальное решение будет достигаться в точке С — точке пересечения прямых, соответствующих ограничениям на ресурсы M1 и М2. Теперь вычислим стоимость единицы материала M1. При изменении количества сырья M1 от 20 до 36 тонн, значения целевой функции z будут соответствовать положению точки С на отрезке DG. Обозначив через y1 стоимость единицы ресурса M1, получим следующую формулу:
Если точка С совпадает с точкой D = (2, 2), то z = 5*2 + 4*2 = 18 (тысяч д.e.), если же точка С совпадает с точкой G = (6, 0), тогда z = 5*6 + 4*0= 30 (тысяч д.e.). Отсюда следует, что
Этот результат показывает, что изменение количества ресурса M1 на одну тонну (если общее количество этого ресурса не меньше 20 и не больше 36 тонн) приводит к изменению в оптимальном решении значения целевой функции на 750 д.е. Теперь рассмотрим ресурс М2.
На рис. 2 видно, что интервал осуществимости для ресурса М2 определяется концевыми точками В и H отрезка ВН, где В = (4, 0) и Н= (8/3, 2). Точка Н находится на пересечении прямых ED и ВС. Находим, что количество сырья М2, соответствующего точке В, равно x1 + 2х2 = 4 + 2*0 = 4 т, а точке Н — 8/3+2*2= 20/3 т. Значение целевой функции в точке В равно 5x1 + 4х2 = 5*4 + 4*0 = 20 (тысяч д.e.), а в точке Н — 5*8/3 + 4*2 = 64/3 (тысяч д.e.). Отсюда следует, что количество сырья М2 может изменяться от 4 до 20/3 тонн, а стоимость единицы ресурса М2, обозначенная как у2, равна
Тема 5. Применение симплекс-метода. Пример: Преобразуем следующую задачу ЛП в стандартную форму. Максимизировать z = 2x1 + 3x2 + 5x3 При выполнении условий x1 + x2 - x3 ≥ -5, -6x1 + 7x2 - 9x3 ≤ 4, x1 + x2 +4 x3 = 10, x1,x2 ≥ 0, x3 – свободная переменная. Для преобразования задачи в стандартную форму нужно: 1. Вычтем из левой части первого неравенства дополнительную (избыточную) переменную S1 и затем умножим все неравенства на -1, для того, чтобы правая часть неравенства стала положительной. (Другой путь преобразования неравенства: сначала умножим его на -1 – неравенство примет вид «≤» вместо «≥», далее к левой части неравенства прибавим дополнительную (остаточную) переменную S1). 2. Добавим дополнительную (остаточную) переменную S2, к левой части второго неравенства. При выполнении условий - x1 - x2 + x3+ - x3- + x4 = 5, -6x1 + 7x2 - 9x3+ + 9 x3- + x5 = 4, x1 + x2 +4 x3 + - 4 x3 - = 10, x1, x2, x3 +, x3 - , x4, x5≥ 0, x3 – свободная переменная. Определения базисных решений. Задача ЛП, записанная в стандартной форме, содержит m линейных равенств с n неизвестными переменными (m < n). Разделим n переменных на два множества: (1) n – m переменные, которые положим равными нулю, и (2) оставшиеся m переменные, значения которых определяются как решение системы из m линейных уравнений. Если это решение единственное, то соответствующие m переменные называются базисными, а остальные n – m нулевые переменные – небазисными. В этом случае результирующие значения переменных составляют базисное решение. Если все переменные принимают неотрицательные значения, то такое базисное решение является допустимым. В противном случае – недопустимым. Основываясь на этих определениях, нетрудно подсчитать, что количество всех положительных базисных решений для m уравнений с уравнений с n неизвестными не превосходит:
Пример: Рассмотрим следующую систему 2-х уравнений с пятью неизвестными (m=2, n=5) x1 + x2 +4x3 + 2x4 + 3x5 = 8, 4x1 +2x2 + 2x3 + x4 + 6x5 = 4. Определим различные решения этой системы. Количество положительных базисных решений равно Алгоритм симплекс- метода. Графический способ решения задачи линейного программирования (ЛП) показывает, что оптимальное решение этой задачи всегда ассоциируется с угловой точкой пространства решений. Это является ключевой идеей при разработке общего алгоритма симплекс-метода для решения задачи ЛП. Геометрический смысл этого метода состоит в последовательном переходе от одной вершины многогранника ограничений к соседней, в которой целевая функция принимает лучшее (по крайней мере, не худшее) значение (по отношению к цели задачи) до тех пор, пока не будет найдено оптимальное решение - вершина, где достигается оптимальное значение функции цели.
Для описания алгоритма симплекс-метода будем использовать симплексные таблицы. Шаг 0. Поставлена задача линейного программирования в виде: a11x1+a12x2+…+a1nxn ≤ b1 a21x1+a22x2+…+a2nxn ≤ b2 …………………………………………. am1 x1+am2x2+…+amnxn ≤ bm
F=c1x1+c2x2+…+cnxn ® max. Шаг 1. Введем добавочные переменные в ограничения, чтобы превратить неравенства в равенства. Запишем расширенную систему в виде: a11x1+a12x2+…+a1nxn +xn+1 = b1 a21x1+a22x2+…+a2nxn + xn+2 =b2 …………………………………………. am1 x1+am2x2+…+amnxn + xn+m = bm
F-c1x1+c2x2+…+cnxn =0. Шаг 2. Исходную расширенную систему заносим в первую симплексную таблицу. Последняя строка таблицы, в которой приведено уравнение для линейной функции цели, называется оценочной. В ней указываются коэффициенты функции цели с противоположным знаком: bi=-ci. В левом столбце записываем основные переменные (базис), в первой строке таблицы - все переменные (отмечая при этом основные), во втором столбце - свободные члены расширенной системы b1, b2,..., bm. Последний столбец подготовлен для оценочных соотношений, необходимых при расчете наибольшего возможного значения переменной. В рабочую часть таблицы (начиная с третьего столбца и второй строки) занесены коэффициенты aij переменных из расширенной системы. Далее таблица преобразуется по определенным правилам. Шаг 3. Проверяем выполнение критерия оптимальности при решении задач на максимум - наличие в последней строке отрицательных коэффициентов bi<0 (ci>0). Если таких нет, то решение оптимально, достигнут F=c0 (в левом нижнем углу таблицы), основные переменные равны 0, т.е. получаем оптимальное базисное решение. Шаг 4. Если критерий оптимальности не выполнен, то наибольший по модулю отрицательный коэффициент bi < 0 в последней строке определяет разрешающий столбец s. Составляем оценочные ограничения каждой строки по следующим правилам: 1)¥, если bi и ais имеют разные знаки; 2) ¥, если bi=0 и ais<0; 3) ¥, если ais=0; 4)¥, если bi =0 и ais>0; 5)çbi/ais÷, если ai0 ais имеют одинаковые знаки. Определяем min{ çbi/ais÷ }. Если конечного минимума нет, то задача не имеет конечного оптимума (Fmax= ¥). Если минимум конечен, то выбираем строку q, на которой он достигается (любую, если их несколько), и называем ее разрешающей строкой. На пересечении разрешающих строки и столбца находится разрешающий элемент aqs. Шаг 5. Переходим к следующей таблице по правилам: а) в левом столбце записываем новый базис: вместо основной переменной xq - переменную xs; б) в столбцах, соответствующих основным переменным, проставляем нули и единицы: 1- против «своей» основной переменной, 0 – в последней строке для всех основных переменных; в) новую строку с номером q получаем из старой делением на разрешающий элемент aqs; г) все остальные элементы a1ij вычисляем по правилу прямоугольника: a1ij= aij- ais aqj/ aqs. b1ij= bi- ais aqj/ aqs. Далее переходим к шагу 3.
Пример. Решим симплексным методом задачу
Решение: Нам необходимо найти начальное опорное (абсолютно произвольное) решение для функции L, которое бы удовлетворяло системе наложенных ограничений. Далее, применяя симплекс таблицы, мы будем получать решения, при которых значение функции будет, как минимум, не убывать. И так до тех пор, пока не достигнем оптимально решения, при котором функция достигает своего максимума. Если, конечно, рассматриваемая нами линейная функция обладаем максимальным значением при заданной системе ограничений. Перед применением симплекс таблиц, необходимо преобразовать систему линейных ограничений и рассматриваемую нами функцию L к вполне определенному виду: · Свободные члены системы ограничений должны быть неотрицательными; · Система ограничений должна быть приведена к каноническому виду.
Ø К левой части неравенства 1 системы ограничений прибавляем неотрицательную переменную x4 - преобразуем неравенство 1 в равенство.
Ø К левой части неравенства 2 системы ограничений прибавляем неотрицательную переменную x5 – преобразуем неравенство 2 в равенство. Ø К левой части неравенства 3 системы ограничений прибавляем неотрицательную переменную x6 – преобразуем неравенство 3 в равенство.
Система ограничений приведена к каноническому виду, т.е. все условия системы представляют собой уравнения.
2. Определимся с начальным опорным решением. Наличие единичного базиса в системе ограничений позволяет легко найти начальное опорное решение. Подробнее: · Переменная x4 входит в уравнение 1 с коэффициентом 1, а в остальные уравнения системы с коэффициентом ноль, т.е. x4 - базисная переменная; · Переменная x5 входит в уравнение 2 с коэффициентом 1, а в остальные уравнения системы с коэффициентом ноль, т.е. x5 – базисная переменная; · Переменная x6 входит в уравнение 3 с коэффициентом 1, а в остальные уравнения системы с коэффициентом ноль, т.е. x6 - базисная переменная; Переменные, которые не являются базисными, называются свободными переменными. Приравняв свободные переменные нулю, в получившейся системе ограничений мы получим начальное опорное решение. X нач = (0, 0, 0, 25, 20, 18)
Вернемся к рассмотрению функции L. Функция L не содержат базисных переменных. Для составления начальной симплекс таблицы мы выполнили все условия. В процессе дальнейших преобразований возможны два случая: 1. Если в симплекс таблице, на каком-то шаге, мы получим строку L состоящую из неотрицательных элементов - задача решена, мы нашли оптимальное решение. 2. В противном случае - функция не является ограниченной. Обратите внимание: Шаг 1: За ведущий выберем столбец 3, так как -9 наименьший элемент в L строке. Элемент L строки, принадлежащий столбцу свободных членов не рассматриваем. За ведущую выберем строку 3, так как отношение свободного члена к соответствующему элементу выбранного столбца для 3 строки является наименьшим. Обратите внимание, что отношение мы вычисляем только для положительных элементов столбца 3.
Разделим элементы строки 3 на 3.
От элементов строки 1 отнимает соответствующие элементы строки 3, умноженные на 3. От элементов строки 2 отнимает соответствующие элементы строки 3, умноженные на 2. От элементов строки L отнимает соответствующие элементы строки 3, умноженные на -9.
X 1 = (0, 0, 6, 7, 8, 0)
Значение функции L для данного решения: L (X 1) = 54 Шаг 2: За ведущую выберем строку 2, так как отношение свободного члена к соответствующему элементу выбранного столбца для 2 строки является наименьшим. Обратите внимание, что отношение мы вычисляем только для положительных элементов столбца 2.
Разделим элементы строки 2 на 6
От элементов строки 1 отнимает соответствующие элементы строки 2, умноженные на 2. От элементов строки L отнимает соответствующие элементы строки 2, умноженные на -5.
X 2 = (0, 4/3, 6, 13/3, 0, 0)
Значение функции L для данного решения: L (X 2) = 182/3 Учитывая, что все x i Теперь можно записать ответ: X опт = (0, 4/3, 6, 13/3, 0, 0)
М-метод. Пусть задача ЛП записана в стандартной форме. Для любого равенства i, в котором не содержится дополнительная остаточная переменная, введем искусственную переменную Ri, которая далее войдет в начальное базисное решение. Но, поскольку эта переменная искусственна (другими словами, не имеет никакого "физического смысла" в данной задаче), необходимо сделать так, чтобы на последующих итерациях она обратилась в нуль. Для этого в выражение целевой функции вводят штраф. Переменная Ri, с помощью достаточно большого положительного числа М штрафуется путем ввода в целевую функцию выражения -MRi в случае максимизации целевой функции и выражения +MRi, — в случае минимизации. Вследствие этого штрафа естественно предположить, что процесс оптимизации симплекс-метода приведет к нулевому значению переменной Ri. Следующий пример проясняет детали этого метода. Пример. Минимизировать При выполнении условий
Стандартная форма этой задачи получается в результате добавления дополнительной (избыточной) переменной х3 во второе неравенство и дополнительной (остаточной) переменной х4 в третье неравенство. Эта задача в стандартной форме будет записана следующим образом: Минимизировать z = 4x1 + х2 При выполнении условий
В полученной задаче первое и второе уравнения не имеют дополнительных (остаточных) переменных, которые можно ввести в базисное решение. Поэтому введем в эти уравнения искусственные переменные R1 и R2, а в целевую функцию добавим штраф MRl + MR2. В результате получим следующую задачу ЛП. Минимизировать При выполнении условий
В этой модифицированной задаче переменные R1 и R2 и х4 можно использовать в качестве начального допустимого базисного решения. В результате получим следующую симплекс-таблицу.
Прежде чем применять симплекс-метод, надо согласовать значения в z-строке с остальной частью таблицы. В частности, значение функции z, соответствующее начальному базисному решению R1 = 3, R2 = 6 и х4 = 4, должно равняться ЗМ+ 6М + 0 = 9M, а не 0, как показано в таблице. Это противоречие связано с тем, что переменным R1 и R2 соответствуют ненулевые коэффициенты (-М, -М) в строке z. Чтобы сделать эти коэффициенты нулевыми, следует умножить элементы строк R1 и R2 на величину М, и затем сложить эти строки с z-строкой. (Обратите внимание на "подсвеченные" единицы в этих строках — если бы эти коэффициенты были отличны от единиц, то необходимо было бы сначала разделить все элементы этих строк на данные коэффициенты). Кратко это действие можно записать следующим образом. Новая z-строка = старая z-строка + М х R1-строка + М х R2-строка Измененная симплекс-таблица примет следующий вид:
Отметим, что теперь z = 9М, что соответствует базисному решению R1 = 3, R2 = 6 и x4 =4. Последняя таблица готова к применению симплекс-метода с использованием условий оптимальности и допустимости. Поскольку мы минимизируем целевую функцию, находим наибольший положительный коэффициент в z-строке. Наибольший коэ |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 912; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.158.111 (0.017 с.) |


 (тысяч д.е. на тонну материала M1).
(тысяч д.е. на тонну материала M1).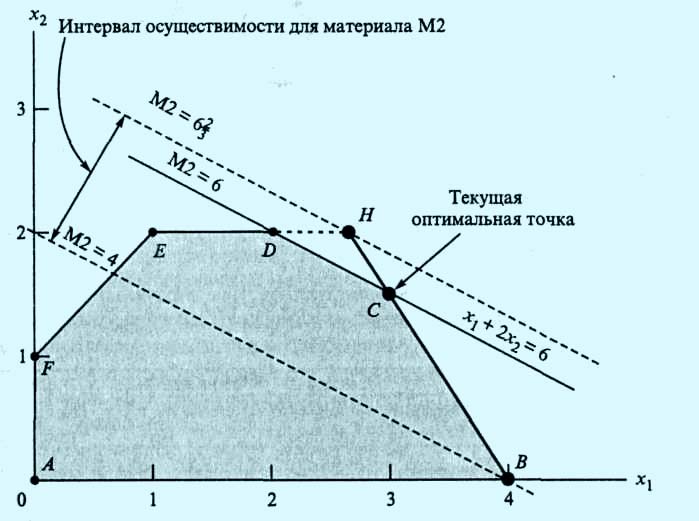
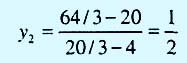 (тысяч д.е. на тонну материла M2).
(тысяч д.е. на тонну материла M2).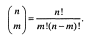
 Ниже покажем, что некоторые из этих решений на самом деле не будут базисными.
Ниже покажем, что некоторые из этих решений на самом деле не будут базисными.

 0, по условию задачи, наибольшее значение функции L равно свободному члену 182/3, т.е. мы получили оптимальное решение.
0, по условию задачи, наибольшее значение функции L равно свободному члену 182/3, т.е. мы получили оптимальное решение.