Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оценка достоверности средних арифметических и относительных величинСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
При изучении сплошной (генеральной) совокупности для ее числовой характеристики достаточно рассчитать М и δ. На практике, как правило, мы имеем дело не с генеральной, а с выборочной совокупностью. Для выборочного метода очень важен способ отбора части от целого, так как отобранная часть, как уже упоминалось ранее, должна быть репрезентативной. При выборке возможны ошибки смещения, то есть такие события, появление которых не может быть точно предсказуемым..Вместе с тем, они являются закономерными, объективными, так и необходимыми. При определении степени точности выборочного исследования оценивается величина ошибки, которая может произойти в процессе выборки. Такие ошибки носят название случайных ошибок репрезентативности (т) и являются фактической разностью между средними или относительными величинами, полученными при выборочном исследовании, и аналогичными величинами, которые были бы получены при изучении всей совокупности. Средняя ошибка среднего арифметического числа определяется по формуле: Среднюю ошибку средней арифметической величины можно вычислить как и сигму, по амплитуде вариационного ряда:
S — коэффициент для определения ошибки, соответствующий числу наблюдений (см. табл. 5.10). В приведенном примере (из табл. 5.8) средняя ошибка составила ±0,16 дней.
А при расчете по амплитуде вариационного ряда: Дней, что достаточно близко к средней ошибке, рассчитанной по обычной формуле. При оценке полученного результата по размеру средней ошибки пользуются доверительным коэффициентом (t), который дает возможность определить вероятность правильного ответа, то есть он указывает на то, что полученная величина ошибки выборки будет не больше действительной ошибки, допущенной вследствие сплошного наблюдения. Так, если принять t = 2,6, то вероятность правильного ответа составит 99,0%, а это означает, что из 100 выборочных наблюдений только один раз выборочная средняя может оказаться вне пределов генеральной средней. При t = 1 вероятность правильного ответа составит лишь 68,3%, а 31,7% средних могут оказаться вне вычисленных пределов. Следовательно, с увеличением доверительной вероятности увеличивается ширина доверительного интервала, что, в свою очередь повышает достоверность суждения, спорность полученного результата (табл. 5.11).
Таблица 5.10 Вычисление сигмы (δ) и средней ошибки (m) по амплитуде
Таблица 5.11 Оценка полученного результата по средней ошибке
В медико-статистических исследованиях обычно используют доверительную вероятность (надежность); равную 95,5 — 99,9%, а в наиболее ответственных случаях — 99,7%. Таким образом, если δ является доверительной вероятностью появления необходимых данных в заданных границах, то является доверительным интервалом, с помощью которого определяются границы возможного размера изучаемого явления. Зная размер ошибки, можно, как отмечалось выше, правильно определить требуемое число наблюдений для выборочного исследования при помощи преобразования формулы предельной ошибки выборки Δ (дельта) =
Решая приведенное равенство относительно п, получим формулу для определения числа наблюдений: Для примера воспользуемся Определяем требуемое число наблюдений:
Вывод: для того, чтобы оперировать в использованном нами примере с указанной точностью (99,7%), следует подвергнуть изучению 95—96 больных. Нами исследовано 95 больных, что соответствует искомой величине.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 461; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.34.105 (0.008 с.) |

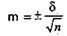
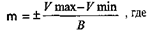
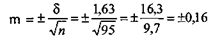
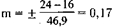
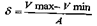
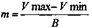
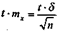 , в которую входит величина п — число наблюдений.
, в которую входит величина п — число наблюдений.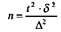 данными изучения средней длительности пребывания больных в специализированном отделении. Здесь М = 20 дн., δ = ±1,63дн., m = +0,16 дн. Сколько же нужно дополнительно исследовать больных, заведомо оперируя ошибкой выборки больше полученной (Δ = ±0,5дн.), при доверительной вероятности t = 3.
данными изучения средней длительности пребывания больных в специализированном отделении. Здесь М = 20 дн., δ = ±1,63дн., m = +0,16 дн. Сколько же нужно дополнительно исследовать больных, заведомо оперируя ошибкой выборки больше полученной (Δ = ±0,5дн.), при доверительной вероятности t = 3.