
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Схема оценки тесноты корреляционной связи по коэффициенту корреляцииСодержание книги
Поиск на нашем сайте
Приведем пример вычисления коэффициента корреляции по приведенной формуле (см. табл. 5.15). • Ход вычислений здесь чрезвычайно прост. Суммируя ряды х и у, получаем Таблица 5.15 Корреляция между среднемесячной температурой воздуха И числом умерших детей до 1 года от кишечных заболеваний (в одной из стран Центральной Азии)
Подставляем значения сумм этих рядов в формулу:
получим:
То есть, между среднемесячной температурой воздуха и числом умерших от острых кишечных инфекций существует прямая корреляционная связь. Это чрезвычайно простое для понимания вычисление требует довольно кропотливой, хотя и несложной математической работы. Вычислительная работа особенно затрудняется тогда, когда члены коррелируемых рядов имеют большие числовые значения, особенно, если варианты коррелируемых рядов приведены в виде сгруппированных интервалов и, следовательно, приходятся вычислять не простую, а взвешенную среднюю. Средняя ошибка коэффициента корреляции. Поскольку коэффициент корреляции в клинических исследованиях рассчитывается обычно для ограниченного числа наблюдений, нередко возникает вопрос о надежности полученного коэффициента. С этой целью определяют среднюю ошибку коэффициента корреляции. При достаточно большом числе наблюдений (больше 100) средняя ошибка коэффициента корреляции (mr) вычисляется по формуле: п — число наблюдений. В том случае, если число наблюдений меньше 100, но больше 30, точнее определять среднюю ошибку коэффициента корреляции, пользуясь формулой:
С достаточной для медицинских исследований надежностью о наличии той или иной степени связи можно утверждать только тогда, когда величина коэффициента корреляции превышает или равняется величине трех своих ошибок (
Если Дисперсионный анализ Дисперсионный анализ позволяет дать обобщенную характеристику трем и более средним величинам или показателям и позволяет: — измерить силу влияния; — оценить разность частных средних или показателей; — определить достоверность разности частных средних или показателей. Дисперсионный анализ показывает степень рассеивания вариации (дисперсии) измеряемых признаков вокруг среднего типичного уровня, поэтому он дает возможность изучить действие на конечный результат исследования нескольких факторов вместе, роль каждого из них и сравнить действие отдельных факторов между собой. Изучение действия факторов производится путем сравнения средних значений наблюдаемого признака, полученных в результате воздействия каждого из этих факторов при разном их сочетании. Различают следующие виды дисперсионного анализа: однофакторный, двухфакторный и многофакторный. Методика проведения дисперсионного анализа изложена в многочисленных специальных изданиях по медицинской статистике. Непараметрические критерии Непараметрические критерии используются преимущественно в тех случаях, когда изучаемое явление отличается от нормального распределения. С одной стороны, они позволяют оценить характер, тенденцию явления (увеличение, уменьшение, без перемен), хотя, с другой, большинство из них обладает достоверно высокой статистической мощностью (чувствительностью). Особенно эффективно применение непараметрических критериев при малых выборках (п <30), при изучении качественных признаков. Преимуществом большинства непараметрических критериев является сравнительная простота расчетов. Основные направления применения непараметрических критериев: 1. Для характеристики одной совокупности: — критерий итераций (флуктуации); — медиана, квартели. 2. Для оценки связи между явлениями: — коэффициент ранговой корреляции (Спирмена); — коэффициент корреляции рангов (Кэндела); — показатель соответствия χ2 (хи-квадрат).. 3. Для оценки различий двух сравниваемых совокупностей. При этом следует выделять несколько вариантов: 1. Для сравнения количественных признаков:
2. Для сравнения качественных признаков:
Конкретные не параметрические критерии подробно изложены в специальных руководствах по медицинской статистике.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 338; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.15.34 (0.006 с.) |

 х = 119 и
х = 119 и  и
и  , aпреумножая попарно числа рядов dx и dy между собой, получаем ряд dx • dy.
, aпреумножая попарно числа рядов dx и dy между собой, получаем ряд dx • dy.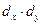
 =119
=119
 = 9,9
= 9,9
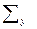 =105,2
Му =
=105,2
Му =  = 8,8
= 8,8
 =
406,92
=
406,92
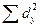 =
162,44
=
162,44
 =
178,32
=
178,32

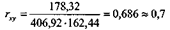

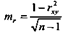
 3mr). Обычно это отношение коэффициента корреляции (
3mr). Обычно это отношение коэффициента корреляции ( ) к его средней ошибке (mr) обозначают буквой t и
) к его средней ошибке (mr) обозначают буквой t и
 3, то коэффициент корреляции достоверен.
3, то коэффициент корреляции достоверен. ) Критерий Вилкоксона— Манна-Уитни(И) Критерий Мостселлера
) Критерий Вилкоксона— Манна-Уитни(И) Критерий Мостселлера



