
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Достоверность показателей и разности показателейСодержание книги
Поиск на нашем сайте
Достоверность показателя определяется с помощью его средней ошибки по формуле: Например: обследовано 1800 больных, из них выявлено 90 больных гипертонической болезнью I ст. Процент выявленных больных по данным проведенного осмотра равен:
Следовательно, с вероятностью 95,5% показатель выявляемости больных с ГБ-1 в аналогичных условиях будет колебаться в пределах Р±2т = 5 ± 2 • 0,5 = 5± 1,0, то есть от 4 до 6 случаев на 100 обследованных. Достоверность различий между сравниваемыми показателями вычисляется по формуле, аналогичной для средних величин:
Оценивается критерий различия показателей так же, как и средних величин. Для примера сопоставим уровни общей летальности в двух больницах:
Определим средние ошибки показателей:
Вычисляем критерий различия:
Рассчитанный критерий различия равен 2,6, то есть больше 2, что указывает на достоверною, не случайную, статистически значимую разницу уровней летальности в сравниваемых больницах. Оценка нулевого эффекта. При альтернативном распределении (либо-либо), когда показатель равен нулю (Р = 0) или близок к нулю, a q = 100% или когда показатель равен 100% (Р = 100%) или близок к 100%, a q = 0, следует узнать, а каким бы мог быть показатель изучаемого явления при других условиях отбора (другое число наблюдений, другой состав больных по полувозрасту и т.д.)? Для этого пользуются специальной формулой, по которой можно вычислить, «ожидаемый» уровень показателя:
а — результативный показатель (Р). Допустим, что в больнице лечилось экспериментальным методом 60 больных (п), среди которых летальных исходов не было (P =0%). Вычисляем «ожидаемый» показатель летальности:
Ошибка такого показателя определяется по формуле: При t = 2 возможны колебания ожидаемого показателя в пределах от 0% до 4,78% (1,6 ±3,18). Малая выборка В клинических и экспериментальных работах довольно часто приходится пользоваться малой выборкой, когда,число наблюдений меньше 30. При такой выборке средние величины и показатели вычисляются по тем же формулам, что и при большой. При вычислении среднего квадратического отклонения и средней ошибки показателя число наблюдений уменьшается на единицу:
Достоверность результатов (t) оценивается по таблице 5.12. Обращаться с таблицей Стьюдента следует по графе 1 -и, в которой указано число степеней свободы (п), равное п —1, то есть числу проведенных наблюдений уменьшенному на единицу. Данные 2, 3, и 4-й граф исчислены для вероятности правильного заключения, равной: 95% — графа 2, при риске : ошибки 5% (Р05); 99% - графа 3, при риске ошибки 1 % (Р01) и 99,9% -графа 4, при риске ошибки 0,1 % (Р001). Методы измерения между явлениями Корреляционный анализ Одной из важных задач исследовательской работы является выявление и измерение связи между признаками, характеризующими изучаемые явления или процессы. Различают функциональную и корреляционную связи. При наличии функциональной связи изменение величины одного признака неизбежно вызывает совершенно определенные изменения величины другого признака. Примером такой связи может служить зависимость площади круга от его радиуса. Функциональная связь между явлениями присуща неживой природе. В биологических науках чаще приходится иметь дело с иной связью между явлениями, когда одной и той же величине одного признака соответствует ряд варьирующих значений другого признака, что обусловлено чрезвычайным многообразием взаимодействия различных явлений живой природы. Такого рода связь носит название корреляционной (correlation — соответствие, соотносительность). В то время, как функциональная связь имеет место в каждом отдельном наблюдении, корреляционная связь проявляется только при многочисленном сопоставлении признаков. Рассмотрим, например, связь между возрастом детей-дошкольников и их ростом. Из приведенных данных видно, что с возрастом рост детей увеличивается, и поэтому можно предположить наличие связи между указанными признаками. Таблица 5.13
Вместе с тем, следует отметить, что одному и тому же возрасту соответствует различный рост детей. Это происходит потому, что рост детей определяется не только возрастом, на него влияют многие другие секторы, в том числе условия жизни, питание, занятия физкультурой и др. Таким образом, можно прийти к выводу, что связь между возрастом и ростом детей является корреляционной.
Исследователю следует помнить, что обнаружение корреляции между сопоставляемыми явлениями не говорит еще о существовании причинной связи между ними. Для установления последней необходим всесторонний логический и специальный анализ существа изучаемых процессов. Статистический же метод позволяет обосновать полученные в результате научного исследования выводы о наличии тех или иных связей между явлениями, выделить самые главные из них. Сила связи между явлениями, ее теснота и направленность определяются величиной коэффициента корреляции, который колеблется в пределах от 0 до
По направленности связь между явлениями может быть прямой (положительной), когда с увеличением (уменьшением) значений одного признака увеличиваются (уменьшаются) значения другого (то есть, когда признаки меняются в одном направлении), и обратной (отрицательной), когда с увеличением значений одного признака значения другого уменьшаются и наоборот (то есть, изменения признаков — разнонаправленны). Таблица 5.14
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 404; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.212.14 (0.012 с.) |

 , где р - размер показателя, выраженный в долях единицы, в процентах, в промилле; q - равно 1 - р или 100 - р или 1000- р (величина, дополняющая показатель до основания); п — число наблюдений.
, где р - размер показателя, выраженный в долях единицы, в процентах, в промилле; q - равно 1 - р или 100 - р или 1000- р (величина, дополняющая показатель до основания); п — число наблюдений. = 5 случаев на 100 осмотренных.
= 5 случаев на 100 осмотренных.




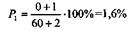


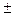 1. При r = 0 связь отсутствует, при r =
1. При r = 0 связь отсутствует, при r = 



