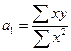Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Динамика численности больничных коек в стационарах системы МЗ РФ санкт-петербургаСодержание книги
Поиск на нашем сайте
2) Показатель наглядности: 1990г. — 100% 1991 58,5-100 1992 58,5-100 53,9 - х 51,1-х х = 92,1 х=87,4
1993 58,5-100 1994 58,5-100 49,3 - х 47,5-х х = 84,3 х=81,7
3)Показатели роста (убыли): 1991 58,5-100 1992 53,9-100 53,9 - х 51,1-х х = 92,1 х=94,8 1993 51,1 - 100 1994 49,3-100 49,3-х 47,8 - х х = 96,5 х=96,9 4)Темп прироста (убыли): 1991 58,5-100 1992 53,9 - 100 -4,6 - х -2,8 - х х= -7,9 х = -5,2
1993 51,1 – 100 1994 49,3-100 -1,8 - х -1,5 - х х = - 3,5 х= - 3,1
Рассчитанные показатели динамического ряда свидетельствуют об убыли числа больничных коек в Санкт-Петербурге, однако темп их убыли снижается. Выравнивание динамического ряда Иногда динамика изученного явления представлена не в виде непрерывно меняющегося в одном направлении явления, а скачкообразными изменениями. В таких случаях используют различные методы выравнивания динамического ряда: — укрупнение интервалов; — расчет скользящей средней; — метод наименьших квадратов. Укрупнение материала можно производить за определенные промежутки времени (за квартал, за один, два, три года и т.д.). Пример выравнивания динамического ряда с помощью укрупнения интервалов приведены в таблице 5.5.
Таблица 5.5 Динамика средней длительности пребывания больного На терапевтической койке до— и при переходе больниц Санкт-Петербурга на новые условия хозяйствования
Произведено укрупнение интервала за два года и рассчитана средняя длительность пребывания больного на койке для каждого интервала. 1987-1988 (19,9+19,9)/2=19,5 1989-1990 (19,2+19,3)/2=19,3 1991-1992 (18,5+17,0)/2=17,8 Показатели преобразованного динамического ряда рассчитываются по общепринятой методике. Влияние случайных колебаний на уровни динамического ряда можно устранить и с помощью скользящей средней. При ее расчете лучше использовать интервалы, включающие три хронологические периода. Пример выравнивания динамического ряда методом скользящей средней в таблице 5.6. Таблица 5.6 Динамика средней длительности пребывания больного На терапевтической койке до— и при переходе стационаров Санкт-Петербурга на новые условия хозяйствования
Для выравнивания динамического ряда произведено вычисление скользящей средней с использованием интервала в три года: 1988г. (19,9+19,0+19,2)/3=19,4 1989г. (19,0+19,2+19,3)/3=19,2 1990г. (19,2+19,3 +IВ,5)/3= 19,0 1991г. (19,3+18,5+17,0)/3=18,3 Однако этот метод исключает из анализа средние величины первого и последнего уровня. Поэтому для более точного определения тенденции изучаемого явления можно рассчитать скользящие средние крайних уровней по формуле Урбаха: 1987 г. (7у1 + 4у2 - 2у3) /9= (7 • 19,9 + 4 • 19 - 2 • 19,2) / 9 = 19,7 1992 г. (7у6 + 4 у5 - 2у4) / 9 = (7 • 17,0 + 4 • 18,5 - 2 • 19,3) / 9 = 17,2 Метод наименьших квадратов дозволяет наиболее точно выравнивать тенденции изучаемого явления. Он позволяет рассчитать точки прохождения такой прямой линии, от которой имеющаяся эмпирическая находится на расстоянии наименьших квадратов от других возможных линий. Динамический ряд в случае применения данного метода должен иметь не менее 5 хронологических дат, количество их должно быть нечетным, а интервалы между ними — одинаковыми. Пример выравнивания динамического ряда методов наименьших квадратов приведен в таблице 5.7. Таблица 5.7 Динамика младенческой смертности в Санкт-Петербурге (на 1000 родившихся живыми) за 1988—1992 гг.
Дата искомой прямой линии округляются по следующей формуле: У1 = а0 + а1 · х, где а0 — это хронологическая средняя (значение центральной хронологической даты), которая вычисляется по формуле:
S — сумма хронологических дат (периодов);
87,3 а0 = ----------------- =17,5 а1 — это коэффициент поправки искомого расстояния, который определяется по формуле:
х — порядковый номер (расстояние) хронологических дат от центральной, принятой за 0. Сумма произведений х-у определяется с учетом алгебраических знаков.
Зная величины а0 и а1, подставляем их в уравнение: у1 = а0 + а1 ·х и, придавая последовательные значения чисел ряда х, получим выравненный динамический ряд младенческой смертности. 1988 у1 = 17,5 + (-0,75)· (-2) = 19 1969 у2 = 17,5 + (-0,75)·(-1)= 18,3 1991 у4= 17,5 + (-0,75)·(1) = 16,8 1992 у5= 17,5 + (-0,75)·(2)= 16,0
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 558; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.118.236 (0.01 с.) |

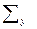 = 87,3
= 87,3
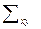 =-7,5
=-7,5
 х2 = 10
х2 = 10

 — сумма всех значений изучаемого явления.
— сумма всех значений изучаемого явления.