
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Концентрация напряжений и её влияние на прочностьСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Что такое, концентрация напряжений? Рассмотрим пример. При растяжении призматического бруса, напряжения по его сечению распределяются равномерно (рис. 4.11, а). А далее рассмотрим брус с выточкой. В этом случае эпюра напряжений в наименьшем сечении бруса имеет вид (рис. 4.11, б) Покажем σ ном – номинальные напряжения – это напряжения, вычисляемые в предположении отсутствия концентрации напряжений по обычным формулам сопротивления материалов
Превышение местными напряжениями номинальных напряжений называется концентрацией напряжений, а места нарушения призматической формы называются концентраторами напряжений. Здесь концентратор напряжения – выточка, в других случаях – резьба, галтель, отверстия и так далее.
Коэффициент αр зависит от резкости концентратора напряжений, от размеров концентратора напряжений и детали, от типа деформации и от вида концентратора напряжений. Если речь идёт о мелкой выточке, то его (концентрация) резкость определяется двумя параметрами (рис. 4.12): глубиной выточки t и радиусом кривизны ρ у дна выточки (от вида концентратора, тоже), точнее, от отношения t /ρ. При увеличении этого отношения αр возрастает. Как определить αр. Можно теоретическим путём, решая соответствующую задачу математической теории упругости. Определяют и экспериментальным путём, например, методом просвечивания оптически активных материалов, методом лакокрасочных покрытий, методом тензометрирования. В настоящее время изучены многие концентраторы напряжений и для них, в справочной литературе, приведены значения теоретических коэффициентов концентрации напряжений αр. Если p max > p т, то коэффициент концентрации будет меньше αр. В этом случае вводится понятие эффективного коэффициента концентрации напряжений, который обозначается через (к σ, к τ). Что такое кр?
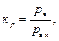
где р в – разрушающее напряжение для детали без концентратора напряжений; р в к – разрушающее напряжение для детали с концентратором напряжений, но вычисляемое, по номинальным напряжениям. Иначе говоря, кр – это отношение разрушающих нагрузок для образцов без концентраторов напряжений и с концентраторами напряжений. Иногда кр называют действительным коэффициентом концентрации напряжений. Как влияет концентратор напряжения на прочность? 1 случай: напряжения постоянны, деталь из пластичного материала (рис. 4.13, а). Главное здесь – разрушение наступает после больших пластических деформаций и поэтому, распределение напряжений с увеличением нагрузки ведёт себя следующим образом: если σ наиб < σ т, то эпюра напряжений имеет вид (рис. 4.13, б); если σ наиб > σ т, то эпюра будет иметь вид (рис. 4.13, в) и наконец, перед разрушением, когда σ наиб = σ в, разницы между местными и наибольшими напряжениями не будет (рис. 4.13, г), тогда кσ = 1, а расчёт на прочность следует вести, по σ ном. 2 случай: напряжения постоянны, а деталь из хрупкого материала. Диаграмма напряжений для хрупкого материала, имеет вид В этом случае выравнивания напряжений не происходит и как только местные напряжения достигнут р в, то есть р наиб =αр·р ном = р в – произойдёт разрушение.
Но здесь, есть исключение: серый чугун, хотя этот материал и является хрупким. Для серого чугуна, который содержит графитовые включения, кр = 1, то есть, в деталях с концентраторами напряжений, будут такие же разрушающие нагрузки, как и без концентраторов напряжений. Это происходит потому, что графитовые включения являются более резкими концентраторами напряжений, чем конструктивные концентраторы и они, всё определяют. 3 случай: напряжения переменны, деталь из пластичного материала. Будем пока говорить о напряжениях, изменяющихся по симметричному циклу. Начнём с кр
где p –1 – предел выносливости образца без концентратора напряжений, p –1 к – предел выносливости образца с концентратором напряжений. Деталь из пластичного материала, поэтому, казалось бы, должен быть эффект выравнивания напряжений по сечению детали. Он есть, но проявляется частично, поэтому 1 < кр < αр. Для низкопрочных и высокопластичных материалов кр приближается к 1, а для высокопрочных и малопластичных, кр ближе к αр. Таким образом, у каждого материала, своя чувствительность к концентраторам напряжений. В связи, с этим вводится, так называемый коэффициент чувствительности к концентраторам напряжений, который обозначается, через q р:
От чего зависит q р? Главным образом, от материала. С ростом σ в, увеличивается и q р; q р зависит, от размеров детали: с ростом диаметра, увеличивается, и q р; q р зависит от резкости концентратора напряжений: с увеличением αр также растёт q р, так как возрастает быстрее, чем αр. В каких пределах изменяется q р? 0 < q р < 1. Для низкопрочных и пластичных материалов, q р приближается к нулю, а для высокопрочных – к единице. Для q р имеются данные в справочниках и по нему находится: кр = 1 + q р ·(αр – 1). Однако, по этой формуле получаются не очень точные значения кр, поэтому для наиболее распространённых концентраторов напряжений, лучше брать кр, из справочников. Если же концентратор новый, и для него известно только αр, то приходится пользоваться, этой формулой. Таким образом, расчёт на прочность деталей из пластичных материалов при переменных напряжениях нужно вести, по номинальным напряжениям, увеличенным в кр раз, что следует из формулы 4 случай: напряжения переменны, деталь из хрупкого материала. Так как деталь из хрупкого материала, то пластических деформаций нет, выравнивания напряжений по сечению нет, и быть не может, поэтому кр = αр, тогда q р = 1. Это предельный случай. Здесь тоже исключение для серого чугуна – q р = 0, кр = 1. Таким образом, при переменных напряжениях, для деталей из хрупкого материала, расчёт на прочность нужно вести по местным напряжениям, то есть с допускаемыми напряжениями нужно сравнивать р наиб =αр·р ном. 4.5. Предел выносливости детали Предел выносливости детали также определяется экспериментальным путём. Оборудование применяется, несомненно, более сложное. Чаще, испытания ведут на вибростендах. Предел выносливости деталей отличается от предела выносливости материала, так как детали имеют концентраторы напряжений, бóльшие размеры, обработку, отличную от полирования, подвергаются упрочнению и другие факторы (работа в коррозионной среде, в вакууме и так далее). Чаще всего, приходится учитывать четыре фактора: 1) концентраторы напряжений; 3) размеры поперечного сечения; 3) шероховатость поверхности; 4) поверхностное упрочнение. С учётом этих четырёх факторов, предел выносливости детали при симметричном цикле, вычисляется по следующей формуле:
Здесь p - 1 – предел выносливости материала; k р – эффективный коэффициент концентрации напряжений; kd – коэффициент влияния абсолютных размеров поперечного сечения – это отношение предела выносливости гладких образцов диаметром d к пределу выносливости гладких стандартных образцов. Этот коэффициент зависит: 1) от поперечных размеров детали – при увеличении поперечного размера коэффициент kd возрастает, 2) от предела прочности материала – при увеличении σ в коэффициент kd уменьшается, 3) от коэффициента концентрации напряжений – при увеличении k р коэффициент kd уменьшается. 0,5 ≤ kd ≤ 1; kF – коэффициент влияния шероховатости поверхности – это отношение предела выносливости образцов с данной шероховатостью поверхности к пределу выносливости стандартных (полированных) образцов. Этот коэффициент зависит: 1) от вида обработки поверхности: чем тщательнее обработана поверхность, тем он выше; 2) коэффициент kF зависит от материала: при увеличении предела прочности материала, kF уменьшается, так как с увеличением σ в шероховатость, как концентратор напряжения, сказывается, в большей степени; величина коэффициента kF < 1. kv – коэффициент влияния поверхностного упрочнения – отношение предела выносливости упрочнённых образцов к пределу выносливости неупрочненных образцов. Этот коэффициент зависит: 1) от вида упрочняющей обработки, 2) от материала - при увеличении предела прочности материала kv возрастает, 3) от коэффициента концентрации напряжений - при увеличении k р возрастает и kv. величина коэффициента kv > 1. 4.6. Предел выносливости детали И в этом случае, предел выносливости детали определяется экспериментальным путём. Провести эти эксперименты, естественно, сложнее, чем при симметричном цикле. Таких проведённых опытов, сравнительно мало. Те же опыты, которые проведены, показали, что концентрация напряжений, размеры детали, шероховатость поверхности и упрочнение поверхности оказывают влияние только на переменную составляющую цикла напряжений и влияют эти факторы на переменную составляющую так же, как и при симметричном цикле. Эти коэффициенты приведены в справочниках. Всё вышесказанное, касается деталей из пластичных материалов. Детали из хрупких материалов мы не рассматриваем, так как их в авиации нет, но для деталей из хрупких материалов, указанные факторы оказывают влияние и на постоянную составляющую цикла напряжений. Изобразим диаграмму предельных амплитуд цикла для материала (рис. 4.15, а). Обозначения – общие: Mr – точка, соответствующая одному из предельных циклов, Далее изобразим диаграмму предельных амплитуд цикла для деталей из пластичного материала (рис. 4.15, б). Две точки нам первая точка – при
Вторая точка — при 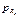 = 0, = 0, 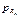 = p в – статическое нагружение. Эта запись справедлива только для деталей из пластичного материала. Для деталей из хрупкого материала второй точкой будет не = p в – статическое нагружение. Эта запись справедлива только для деталей из пластичного материала. Для деталей из хрупкого материала второй точкой будет не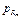 , = p в, а , = p в, а 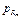 = p в /αр. = p в /αр.
Промежуточные точки получим, используя диаграмму предельных амплитуд цикла для материала. Откладываем значение Для вывода расчётных зависимостей необходимо представить диаграмму предельных амплитуд, теоретически. При этом, кривую, заменим прямой. На практике применяются две схематизации: Схематизация 1 (рис. 4.16, а) (на рисунке – штриховая линия) – применяется для расчета стационарных машин. По этой схематизации возможности материала занижены. При расчёте деталей летательных аппаратов и их двигателей, применяется более точная схематизация 2 (рис. 4.16, а – сплошная прямая), предложенная советскими учёными С.В. Серенсеном и Р.С. Кинасошвили (ЦИАМ). В первой части диаграммы, возможности детали занижены незначительно, во второй – завышены, но они не используются, так как там, опасными являются, напряжения по текучести. Рассмотрим подробно схематизацию 2. Вначале для материала. За предельный цикл, через который производится схематизация, принимается положительный отнулевой цикл (рис. 4.16, б).
Точка M 0 (рис. 4.16, б) соответствует от нулевому циклу, при этом цикле предел выносливости – р 0, тогда 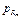 = = 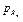 = р 0/2, = р 0/2, 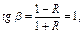 следовательно, β = 45°. следовательно, β = 45°.
Под углом 45° из начала координат проводим прямую до пересечения с предельной кривой, а также прямую 2 из точки А через полученную точку М 0. Почему, через эту точку? Потому что, во-первых, она проходит возле границы, до которой используется диаграмма и, во-вторых, предел выносливости при отнулевом цикле является основной механической характеристикой, которая так же, как и p -1, определяется сравнительно просто при испытаниях на усталость (но первая причина, является наиболее важной). Таким образом, по результатам испытаний при симметричном и от нулевом циклах мы получили схематизированную диаграмму предельных амплитуд цикла напряжений для материала. Теперь перейдём, к диаграмме предельных амплитуд цикла напряжений для детали из пластичного материала (рис. 4.17). Следует обратить внимание на то, что для детали точка, через которую проходит схематизированная прямая, – это уже не соответствует положительному отнулевому циклу. Для дальнейших выводов удобнее пользоваться отрезком ОЕ. Выведем формулу для этого отрезка:
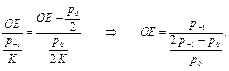
Обозначим: ψр = Чем больше ψр, тем меньше ОЕ, тем в большей степени предельная амплитуда убывает в зависимости от асимметрии цикла. Окончательно:
где ψр – новая механическая характеристика материала f (p - 1, p 0, ψр). ψр зависит: 1) прежде всего. от материала – чем выше предел прочности p в тем больше, то есть чем выше прочность материала, тем более он чувствителен, к асимметрии цикла; 2) от типа деформации (для одного и того же материала ψσ ≈ 2· ψτ). Значения этого коэффициента приводятся в справочниках. Заключение: мы получили схематизированную диаграмму предельных амплитуд цикла в виде прямой, которая отсекает на оси ординат
|
||||||||||||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 559; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.52.77 (0.013 с.) |

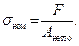
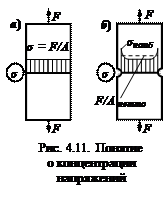 Таким образом, если деталь имеет нарушения призматической формы, то около этих нарушений имеется концентрация напряжений.
Таким образом, если деталь имеет нарушения призматической формы, то около этих нарушений имеется концентрация напряжений. Концентрация напряжений оценивается теоретическим коэффициентом концентрации напряжений – αр (α σ, α τ) – этот коэффициент называется ещё упругим коэффициентом концентрации напряжений.
Концентрация напряжений оценивается теоретическим коэффициентом концентрации напряжений – αр (α σ, α τ) – этот коэффициент называется ещё упругим коэффициентом концентрации напряжений.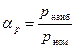 показывает, во сколько раз, местные напряжения больше номинальных, тогда р наиб =αр·р ном: αр > 1.
показывает, во сколько раз, местные напряжения больше номинальных, тогда р наиб =αр·р ном: αр > 1.
 Разрушение происходит и при
Разрушение происходит и при 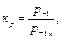
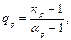
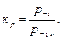
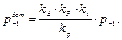
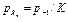 , где К – коэффициент снижения предела выносливости – это отношение предела выносливости стандартных лабораторных образцов (материала) к пределу выносливости детали, при одинаковой асимметрии цикла.
, где К – коэффициент снижения предела выносливости – это отношение предела выносливости стандартных лабораторных образцов (материала) к пределу выносливости детали, при одинаковой асимметрии цикла.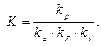

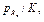 так можно получить точки для любого
так можно получить точки для любого 

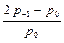 – коэффициент чувствительности материала к асимметрии цикла напряжений.
– коэффициент чувствительности материала к асимметрии цикла напряжений.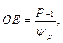
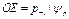 .
.


