Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчёт толстостенных цилиндровСодержание книги
Поиск на нашем сайте
8.1. Напряжения в толстостенном цилиндре,
1) Цилиндры без нормальной силы (рис. 8.2). Легко убедиться, что в этом случае нормальная сила в любом сечении цилиндра равна нулю. 2) Цилиндры с нормальной силой (рис. 8.3, а). Пример – газовый баллон – цилиндр с днищами, нагруженный внутренним давлением газа. На цилиндр действуют наружное давление р b и внутреннее давление ра. В этом случае разность сил, действующих на наружный и внутренний торцы даёт нормальную силу.
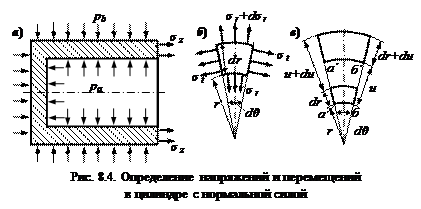
Вырежем элемент радиусом r, толщиной dr и размерами в плане dθ, dz (рис. 8.3, б). Покажем напряжения на гранях этого элемента (рис. 8.3, в). В силу осевой симметрии можно считать, что элемент после нагружения, угловых деформаций (сдвигов) не получает, то есть касательные напряжения τ по граням элемента равны нулю, то есть, эти грани являются главными. По ним действуют только нормальные напряжения – главные напряжения (приращения не показаны). σ r – радиальное напряжение, σ t – кольцевое (окружное) напряжение, σ z – осевое напряжение. Таким образом, в любой точке цилиндра, имеет место объёмное напряжённое состояние. Совершенно очевидно, что в каждой точке цилиндра, свои напряжения. Осевое напряжение не меняется, за исключением торцов, но там, есть стеснение и напряжения там, сжимающие, то есть наибольшее осевое напряжение действует в цилиндре, а не в крышке. Определим осевое напряжение. 1) Для цилиндра без нормальной силы: N = 0, σ z = N / A = 0. 2) Для цилиндра с нормальной силой (рис. 8.4, а) Составим уравнение статики
– осевое напряжение для цилиндра с нормальной силой. Получим два других компонента напряжений – здесь задача сложнее. Изобразим элемент в плоскости сечения и покажем напряжения (рис. 8.4, б). Окружное напряжение σ t от θ не зависит, так как задача осесимметричная. Изменением σ t по радиусу пренебрегаем, так как в уравнениях статики получаются величины второго порядка малости. Под действием сил, элемент находится в равновесии, поэтому
Здесь учтено, что для малого угла dθ: cos θ = 1. Далее учитываем, что sin θ / 2 = θ / 2, пренебрегая величинами второго порядка малости, сделаем преобразования и получим
– это одно из уравнений статики. Остальные пять удовлетворяются тождественно. Таким образом, статика даёт только одно уравнение, а неизвестных два, следовательно, одного уравнения не хватает (как всегда, задача о распределении напряжений по поперечному сечению, оказалась статически неопределимой). Поэтому необходимо установить закономерности деформации цилиндра. Для этого рассмотрим элемент до нагружения и после нагружения (рис. 8.4, в). После нагружения элемент не искривился, так как на его гранях нет касательных напряжений и угол элемента, не изменяется – это не закономерность, а следствие осевой симметрии. Покажем перемещения элемента u – радиальное перемещение на радиусе r, u + d u – радиальное перемещение на радиусе r + d r. Закономерность – перемещения являются непрерывными функциями координат точек цилиндра (так как в цилиндре, нет разрывов), поэтому будет u + d u – мы учли неразрывность функций. Теперь составим уравнение, выражающее закономерность деформации цилиндра – через и выразим радиальную и окружную деформации.
Исключим параметр u
– это уравнение совместности (неразрывности) деформаций, но оно записано, в относительных удлинениях. Запишем последнее уравнение, в напряжениях. По закону Гука
Подставим в уравнение совместности деформаций и учтём, что d σz / d z = 0
– уравнение совместности деформаций в напряжениях. Решая совместно уравнения (8.1) и (8.2), получим
– формулы для напряжений в толстостенном цилиндре. Строго говоря, такие напряжения будут только в средней части цилиндра, а у торцов, напряжения меньше, так как торцы стесняют деформацию, поэтому там, и деформации, и напряжения меньше. Как правило, цилиндры разрушаются в средней части, что указывает на правильность этого вывода. Проанализируем формулы. Напряжения, от z не зависят, от θ тоже (это было оговорено, выше). Видно, что в зависимости от радиуса r напряжения изменяются по закону квадратичной параболы. 8.2. Расчёт толстостенного цилиндра, Это случай, когда внешним давлением можно пренебречь. Такая расчётная схема встречается довольно часто. Например, втулка, напрессованная на вал (рис. (рис. 8.5, а-б). Если в уравнениях (8.3) принять р b = 0, то получим
Чтобы проследить за изменением напряжений по толщине стенки построим эпюры этих напряжений (рис. 8.5, в).
На внутренней стенке σ r = ра, на наружной стенке – σ r = 0. Линия между этими точками – квадратичная парабола, выпуклостью к нулевой линии. Кольцевые напряжения σ t. На наружной стенке (при r = b), σ t вычислять не будем, так как оно намного меньше ра. На внутренней стенке (при r = a), σ t даже больше, чем ра. Линия между этими точками – квадратичная парабола, тоже выпуклостью к нулевой линии. Следует отметить, что наибольшие напряжения действуют на внутренней поверхности цилиндра, то есть самыми напряжёнными являются точки на внутренней поверхности толстостенного цилиндра. Расчёты на прочность можно вести двумя методами.
|
|||||||||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 319; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.166.224 (0.007 с.) |

 К толстостенным, относятся цилиндры, толщина стенок которых сравнима с диаметром d cp < 20 h. Многие детали машин, детали двигателей летательных аппаратов могут быть отнесены к толстостенным цилиндрам. Например, втулка зубчатого колеса (рис. 8.1, а). К такой же расчётной схеме приводится ствол артиллерийского орудия (рис. 8.1, б).
К толстостенным, относятся цилиндры, толщина стенок которых сравнима с диаметром d cp < 20 h. Многие детали машин, детали двигателей летательных аппаратов могут быть отнесены к толстостенным цилиндрам. Например, втулка зубчатого колеса (рис. 8.1, а). К такой же расчётной схеме приводится ствол артиллерийского орудия (рис. 8.1, б).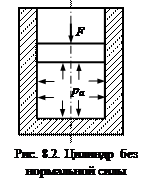 Вначале обратим внимание на то, что все цилиндры, могут быть разделены на две группы
Вначале обратим внимание на то, что все цилиндры, могут быть разделены на две группы

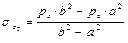
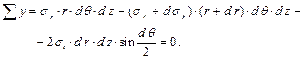
 (8.1)
(8.1)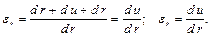
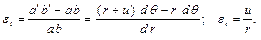
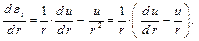
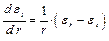


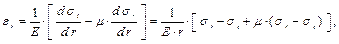 тогда
тогда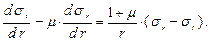 (8.2)
(8.2)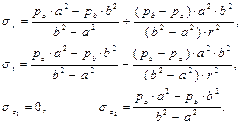 (8.3)
(8.3) (8.4)
(8.4)