
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчёт по предельным нагрузкам.
Возможности материала в этом случае занижены, но опыт показывает, что занижение, незначительно. Этот расчёт применяется тогда, когда некоторые пластические деформации не нарушают нормальной работы цилиндров. Пример. Цилиндр с жидкостью (или газом) (рис. 8.7) несколько увеличивает свои размеры, но его работоспособность не нарушается. ра ≤ ра т (рис. 8.7, а), где ра т – внутреннее давление, при котором появляются первые пластические деформации. Как его найти? Нужно эквивалентное напряжение приравнять пределу текучести σ т.При ра = При ра >
изменяемой системой. Несущая способность цилиндра исчерпана. Это давление 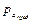 и будет опасным давлением по способу предельных нагрузок. и будет опасным давлением по способу предельных нагрузок.
Приведём готовые результаты. С ростом отношения b / a, Порядок (алгоритм) расчёта. Вначале находят ра = – формула для определения грузоподъёмности по способу предельных нагрузок. У каждого из этих двух методов расчёта имеется своя область применения. 8.3. Применение составных цилиндров Упругая грузоподъёмность – это грузоподъёмность, вычисленная по способу допускаемых напряжений. Запишем выражение для упругой грузоподъёмности
Изобразим график этой зависимости (рис. 8.9). При b / a = 1 грузоподъёмность равна нулю. Из графика видно, что грузоподъёмность можно увеличить за счёт увеличения толщины стенки, только при небольших толщинах стенки (при небольших b / a). При бóльших толщинах увеличение толщины стенки не приводит к существенному изменению грузоподъёмности.
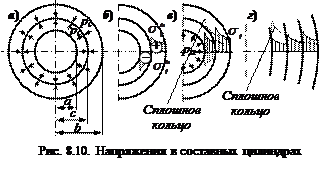
Но есть способ увеличения упругой грузоподъёмности выше [ σ ] / 2. Он основан на применении составных цилиндров (рис. 8.10), причём наружный диаметр внутреннего цилиндра больше, чем внутренний диаметр наружного цилиндра на величину ∆, где ∆ – радиальный натяг. Из двух цилиндров можно получить исходный цилиндр (рис. 8.10, а). Вес составного цилиндра будет равен весу исходного. Наружный цилиндр нагревают и надевают на внутренний и, после остывания, между ними возникает контактное давление рс (внутренний цилиндр сжимается, а наружный – растягивается), которое вызывает монтажные (начальные) напряжения. Начальные размеры цилиндров изменяются незначительно, поэтому считаем, что размеры а, b, и с неизменны. Будем рассматривать только кольцевые напряжения Проследим, как складываются эти напряжения. На рисунке 8.10, в пунктирной линией показаны напряжения для сплошного цилиндра, а также монтажные напряжения, сплошными линиями – напряжения для составного цилиндра после сложения. В точках на внутренней поверхности напряжения уменьшились существенно, следовательно, Упругая грузоподъёмность составных цилиндров увеличивается за счёт положительной роли монтажных напряжений, за счёт выравнивания напряжений по толщине стенки цилиндра и, как результат, наблюдается повышение грузоподъёмности. Можно использовать многослойные цилиндры рис. 8.10, г), тогда упругая грузоподъёмность увеличится ещё больше. Стволы артиллерийских орудий являются многослойными цилиндрами. Для расчёта составных цилиндров необходимо знать зависимость рс = рс (Δ). Получим формулу для радиального перемещения сплошного цилиндра и = и (r) (рис. 8.11, a):
Здесь σ z = 0, так как составляются открытые цилиндры,
– общая формула для радиальных перемещений. Рассмотрим картину деформаций при составлении цилиндров (рис. 8.11, б).
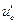 – радиальное перемещение точек внутренней поверхности наружного цилиндра, – радиальное перемещение точек внутренней поверхности наружного цилиндра,
Закономерность деформаций
∆ = Выразим перемещения, используя общую формулу. 1) Определим радиальное перемещение точек внутренней поверхности наружного цилиндра
2) Определим радиальное перемещение точек наружной поверхности внутреннего цилиндра. В этом случае параметры равны r = c, ра = 0, р a = рс, а = a, b = c.
Подставим значения перемещений в уравнение совместности деформаций
Выразим давление на стыке цилиндров
– зависимость между натягом и давлением на стыке цилиндров. Если натяг небольшой и цилиндры короткие, то их можно составить, запрессовкой. Если натяг большой и цилиндры длинные, то внешний цилиндр нагревают, и надевают, на внутренний. Вычислим, насколько нужно нагревать внешний цилиндр
В данном случае а = 0, с = 20 мм, b = 30 мм, E = 2·105 МПа. 1) Определим контактное давление
2) Построим эпюры радиальных и окружных напряжений (рис. 8.12, б)
Строим эпюры для кольца а = с = 20 мм, b = 30 мм, р a = 44,45 МПа, р b = 0. Внутренняя поверхность кольца r = c = 20 мм
Наружняя поверхность кольца r = b = 30 мм
Строим эпюры для вала а = = 0, с = b = 20 мм, ра = 0,
3) Определяем
Вопросы для самопроверки 1. Какие цилиндры называются толстостенными? 2. Какой вид напряжённого состояния испытывают точки толстостенного цилиндра? 3. Какие точки толстостенного цилиндра наиболее нагружены? 4. В чём разница расчёта на прочность толстостенного цилиндра по допускаемым напряжениям и по предельным нагрузкам? 5. Каким образом можно увеличить упругую грузоподъёмность толстостенного цилиндра? ТОНКОСТЕННЫЕ ОБОЛОЧКИ Тонкостенная оболочка – это тело (деталь), один из размеров которого, значительно меньше двух других размеров (d cp > 20 h). Меньший размер, называется толщиной оболочки. Она измеряется перпендикулярно срединной поверхности.
Примеры: паровой котёл (рис. 9.1), корпус летательного аппарата, корпус двигателя летательного аппарата. 9.1 Напряжения в осесимметричной оболочке
Изгиб возникает лишь в местах резкого изменения формы и приложения силы (рис. 9.3). Получим формулы для определения напряжений, действующих в оболочке (рис. 9.4). Выделим из оболочки элемент двумя парами меридиональных и перпендикулярных к меридиональным, поверхностями.
Ст – центр кривизны дуги меридиана срединной поверхности, ρт – радиус кривизны дуги меридиана срединной поверхности, С t – центр кривизны нормального сечения, перпендикулярного дуге меридиана, ρ t – радиус кривизны нормального сечения, перпендикулярного к дуге меридиана. Покажем элемент отдельно (рис. 9.4, б). σт – меридиональное напряжение, σ t – окружное напряжение. В силу осевой симметрии, касательные напряжения отсутствуют. Используем уравнение статики – рассмотрим сумму проекций сил на внешнюю нормаль к элементу (рис. 9.5)
В силу малости углов dθ и dφ sin dθ / 2 = dθ / 2, sin dφ / 2 = dφ / 2, и можно сократить на dθ и dφ, тогда
Поделим полученное равенство на ρт · h · ρ t и получим
– уравнение Лапласа. Возникает вопрос? В каком соотношении находятся давление р и напряжения σт и σ t? Проанализируем уравнение Лапласа. Пусть ρт = ρ t = ρ, тогда σт = σ t = σ и, следовательно,
Решая совместно (1) и (2) находим σт и σ t. 9.2. Расчёт на прочность Для сферической оболочки (рис. 9.6) ρ m = ρ t = D / 2. В силу симметрии σт = σ t = σ. Из уравнения Лапласа
На наружной поверхности – σ r = 0, а на внутренней поверхности –
Применяем третью теорию предельных напряжённых состояний
– одинаково во всех точках сферической оболочки, следовательно,
– условие прочности сферической оболочки, нагруженной внутренним давлением.
При расчёте по предельным нагрузкам получается тот же результат, так как предельные состояния по допускаемым напряжениям и по предельным нагрузкам одинаковы (в силу малости толщины).
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 269; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.79.45 (0.039 с.) |
 В этом случае, за опасное внутреннее давление принимается давление, при котором цилиндр начинает течь, то есть при котором цилиндр становится геометрически изменяемой, иначе говоря, происходит рост деформаций, при неизменном давлении (рис. 8.6).
В этом случае, за опасное внутреннее давление принимается давление, при котором цилиндр начинает течь, то есть при котором цилиндр становится геометрически изменяемой, иначе говоря, происходит рост деформаций, при неизменном давлении (рис. 8.6).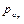 ,
, 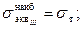
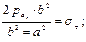
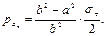

 Методами сопротивления материалов задача об определении
Методами сопротивления материалов задача об определении 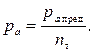
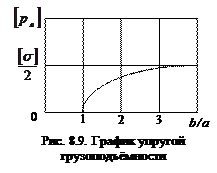

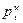 – напряжения на стыке цилиндров. Покажем эпюру монтажных напряжений (рис. 8.10, б) и суммарную эпюру (рис. 8.10, в) – рабочие напряжения складываются с монтажными.
– напряжения на стыке цилиндров. Покажем эпюру монтажных напряжений (рис. 8.10, б) и суммарную эпюру (рис. 8.10, в) – рабочие напряжения складываются с монтажными. уменьшается, а грузоподъёмность [ ра ] увеличивается и превысит [ σ ] / 2, – в этом смысл применения составных цилиндров.
уменьшается, а грузоподъёмность [ ра ] увеличивается и превысит [ σ ] / 2, – в этом смысл применения составных цилиндров.
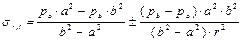 , тогда
, тогда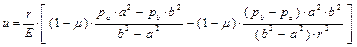

 – радиальное перемещение точек наружной поверхности внутреннего цилиндра.
– радиальное перемещение точек наружной поверхности внутреннего цилиндра. но
но 

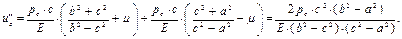
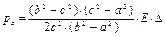
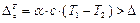 , отсюда
, отсюда 

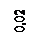
 Пример. На вал запрессовано внутреннее кольцо подшипника (рис.8.12, а) с радиальным натягом ∆ = 16 мкм = 0,016 мм. Определить контактное давление между внутренним кольцом подшипника и валом редуктора. Построить эпюры радиальных σ r и окружных σ t напряжений для кольца и вала. Определить
Пример. На вал запрессовано внутреннее кольцо подшипника (рис.8.12, а) с радиальным натягом ∆ = 16 мкм = 0,016 мм. Определить контактное давление между внутренним кольцом подшипника и валом редуктора. Построить эпюры радиальных σ r и окружных σ t напряжений для кольца и вала. Определить 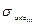 в опасной точке соединения.
в опасной точке соединения.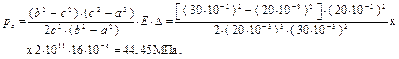
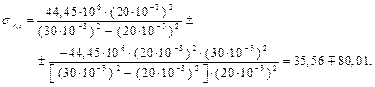


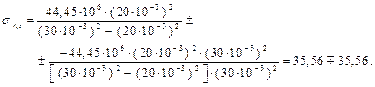
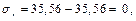

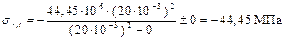 , то есть в валу, и окружные и радиальные напряжения, по радиусу постоянны.
, то есть в валу, и окружные и радиальные напряжения, по радиусу постоянны.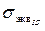 в опасной точке на внутренней поверхности кольца
в опасной точке на внутренней поверхности кольца = 115,6 + 44,45 = 160,1 МПа.
= 115,6 + 44,45 = 160,1 МПа. Срединная поверхность – это поверхность, проходящая через середины толщин оболочки. Если срединная поверхность является плоскостью, то это пластина. Если срединная поверхность – поверхность вращения, то оболочка осесимметричная. Бывают сферические, цилиндрические, конические и другие осесимметричные оболочки.
Срединная поверхность – это поверхность, проходящая через середины толщин оболочки. Если срединная поверхность является плоскостью, то это пластина. Если срединная поверхность – поверхность вращения, то оболочка осесимметричная. Бывают сферические, цилиндрические, конические и другие осесимметричные оболочки. Рассмотрим осесимметричную оболочку постоянной толщины (рис. 9.2, а). На оболочку действует внутреннее давление р. Считаем, что напряжения по толщине оболочки постоянны (рис. 9.2, б), тогда изгибающий момент отсутствует и оболочка находится в безмоментном состоянии, то есть σ = const и стенка испытывает только растяжение.
Рассмотрим осесимметричную оболочку постоянной толщины (рис. 9.2, а). На оболочку действует внутреннее давление р. Считаем, что напряжения по толщине оболочки постоянны (рис. 9.2, б), тогда изгибающий момент отсутствует и оболочка находится в безмоментном состоянии, то есть σ = const и стенка испытывает только растяжение.
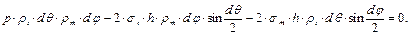

 (9.1)
(9.1)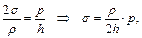 но
но  >> 1, поэтому σ >> р, или σт = σ t >> р.
>> 1, поэтому σ >> р, или σт = σ t >> р. Составим второе уравнение для определения σт, σ t, рассмотрев сумму проекций сил на ось z (рис. 9.5)
Составим второе уравнение для определения σт, σ t, рассмотрев сумму проекций сил на ось z (рис. 9.5)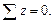 (9.2)
(9.2)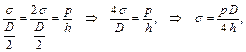
 то есть
то есть 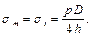
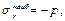 но σ t >> р, поэтому радиальными напряжениями можно пренебречь, тогда
но σ t >> р, поэтому радиальными напряжениями можно пренебречь, тогда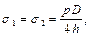 σ 3 = 0.
σ 3 = 0.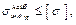 где
где 




