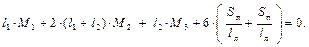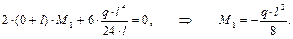Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обобщённая сила и обобщённое перемещение.
В предыдущем параграфе мы определили работу внешних сил при простых деформациях и получили (рис. 1.6).
Обобщая все три случая, можно записать
где F – обобщённая сила, ∆ – обобщённое перемещение. Обобщённая сила может быть либо силой, либо парой сил, либо какой-нибудь более сложной величиной. Обобщённое перемещение может быть либо линейным, либо угловым перемещением, либо более сложной величиной. Рассмотрим примеры: 1) Система балок нагружена группой сил F 1, F 2 и реакциями в заделках (рис. 1.7, а). Длины балок неодинаковы. Работу создают только силы, так как у реакций нет перемещений, поэтому
2) Более сложный пример. Балка на двух опорах, нагруженная распределённой нагрузкой интенсивностью (рис. 1.7, б). Имеем группу сил: реакции в опорах А, В, и распределённую нагрузку. Вычислим работу этой группы сил при статическом нагружении. Реакции опор работу не создают (нет перемещений). Рассмотрим произвольное сечение z
Здесь ω = 1.3. Взаимность работ и взаимность перемещений. В этом разделе речь пойдёт о фундаментальных положениях сопротивления материалов (теории упругости), об очень важных свойствах упругих тел. Вначале о новых обозначениях перемещений – Δ ik. Первый индекс i показывает место и направление перемещения, а второй k – силу (причину), вызвавшую это перемещение. Например, рассмотрим консольную балку, нагруженную в сечениях 1 и 2 (рис. 1.8, а). Силы приложены к недеформированной балке. Δ1 и Δ2 – полные перемещения точек при совместном действии обеих сил. Если приложить силы поочерёдно (рис. 1.8, в), то мы получаем ещё четыре перемещения. В частности, Δ21 – перемещение сечения 2 по направлению силы F 2, вызванное силой F 1. В нашем случае – это угол поворота сечения 2 от силы F 1.
В первом варианте (рис. 1.9, а) вначале приложим силу F 1 (этап I), а затем, к уже деформированной балке, приложим силу F 2 (этап II). Энергию деформации определим через работу внешних сил
На первом этапе сила F 1 достигает своего конечного значения и на втором этапе уже не меняется, поэтому во втором слагаемом, коэффициент 1/2 отсутствует. Во втором варианте (рис. 1.9, б) вначале приложим силу F 2 а затем, к уже деформированной балке, приложим силу F 1 и аналогично предыдущему вычислим энергию деформации
Приравнивая правые части и суммируя подобные произведения, получим
Разберёмся в физическом смысле полученного выражения. Левая часть Правая часть Сформулируем закономерность, именуемую взаимностью работ. Работа одной группы сил на перемещениях, вызванных другой группой сил, равна работе второй группы сил на перемещениях, вызванных первой группой сил. Здесь мы обобщили для группы сил, а при выводе рассматривали, две сосредоточенные силы. Значительно большее значение имеет следствие, а именно, взаимность перемещений. Введём понятие о единичном нагружении. Рассмотрим однопролётную балку, нагруженную сосредоточенной силой F в сечении i (рис. 1.10, а). Реакции опор A, B. Поделим нагружение на F (рис. 1.10, б)
Величины перемещений Δ ik зависят не только от жёсткости упругой системы, но и от величины сил Fk, поэтому не могут характеризовать эту систему. Перейдём к относительной величине Таким образом, податливость δ ik – это перемещение в направлении силы Fi под действием единичной силы, заменяющей силу Fk. Нагрузим балку единичными силами последовательно в сечении i (рис. 1.10, б) и k: (рис. 1.10, в). Итак, будем рассматривать две группы сил. Первая группа: Вторая группа: Применим теорему взаимности работ к этим группам:
Перемещение в сечении i от единичной силы, приложенной в сечении k, равно перемещению в сечении k от единичной силы, приложенной в сечении i. Эта закономерность называется теоремой о взаимности перемещений. Она справедлива также и для углов поворота и всех других обобщённых перемещений. 1.4. Интеграл Мора для определения При выводе формулы рассмотрим частный случай, но полученное соотношение справедливо в самом общем случае. В качестве примера возьмём балку на двух опорах, к которой приложены силы F 1 и F 2 (рис. 1.11, а). Будем рассматривать прогиб в произвольном сечении k. Наша задача вывести формулу для определения прогибов сечения k, основываясь на энергетических соображениях.
Можно определить изгибающий момент MF, а затем потенциальную энергию деформации 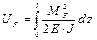 и ту же энергию можно выразить через работу внешних сил и ту же энергию можно выразить через работу внешних сил 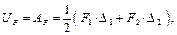 здесь множитель 1/2, так как нагружение статическое. здесь множитель 1/2, так как нагружение статическое.
Рассмотрим нагружение той же балки, единичной силой в сечении k (рис. 1.11, б) и определяем прогиб под единичной силой δ kk. И в этом случае можем вычислить изгибающий момент Ту же энергию вычислим через работу: Далее рассмотрим суммарное нагружение от заданных сил и единичной силы (рис. 1.11, в). Для суммарного нагружения можно вычислить изгибающий момент, воспользовавшись принципом суперпозиции,
Первое слагаемое полученного выражения – это энергия, накопленная балкой при нагружении внешними силами. Последнее – энергия, накопленная балкой от нагружения единичной силой. Видно, что при определении энергии принцип суперпозиции применять нельзя, так как получили три слагаемых, а не два. Итак, при суммарном нагружении:
Вычислим энергию деформации через работу действующих сил (рис. 1.11, г). Вначале прикладываем единичную силу, а затем силы F 1 и F 2.
Здесь ∆1 и ∆2 такие же, как и при отсутствии единичной силы. На втором этапе нагружения работает также и единичная сила (1·∆ k, так как она не изменяется). Тогда
Приравниваем правые части выражений
Отсюда
– интеграл Мора для определения перемещений, где ∆к – искомое перемещение – это, либо прогиб, либо угол поворота, либо другое обобщённое перемещение; MF – изгибающий момент от сил, для которых ищется перемещение;
Е· J – жёсткость балки при изгибе. Интеграл нужно вычислять по всей длине балки. Преимущества этого способа определения перемещения по сравнению с дифференциальным уравнением изогнутой оси балки: однократное интегрирование, не нужны граничные условия. Дифференциальное уравнение изогнутой оси балки применяется тогда, когда нужны закономерности изменения перемещений по всей длине балки (уравнения углов поворота и прогибов). Из формулы (1.1) можно выявить физический смысл интеграла Mора – это работа единичной силы на искомом перемещении.
Отсюда вытекает правило знаков для перемещений: если Аналогичные интегралы для определения перемещений можно получить и при центральном растяжении (сжатии), сдвиге и кручении.
Нагрузим балку единичным моментом (рис. 1.12, б). Изгибающие моменты М F = – F · z; Знак (+) означает, что сечение поворачивается по направлению единичной пары сил, то есть по ходу часовой стрелки. Интегрирование несколько затрудняет вычисление перемещений (особенно, когда много сил и участков), поэтому применяется графоаналитический способ вычисления интеграла Мора. 1.5. Графоаналитический способ вычисления Запишем интеграл Мора
Рассмотрим способ Верещагина (рис. 1.13). Обычно балки бывают постоянной жёсткости, то есть Обозначим MF = M (z). Изгибающий момент от единичного нагружения (единичная эпюра) для балок всегда линейная функция – Построим эпюры изгибающих моментов от заданных сил и единичного нагружения, тогда
Интеграл во втором слагаемом полученного выражения представляет собой площадь эпюры MF – Ω, в первом – статический момент этой площади относительно оси ординат: Sy = Ω· z c, следовательно
Обозначим
При использовании способа Верещагина, эпюры не заштриховываются, чтобы не загромождать рисунок. Пример: определить прогиб свободного конца консольной балки, нагруженной сосредоточенной силой (рис. 1.14).
1.6. Правила перемножения эпюр Правило 1. Если эпюра
Правило 2. Если эпюра М F также линейна (рис. 1.15, б), то операция перемножения обладает свойством коммутативности, то есть Ω· 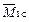 = Ω1· MFc, где Ω1 – площадь единичной эпюры; MFc – значение момента на грузовой эпюре, над центром тяжести единичной эпюры. = Ω1· MFc, где Ω1 – площадь единичной эпюры; MFc – значение момента на грузовой эпюре, над центром тяжести единичной эпюры.
Правило 3. Если эпюра MF сложная фигура (рис. 1.16, a), то её следует расслоить. Расслоить эпюру – это значит построить эпюру от каждой силы в отдельности.
Вид расслоения должен быть выбран таким, чтобы операция перемножения эпюр была как можно проще. Как правило, расслоение следует проводить к тому сечению, в котором определяется перемещение. 1.7. Формулы для площадей и положения центров тяжести Для того, чтобы воспользоваться формулой Верещагина нужно определить площадь Ω и положение центра тяжести криволинейного треугольника с основанием l и высотой h. Рассмотрим криволинейный треугольник, ограниченный осью абсцисс и одночленной параболой n -й степени у = a zn (рис. 1.17). Начнём с площади:
Окончательная формула
Вычислим статический момент площади криволинейного треугольника относительно оси ординат
– формула для положения центра тяжести криволинейного треугольника. Полученные формулы можно применять только для треугольников, ограниченных одночленной параболой при начале координат, в вершине треугольников. Для лучшего запоминания представим их в виде таблицы (рис. 1.18). Пример 1. Рассмотрим консольную балку, нагруженную равномерно распределённой нагрузкой (рис. 1.19, а). Выясним степень кривизны. Для этого помещаем начало координат в крайнее правое сечение и составляем уравнение для изгибающих моментов Пример 2. Рассмотрим консольную балку, нагруженную распределённой нагрузкой Можно ли к этому треугольнику применить наши формулы и чему равен? Составляем уравнение для изгибающих моментов.
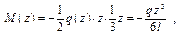 видно, что это одночленная степенная функция. Следовательно, наши формулы применять можно, видно, что это одночленная степенная функция. Следовательно, наши формулы применять можно,причём n = 3. В реальных конструкциях интенсивность может быть распределена по более сложному закону, но её можно привести к простым. Пример 3. Рассмотрим консольную балку, нагруженную распределённой нагрузкой
Чтобы применить формулу Верещагина, необходимо поступить следующим образом: 1 способ – определить реакции в опоре а и расслоить эпюры по левым силам; 2 способ – дополнить распределённую нагрузку до полной и вычесть дополненную. Расслаивать эпюры, по правым силам. Вопросы для самопроверки 1. Как записывается потенциальная энергия деформации бруса при центральном растяжении или сжатии? 2. Как записывается потенциальная энергия бруса при изгибе? 3. Как записывается потенциальная энергия бруса при кручении? 4. Что понимается под обобщённой силой? 5. Что представляет собой обобщённое перемещение? 6. Что называется податливостью? Как она определяется? 7. Как записывается интеграл Мора для определения перемещений при изгибе? 8. Каков порядок определения прогибов с помощью интеграла Мора? 9. Каков порядок определения углов поворота с помощью интеграла Мора? 10. Как записывается формула Верещагина для определения перемещений при изгибе? 11. Какие ограничения накладываются при применении способа Верещагина? 12. Каков порядок определения прогибов с помощью способа Верещагина? 12. Каков порядок определения углов поворота с помощью способа Верещагина? 13. Как производится перемножение эпюр при использовании способа Верещагина, если единичная эпюра – ломаная прямая? 13. Каким свойством можно воспользоваться при определении перемещений способом Верещагина, если и единичная и грузовая эпюра – линейные функции. 14. Как производится перемножение эпюр при использовании способа Верещагина, если грузовая эпюра – сложная фигура? 15. В чём заключается расслоение грузовых эпюр при использовании способа Верещагина? 16. Как можно проводить расслоение грузовых эпюр при использовании способа Верещагина? 2. НАИБОЛЕЕ ОБЩИЕ МЕТОДЫ РАСКРЫТИЯ Метод сил Метод сил – один из общих универсальных методов раскрытия статической неопределимости. Есть ещё метод деформаций, но он применяется при расчёте сооружений. В машиностроении при расчёте машин чаще всего применяется метод сил. Метод сил позволяет составить уравнения совместности деформаций или уравнения перемещений. Он даёт стандартный подход вне зависимости от вида конструкции.
Приступим к выводу уравнений метода сил. Рассмотрим частный случай, но уравнения получим общие. Будем рассматривать неразрезную балку (рис. 2.1, а). Неразрезной называют такую балку, которая, не прерываясь, перекрывает несколько пролётов. Эти несколько пролётов можно перекрыть и разрезными балками. Неразрезная балка имеет преимущества: у неё больше жёсткость, то есть меньше перемещения и, в большинстве случаев, больше грузоподъёмность. Недостаток – неразрезная балка – статически неопределимая балка и в ней могут быть монтажные напряжения, связанные с неточной установкой опор. Несмотря на этот недостаток, неразрезные балки широко применяются в конструкциях летательных аппаратов. В сооружениях применяются разрезные балки. Опоры нумеруются 0, 1, 2, 3, 4 (слева направо). На балку действуют активные силы и реакции опор. Неизвестных реакций шесть, а статика даёт три уравнения. Таким образом имеем три лишних неизвестных (лишних – с точки зрения статики), то есть балка три раза статически неопределима. У балки три промежуточных опоры и всегда, стёпень статической неопределимости равна числу промежуточных опор. Для решения задачи необходимо назначить лишние неизвестные. За лишние можно принять любые неизвестные, но после отбрасывания лишних неизвестных, система должна быть геометрически неизменяемой даже в малом. Примем за лишние неизвестные реакции промежуточных опор Х 1 = R 1, Х 2 = R 2, Х 3 = R 3. После назначения лишних неизвестных, изображаем основную систему (рис. 2.1, б). Основной системой (ОС) называют статически определимую и геометрически неизменяемую систему, которая получается из исходной статически неопределимой, после отбрасывания лишних связей и внешних сил. Лишние связи – связи, в которых возникают лишние неизвестные, то есть в нашем случае, лишними связями будут промежуточные опоры. Видно, что основная система – геометрически неизменяемая и статически определимая. Далее изображаем эквивалентную систему (рис. 2.1, в). Эквивалентная система (ЭС) – это основная система, нагруженная активными силами и лишними неизвестными. Реакцию 0 не показываем, так как из уравнений статики, R 0 = 0. Почему эта система называется эквивалентной? Эквивалентная система в точности воспроизводит исходную статически неопределимую систему с точки зрения сил, перемещений, деформаций и напряжений. Далее, все вопросы, будем решать с эквивалентной системой. Метод сил позволяет составить уравнение совместности деформаций. В чём заключаются закономерности деформаций изучаемой системы? Она заключается в том, что в эквивалентной системе, перемещения в направлении "лишних" связей, должны быть равны нулю. Или иначе: Х 1, Х 2, Х 3 должны быть такими, чтобы в сечениях 1, 2, 3 эквивалентной системы прогибы обращались в ноль, то есть ∆1 = 0, ∆2 = 0, ∆3 = 0. Распишем первое соотношение. Для этого рассмотрим ряд нагружений основной системы и перемещения от этих нагружений. Первое нагружение. Приложим к основной системе единичную силу (рис. 2.2, а), соответствующую первой неизвестной силе Х 1. Прогиб равен δ 11.
Следующее нагружение основной системы силой Х 1 (рис. 2.2, б). Тогда ∆11 = δ 11· Х 1. Далее изобразим основную систему и нагрузим единичной силой, соответствующей второй неизвестной силе Х 2 (рис. 2.2, в). Затем нагрузим основную систему силой Х 2 (рис. 2.2, г) и получим перемещение ∆12 = δ 12· Х 2. Теперь нагрузим основную систему в сечении 3 вначале единичной силой (рис. 2.2, д), а затем силой Х 3 (рис. 2.2, е) и получим перемещение ∆13 = δ 13· Х 3. Мы рассмотрели нагружения неизвестными силами. Остаётся рассмотреть нагружение активными силами (рис. 2.2, ж) и получить перемещение ∆1 F. Используя принцип суперпозиции, мы получаем первое из уравнений совместности деформаций. Аналогично получаем ещё два уравнения. Первый индекс у ∆ (δ) будет совпадать с номером уравнения
Мы получили основные уравнения метода сил или канонические уравнения метода сил, для три раза статически неопределимой системы. Это, по существу, уравнения совместности деформаций. Физический смысл канонических уравнений – перемещения в эквивалентной системе, по направлению лишних неизвестных равны нулю. Запишем эти уравнения в общем виде для п -раз статически неопределимой системы.
Здесь δ ik – коэффициенты канонических уравнений – это перемещения в основной системе по направлению i -й лишней связи от единичного силового фактора, соответствующего лишнему неизвестному Xk. При i = k получаем главные коэффициенты или главные податливости основной системы (податливость – перемещение от единичной силы). Если i ≠ k, то это побочные коэффициенты канонических уравнений (побочные податливости). Вспомним о взаимности перемещений (δ ik = δ ki). Иначе говоря, матрица коэффициентов канонических уравнений симметрична относительно главной диагонали. Таким образом, нужно определять не все коэффициенты канонических уравнений, а только главные коэффициенты и коэффициенты, расположенные по одну стороны от главной диагонали. Поэтому вычисление коэффициентов канонических уравнений несколько упрощается. ∆ iF – свободные члены канонических уравнений – перемещения в основной системе по направлению i -й лишней связи от всех внешних сил. Канонические уравнения метода сил применимы к любому твёрдому телу, конструкции, которую можно считать линейной, то есть подчиняющейся закону Гука. Лишними неизвестными могут быть силы, пары сил и обобщённые силы. Мы будем применять их главным образом к стержневым системам, испытывающим изгиб. В этом случае можно получить несложные уравнения для подсчёта коэффициентов (рис. 2.3, а-б).
Вспомним интеграл Мора: 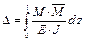 . .
Получим формулу для δ ik. Здесь
– общая формула для определения коэффициентов канонических уравнений. Аналогично получим формулу для ∆ iF. Здесь M = MF – изгибающий момент от всех внешних сил,
– формула для определения свободных членов канонических уравнений. Все моменты, в полученных формулах, вычисляются при соответствующем нагружении в основной системе. Для прямолинейных стержней коэффициенты и свободные члены канонических уравнений, можно вычислять способу Верещагина. Пример. Построить эпюры внутренних сил для заданной балки (рис. 2.4). 1) Определяем степень статической неопределимости системы: неизвестных реакций – 4, уравнений статики – 3. Система один раз статически неопределима. 2) Выбираем основную систему – за лишнюю связь принимаем реакцию шарнирной опоры. 3) Строим эквивалентную систему 4) Записываем каноническое уравнение метода сил для эквивалентной системы
5) Определяем коэффициент и свободный член канонического уравнения. Для этого последовательно нагружаем основную систему единичной силой, соответствующей Х 1, и активной силой М, строим эпюры
6) Подставляем полученные значения в каноническое уравнение и раскрываем статическую неопределимость.
7) Строим эпюры поперечных сил и изгибающих моментов в эквивалентной системе. Уравнение трёх моментов Рассмотрим неразрезную многопролётную балку (рис. 2.5, а). За лишние неизвестных при выборе основной системы удобнее принять изгибающие моменты в опорных сечениях. В этом случае основная система будет системой однопролётных балок, соединённых на опорах шарнирами. Изобразим основную систему (рис. 2.5, б), а затем эквивалентную систему (рис. 2.5, в) – она будет представлять ряд простых шарнирно-опёртых балок, нагруженных активными силами и неизвестными изгибающими моментами по концам. Рассмотрим m -ое уравнение системы канонических уравнений метода сил:
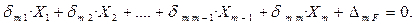
Определим коэффициенты этого уравнения по формуле
В связи с тем, что основная система представляет собой систему однопролётных балок, то в m -ом уравнении отличны от нуля будут только коэффициенты δ m m –1, δ m m,, δ m m +1. Все остальные коэффициенты обратятся в ноль, так как единичный опорный момент создаёт изгибающие моменты только в соседних пролётах АВ и ВС. Нагружаем основную систему единичными парами сил поочерёдно в сечениях m – 1, m, m + 1 (рис. 2.5, г-е) и вычисляем коэффициенты
Далее нагружаем основную систему активными силами (рис. 2.5, ж) и определяем ∆ mF по формуле
где Ω m, Ω m + 1 – площади эпюр изгибающих моментов от активных сил, приложенных к основной системе на m -ом и (m + 1)-ом пролётах, Sm, Ω m + 1 – статические моменты площадей эпюр изгибающих моментов от активных сил, приложенных к основной системе на m -ом и (m + 1)-ом пролётах. Подставим полученные значения коэффициентов в каноническое уравнение метода сил
Видно, что в полученное уравнение входят размеры и силовые факторы, относящиеся только к двум соседним пролётам АВ и ВС. Это уравнение, выражающее тот факт, что взаимный угол поворота смежных сечений пролётов АВ и ВС на m -ой опоре должен быть равен нулю. По отношению к опоре (которую будем называть средней) опора m – 1 будет левой, а опора m + 1 будет правой, соответственно и пролёты – левый и правый. Поэтому введём новые обозначения Mm –1 = M л, Mm = M ср, Mm +1 = M п, тогда
– уравнение трёх моментов. При использовании уравнения трёх моментов последовательно рассматриваются все пары соседних пролётов, причём число пар пролётов, следовательно, и уравнений, равно числу промежуточных опор, то есть степени статической неопределимости неразрезной балки. Если неразрезная балка имеет защемление или консоль (рис. 2.6, а), то в этих случаях поступают следующим образом:
При построении эпюр поперечных сил и изгибающих моментов силу F снова устанавливают в конце консоли. Теперь, о консоли. При раскрытии статической неопределимости силу F переносят на опору 3 (рис. 2.6, в), в результате получается на опоре действует пара сил М 0 = F · l 4. Сила, приложенная к опоре, имеет значение только при определении реакций опор, изгибающих моментов она не создаёт. Затем, при составлении уравнений трёх моментов для опоры 2, пару сил считают опорным моментом и тогда М п = F · l 4. При построении эпюр поперечных сил и изгибающих моментов силу F снова устанавливают в конце консоли. Пример. Построить эпюры внутренних сил для заданной балки (рис. 2.7, а). 1) Определяем степень статической неопределимости системы: неизвестных – 4, уравнений статики – 3. Система один раз статически неопределима. 2) Выбираем основную систему – заменяем заделку фиктивным пролётом l 1 = 0 (рис. 2.7, б). 3) Строим эквивалентную систему (рис. 2.7, в). 4) Записываем уравнение трёх моментов для эквивалентной системы
5) Нагружаем основную систему активной силой, строим расслоённую эпюру М F вычисляем известные величины уравнения трёх моментов (рис. 2.7, г, д). 6) В нашем случае l 1 = 0, l 2 = l, М 0 = 0, S л = 0,
7) Подставляем полученные величины в уравнение трёх моментов и раскрываем статическую неопределимость
8) Строим эпюры поперечных сил и изгибающих моментов Вопросы для самопроверки
|
|||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 253; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.53.202 (0.139 с.) |
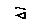
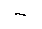

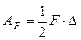 ,
,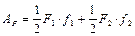 .
.
 В этом случае обобщённой силой является группа сил F 1 и F 2, а обобщённым перемещением – линейное перемещение, равное сумме прогибов балок, то есть взаимное вертикальное перемещение свободных концов балок.
В этом случае обобщённой силой является группа сил F 1 и F 2, а обобщённым перемещением – линейное перемещение, равное сумме прогибов балок, то есть взаимное вертикальное перемещение свободных концов балок.
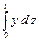 – площадь фигуры между первоначальной и изогнутой осями балки, в данном случае – обобщённое перемещение.
– площадь фигуры между первоначальной и изогнутой осями балки, в данном случае – обобщённое перемещение. Теперь вернёмся к изучению закономерностей, именуемых взаимностью работ и взаимностью перемещений. Для получения необходимых соотношений будем вычислять энергию деформации, рассматривая различные варианты статического нагружения.
Теперь вернёмся к изучению закономерностей, именуемых взаимностью работ и взаимностью перемещений. Для получения необходимых соотношений будем вычислять энергию деформации, рассматривая различные варианты статического нагружения.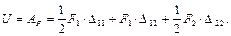

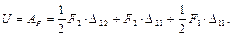

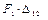 – работа силы F 1 на перемещении, вызванной силой F 2;
– работа силы F 1 на перемещении, вызванной силой F 2; – работа силы F 2 на перемещении, вызванной силой F 1.
– работа силы F 2 на перемещении, вызванной силой F 1.

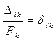 , которая называется податливостью упругой системы.
, которая называется податливостью упругой системы. ; 1 (в сечении i);
; 1 (в сечении i);  .
.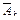 ; 1 (в сечении k);
; 1 (в сечении k); 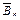 .
.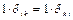 (реакции опор работу не совершают, так как нет перемещений). Тогда имеем
(реакции опор работу не совершают, так как нет перемещений). Тогда имеем

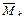 , а затем потенциальную энергию
, а затем потенциальную энергию 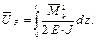
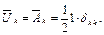
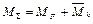 и энергию деформации
и энергию деформации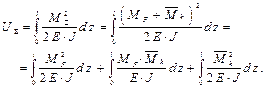

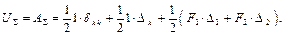
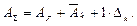
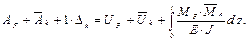
 (1.1)
(1.1)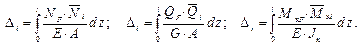
 Рассмотрим пример: определить угол поворота свободного конца консольной балки, нагруженной сосредоточенной силой (рис. 1.12, а).
Рассмотрим пример: определить угол поворота свободного конца консольной балки, нагруженной сосредоточенной силой (рис. 1.12, а).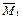 = – 1. Далее подставим полученные значения моментов в интеграл Мора и вычислим перемещение
= – 1. Далее подставим полученные значения моментов в интеграл Мора и вычислим перемещение – окончательный результат.
– окончательный результат.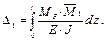
 В 20-х годах XX века русский механик А.Н. Верещагин предложил графоаналитический метод вычисления интеграла Мора. Способ Верещагина значительно повысил эффективность интеграла Мора при вычислении перемещений.
В 20-х годах XX века русский механик А.Н. Верещагин предложил графоаналитический метод вычисления интеграла Мора. Способ Верещагина значительно повысил эффективность интеграла Мора при вычислении перемещений.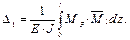
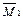 = a · z + b.
= a · z + b.
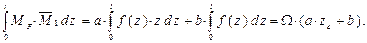
 = a · z c + b, что представляет собой ординату единичной эпюры под центром тяжести эпюры MF. Таким образом, формула Верещагина имеет вид
= a · z c + b, что представляет собой ординату единичной эпюры под центром тяжести эпюры MF. Таким образом, формула Верещагина имеет вид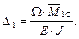
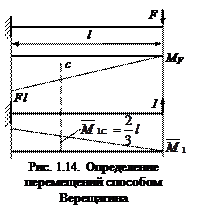 Здесь: Ω – площадь эпюры моментов от заданных сил, для которых ищется перемещение, или площадь грузовой эпюры;
Здесь: Ω – площадь эпюры моментов от заданных сил, для которых ищется перемещение, или площадь грузовой эпюры;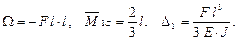
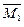 – ломаная прямая (рис. 1.15, а) (чаще всего так и бывает), то эпюры М F и
– ломаная прямая (рис. 1.15, а) (чаще всего так и бывает), то эпюры М F и 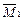 следует разбить на несколько участков, перемножение вести по каждому участку в отдельности, а результаты сложить
следует разбить на несколько участков, перемножение вести по каждому участку в отдельности, а результаты сложить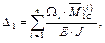
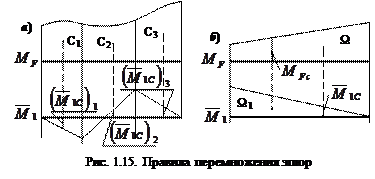
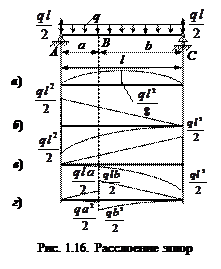 Цель расслоения – построить эпюру MF как сумму простых фигур, для которых можно легко определить площади и положение центров тяжести. Расслоение эпюр можно вести как по правым (рис. 1.16, б), так и по левым (рис. 1.16, в) силам; можно также вести смешанное расслоение (рис. 1.16, г) к одному из промежуточных сечений.
Цель расслоения – построить эпюру MF как сумму простых фигур, для которых можно легко определить площади и положение центров тяжести. Расслоение эпюр можно вести как по правым (рис. 1.16, б), так и по левым (рис. 1.16, в) силам; можно также вести смешанное расслоение (рис. 1.16, г) к одному из промежуточных сечений.
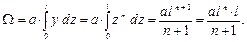
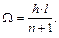
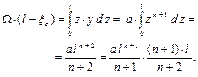
 преобразуя, получим
преобразуя, получим 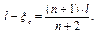 Тогда
Тогда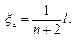
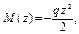 следовательно, n = 2.
следовательно, n = 2.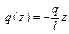 (рис. 1.19, б). Построим эпюру изгибающих моментов.
(рис. 1.19, б). Построим эпюру изгибающих моментов.
 (рис. 1.19, в). Без промежуточных вычислений запишем уравнение для изгибающих моментов.
(рис. 1.19, в). Без промежуточных вычислений запишем уравнение для изгибающих моментов. можно видеть, что к этому треугольнику формулы не применимы.
можно видеть, что к этому треугольнику формулы не применимы.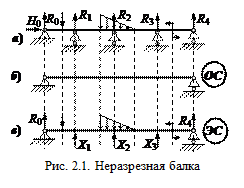

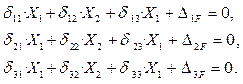
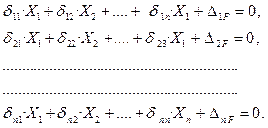
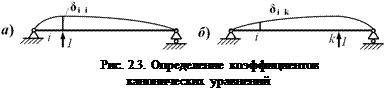
 – изгибающий момент от единичного силового фактора, соответствующего лишней неизвестной Xk,
– изгибающий момент от единичного силового фактора, соответствующего лишней неизвестной Xk,  – изгибающий момент от единичного силового фактора, соответствующего лишней неизвестной Xi, тогда
– изгибающий момент от единичного силового фактора, соответствующего лишней неизвестной Xi, тогда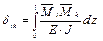 .
.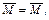 . Подставив в интеграл Мора. получим.
. Подставив в интеграл Мора. получим.
 δ 11· Х 1 + ∆1 F = 0.
δ 11· Х 1 + ∆1 F = 0.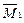 и MF. Используем способ Верещагина
и MF. Используем способ Верещагина
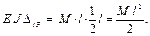
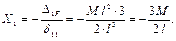

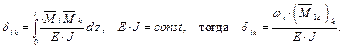

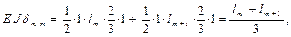
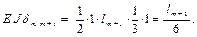
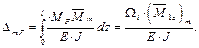
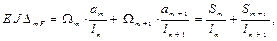
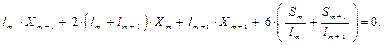
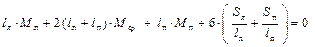
 Вместо заделки вводят две бесконечно близкие шарнирные опоры (рис. 2.6, б) (0 и 1), далее составляют уравнение трёх моментов, принимая М 0 = 0 и l 0 = 0. Теперь, о консоли. При раскрытии статической неопределимости силу F переносят на опору 3 (рис. 2.6, в), в результате получается на опоре действует пара сил М 0 = F · l 4. Сила, приложенная к опоре, имеет значение только при определении реакций опрор, изгибающих моментов она не создаёт. Затем, при составлении уравнений трёх моментов для опоры 2, пару сил считают опорным моментом и тогда М п = F · l 4.
Вместо заделки вводят две бесконечно близкие шарнирные опоры (рис. 2.6, б) (0 и 1), далее составляют уравнение трёх моментов, принимая М 0 = 0 и l 0 = 0. Теперь, о консоли. При раскрытии статической неопределимости силу F переносят на опору 3 (рис. 2.6, в), в результате получается на опоре действует пара сил М 0 = F · l 4. Сила, приложенная к опоре, имеет значение только при определении реакций опрор, изгибающих моментов она не создаёт. Затем, при составлении уравнений трёх моментов для опоры 2, пару сил считают опорным моментом и тогда М п = F · l 4.