Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Перемещения при косом изгибе
Как найти перемещения в общем случае, когда угол φ меняется по длине бруса (балки). В общем случае нагрузки, действующие на балку, раскладываются на составляющие в главных плоскостях жёсткости. Затем находится перемещение от каждой группы составляющих – каждая группа вызывает плоский изгиб. Потом эти перемещения складываются – это будет геометрическая сумма. Дело упрощается тем, что речь идёт о взаимно перпендикулярных перемещениях. Далее рассмотрим частный случай, когда положение плоскости полного изгибающего момента по длине балки не изменяется. Рассмотрим консольную балку (рис. 3.21):
Покажем составляющие силы F и перемещения f в главных плоскостях жёсткости. Для вычисления fx и fy воспользуемся готовым решением задачи при плоском изгибе – 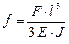 . Здесь J – момент инерции поперечного сечения относительно нейтральной оси. . Здесь J – момент инерции поперечного сечения относительно нейтральной оси.
Применим эту формулу для составляющих
Найдем положение плоскости, в которой происходит полное перемещение.
Таким образом, при повороте плоскости полного изгибающего момента от плоскости наибольшей жёсткости нейтральная ось и плоскости полного прогиба поворачиваются на одинаковый угол α, иначе говоря, плоскость полного прогиба перпендикулярна нейтральной оси. Покажем на рис. 3.21, нейтральную ось. 3.4 Внецентренное растяжение и сжатие Короткие стержни – это стержни малой гибкости. Теория, которая будет изложена ниже, применима к коротким стержням. Брус испытывает внецентренное растяжение или сжатие, если он нагружен силами, линия действия которых параллельна оси стержня, но не совпадает с ней.
bF (xF, yF) – точка приложения силы, е – эксцентриситет (расстояние от точки bF приложения силы до центра тяжести сечения С). Изобразим расчётную схему бруса (рис. 3.22, б). Переносим силы F на ось бруса, но при этом, мы должны добавить пары сил. Силы F вызывают центральное растяжение (или сжатие), а пары сил М = F · l – чистый косой изгиб. Таким образом, внецентренное растяжение или сжатие есть сумма центрального растяжения или сжатия и чистого косого изгиба, иначе: внецентренное растяжение или сжатие есть сумма центрального растяжения или сжатия и двух плоских чистых изгибов в главных плоскостях жёсткости.
Выведем формулы для напряжений в поперечном сечении бруса. Применим метод сечений, отброшенная часть показана штриховыми линиями (рис. 3.23). Покажем главные центральные оси x, y поперечного сечения.
Воспользуемся принципом суперпозиции
Подставим значения слагаемых в исходную формулу
Здесь знаки «±», чтобы охватить, и растяжение, и сжатие. Знак «+» берём при растяжении, а знак «–» – при сжатии. xF, yF – координаты (в главных) точки x, y – координаты точки, в которой вычисляют напряжение. А – площадь поперечного сечения бруса. Jx, Jy – главные центральные моменты инерции сечения бруса. Запишем формулу в другом виде: так как
Если сила приложена центрально, то xF = yF = 0 и Далее необходимо составить условие прочности. Для этого нужно найти точку с самым большим напряжением. При каждой простой деформации поперечное сечение остается плоским и поворачивается относительно нейтральной оси. Пусть x 0, y 0– координаты точек нейтральной оси, тогда
Это уравнение нейтральной оси. Координаты x 0, y 0входят в числитель в первой степени, следовательно, это уравнение прямой. Нейтральная ось не проходит через начало координат, поэтому удобно найти отрезки, которые она отсечёт от осей. Запишем уравнение нейтральной оси в отрезках
где
Так как в правой части х и у со знаком «-», то точка приложения силы и нейтральная ось всегда расположены по разные стороны от начала координат. Зная положение нейтральной оси, можно найти точку с наибольшим напряжением. Самой напряжённой будет точка, наиболее удалённая от нейтральной оси. Необходимо провести касательные к контуру сечения, параллельные нейтральной оси и найти координаты наиболее удалённой точки – это точка 1 (х 1, у 1).
Подставим в общее уравнение
– условие прочности при внецентренном растяжении или сжатии. Как пользоваться условием прочности? Вначале нужно найти положение нейтральной оси, нанести её, провести касательные, найти наиболее удалённую точку и посмотреть, выполняется ли условие прочности. Рассмотрим частный случай, когда поперечное сечение имеет две оси симметрии и выступающие острые углы, например, прямоугольник или двутавр (см. рис. 3.20). Самый удаленный всегда будет одна из угловых точек: | х 1| = | х 2| = | х 3| = | х 4| = | х | наиб; | у 1| = | у 2| = | у 3| = | у 4| = | у | наиб. Если ещё учесть, что
это частная формула. Возвращаемся к формулам для ах и ау. Если х f, у f возрастают, то, в соответствии с формулами, модули | ах | и | ау | убывают. Иначе: если точка приложения силы удаляется от начала координат, то нейтральная ось приближается к началу координат, и наоборот, если сила приближается к началу координат, то нейтральная ось удаляется от центра тяжести сечения. Если силу F удалять от начала координат, то нейтральная ось будет пересекать сечение и в пределах сечения в одной его части будет растяжение, в другой – сжатие. В строительном деле, в строительных концепциях очень важно, чтобы всё сечение испытывало только сжатие, то есть сила должна очень близко располагаться к началу координат. В связи с этим возникает понятие ядра сечения. Ядром сечения называется область сечения, включающая центр тяжести, приложение силы внутри которой вызывает во всем сечении напряжения одного знака. Таким образом, если сила приложена внутри ядра сечения, то нейтральная ось не пересекает сечение. Если сила приложена на границе ядра сечения, то нейтральная ось касается сечения – это обстоятельство используется при отыскании координат ядра сечения.
Примеры (рис. 3.25): Кручение с изгибом В чистом виде кручение встречается редко. Обычно кручение осложнено изгибом, причём изгиб возникает при передаче крутящего момента на вал. Будем изучать кручение с изгибом брусьев круглого сечения, так как подавляющее большинство деталей машин, испытывающих эту деформацию, являются брусьями круглого поперечного сечения.
Теорию изложим на частном примере (рис. 3.26, а). На вал, защемлённый одним концом, передаётся пара сил через рычаг длиной а. Изобразим расчётную схему вала (рис. 3.26, б). Вместо вала рассмотрим его ось, перенесём силу F к центру тяжести сечения вала – в результате получим силу F и пару сил М = F ·а. Сила F вызывает изгиб, а пара сил М – кручение. Следовательно, вал испытывает кручение с изгибом. Расчётная схема бруса есть, сила F и пара сил М = F ·а известны. Далее переходим к внутренним силам (рис. 3.27). Вначале анализируем изгиб – касательные напряжения от поперечной силы рассматривать не будем, так как их роль невелика. Будем рассматривать только нормальные напряжения и, следовательно, изгибающий момент Ми. Строим эпюру Ми = F · z – при этом момент берётся по абсолютной величине, а ординаты откладываются на сжатых
Теперь обратимся к теории предельных напряжений состояний. Валы, как правило, стальные. Сталь – пластичный металл и поэтому применяем четвёртую теорию – теорию октаэдрических касательных напряжений
– условие прочности по четвёртой теории в самой опасной точке сечения. Эту формулу мы выводили при изучении темы "Изгиб". Выразим σ наиб и τ наиб через М и и М к:
где W и– момент сопротивления сечения при изгибе; Для круглого сечения W к – момент сопротивления сечения при кручении. Для круглого сечения Подставляем в формулу для эквивалентных напряжений:
Теперь можем записать условие прочности через
– условие прочности в любом поперечном сечении вала. Записано оно в форме условия прочности при изгибе, но в качестве изгибающего момента записан эквивалентный момент, который учитывает и изгиб, и кручение. А нам нужно записать условие прочности для всего вала. Для этого нужно найти опасное сечение – сечение, где действует
– условие прочности всего вала круглого поперечного сечения при кручении с изгибом. Чтобы воспользоваться этим условием необходимо знать Далее рассмотрим, как решаются три задачи сопротивления материалов при кручении с изгибом? В этом случае все задачи решаются просто, как при плоском изгибе 1 задача – проверка прочности
2 задача – назначение размеров поперечного сечения. Определяем диаметр вала:
3 задача – определение грузоподъёмности.
Приведем формулы для Мэкв по другим теориям прочности:
В целом ряде случаев кроме кручения и изгиба, есть ещё растяжение или сжатие. Возникает вопрос: как при такой сложной деформации оценить прочность вала? В этом случае используется начальная формула
Тогда при вычислении σ наибнеобходимо учесть растяжение-сжатие следующим образом:
Это в любом сечении. А как поступить, для всего вала? Нужно найти сечение где действует Вопросы для самопроверки 1. Какие внутренние усилия возникают в брусе в общем случае сложного сопротивления? 2. Какие напряжения возникают в брусе в общем случае сложного сопротивления? 3. Как определяются нормальные напряжения в брусе в общем случае сложного сопротивления? 4. Как определяются касательные напряжения в брусе в общем случае сложного сопротивления? 5. Какое напряжённое состояние имеет место в точках бруса, в общем случае сложного сопротивления? 6. Как записывается условие прочности бруса в общем случае сложного сопротивления? 7. Как определяют перемещения бруса в общем случае сложного сопротивления? 8. Какие рамы называют плоскими, плоско-пространственными, пространственными? Какие внутренние усилия возникают в плоских рамах? 9. Чему численно равна нормальная сила в поперечном сечении плоской рамы? Правило знаков для нормальной силы. 10. Чему численно равна поперечная сила в сечении плоской рамы? Правило знаков для поперечной силы. 11. Чему численно равен изгибающий момент в поперечном сечении плоской рамы? Правило знаков для изгибающего момента. 12. Какие напряжения возникают в поперечном сечении плоской рамы? Как они вычисляются? 13. Как записываются условие прочности для плоской рамы? 14. Каков порядок подбор размера поперечного сечения для плоской рамы? 15. В каком случае брус испытывает косой изгиб? 16. Какие внутренние усилия возникают в брусе, испытывающем косой изгиб? 17. Какие напряжения возникают в брусе при косом изгибе и как их определяют? 18. В каком месте поперечного сечения бруса находится опасная точка при косом изгибе и как она находится? 19. Как определяется положение нейтральной оси бруса при косом изгибе? 20. Как записывается условие прочности бруса при косом изгибе? 21. Каков порядок расчёта на прочность бруса при косом изгибе; 22. Как определяются перемещения бруса при косом изгибе? 23. В каком случае брус испытывает внецентренное растяжение или сжатие (ВЦРС)? 24. Какие внутренние усилия возникают в брусе, испытывающем ВЦРС? 25. На какие простые деформации можно разложить ВЦРС? 26. Какие напряжения возникают в поперечном сечении бруса, испытывающего ВЦРС, и как их определяют? 27. В каком месте поперечного сечения бруса, испытывающего ВЦРС, располагаются опасная точка, и как она находится? 28. Как определяется положение нейтральной оси поперечного сечения бруса, испытывающего ВЦРС? 29. Как записывается условие прочности бруса, испытывающего ВЦРС? 30. Каков порядок расчёта на прочность бруса, испытывающего ВЦРС? 31. Каков порядок расчёта на прочность бруса, испытывающего ВЦРС, и имеющего две оса симметрии и прямые выступающие острые углы? 32. Каков порядок расчёта круглых валов, испытывающих кручение с изгибом? 33. Какие напряжения возникают в поперечном сечении круглого вала, испытывающего кручение с изгибом? 34. Как записывается условие прочности круглого вала, испытывающего кручение с изгибом?
4. ПРОЧНОСТЬ ПРИ ЦИКЛИЧЕСКИ Основные понятия об усталостном разрушении Достаточно большая группа деталей работает при постоянных напряжениях, особенно, в сооружениях. Детали машин испытывают, как правило, переменные напряжения. Например, шатун испытывает переменные напряжения растяжения (сжатия), лопатки турбины совершают вынужденные колебания и в них действуют переменные напряжения. Переменным напряжениям детали сопротивляются иначе, нежели постоянным. Отметим три особенности сопротивления переменным напряжениям: 1 Переменным напряжениям детали сопротивляются хуже, чем постоянным. Под действием переменных напряжений разрушение происходит при меньших напряжениях, чем при постоянных. Прочность снижается в несколько раз, в зависимости от формы и состояния поверхности деталей. 2 Разрушение наступает не сразу, а после наработки определённого числа циклов. При больших напряжениях разрушение наступает быстро, при меньших – через некоторый промежуток времени: через год, два и так далее. 3 Разрушение от переменных напряжений, даже деталей из пластичных материалов, происходит хрупко, без остаточных деформаций (нет никаких шеек). Это всё, главные особенности. Их нужно объяснить. Как объясняли их, в XIX веке? Считали, что при действии переменных напряжений, материал устаёт, снижается предел прочности σ в и снижается пластичность. Снижаясь, σ в достигает фактических значений напряжений в детали и в этот момент, происходит разрушение. Однако, в начале XX века, были поставлены опыты, которые показали, что материал, вовсе не устаёт. Вырезали из деталей образцы и оказалось, что σ в не изменяется. Никакой усталости в первоначальном понимании нет, однако термин «усталость», остался. Далее приведём современное объяснение, которое подтверждено многочисленными исследованиями. В детали, всегда есть микродефекты (микротрещины). По границам микротрещин, наблюдается концентрация напряжений и, в результате, возникают напряжения, превышающие предел текучести σ т. Общее напряжение по сечению меньше σ т, а местные напряжения, на границах микротрещин – больше σ т. Покажем это, на диаграмме напряжений (рис. 4.1). Точка 1, соответствует деформации на границе микротрещины в момент достижения напряжениями наибольшего значения при первом полуцикле нагружения. Точка 2, соответствует окончанию третьего полуцикла и так далее. Таким образом, на границе микротрещины происходит накопление пластических деформаций. Бесконечно, это накопление продолжаться не может – через определённое число циклов достигается конец диаграммы и происходит местное разрушение. В результате, размеры микротрещины несколько увеличиваются. Если напряжения небольшие, то этого, может и не произойти.
Далее, всё начинается сначала. Микротрещины растут, объединяются и после большого числа циклов, появляются макротрещины, размеры которых сопоставимы с размерами поперечного сечения детали. Макротрещина растёт, ослабляет поперечное сечение детали. В конце концов, оно будет ослаблено настолько, что фактические напряжения, достигнут предела прочности материала σ в и произойдёт разрушение. Почему разрушение носит хрупкий характер? Так как на границе трещин возникает объёмное напряжённое состояние – всестороннее растяжение – касательные напряжения малы, поэтому остаточные (пластические) деформации малы и разрушение будет хрупким. Микротрещины образуются, и в бездефектном состоянии материала. Некоторые зёрна материала, оказываются перегруженными (как в статически неопределимой системе) и при действии напряжений, возникают микротрещины. Это, современное представление. Никакой усталости, в первоначальном понимании, нет, но термин «усталость», сохранился. Усталость – процесс постепенного накопления повреждений материала под действием переменных напряжений, приводящий к образованию трещин, их развитию и разрушению. Сопротивление усталости – свойство материала противостоять усталости (сопротивление переменному напряжению, развитию трещин).
Поверхность первой зоны мелкозернистая, гладкая, видны следы фронта трещины – это зона развития макротрещины. Она гладкая, блестящая, так как поверхности прижимаются друг к другу и притираются. Там наблюдаются ступеньки и всегда видно, где зарождается трещина. Поверхность второй зоны, крупнозернистая, характерная для хрупкого разрушения. Это, та часть сечения, по которой произошло мгновенное и окончательное разрушение. Таким образом, вид разрушения, подтверждает современное объяснение особенностей сопротивления детали переменным напряжениям. Чтобы произошло усталостное разрушение, одной перемены напряжений недостаточно. Напряжения должны быть достаточно большими. Мы пришли к новому понятию – предел выносливости. Пределом выносливости называется наибольшее по абсолютному значению напряжение цикла, при котором ещё не происходит усталостное разрушение до базы испытаний. Предел выносливости обозначается через р r, при изгибе – σ r, при кручении – τ r, при растяжении-сжатии – σ r р. База испытаний N б – предварительно задаваемая наибольшая продолжительность испытаний на усталость. Предел ограниченной выносливости – наибольшее по абсолютному значению напряжение цикла, соответствующее задаваемой циклической долговечности. Обозначается Предел выносливости детали зависит от большого числа факторов (до 10), однако, на предел выносливости самого материала в основном оказывают влияние три фактора: • сам материал; • тип деформации (могут быть: растяжение (сжатие), кручение, изгиб); • соотношение, крайних за цикл, значений напряжений. В заключении запишем условие прочности для материала при действии переменных напряжений:
здесь условие прочности записано в общем виде, п r – коэффициент запаса по усталости. Параметры цикла напряжений
Изобразим график изменения напряжений с течением времени (рис. 4.3). Чаще всего детали испытывают напряжения, изменяющиеся по закону простой гармоники, но это не всегда. Закон изменения может быть и более сложным. Оказывается, что на предел выносливости, форма кривой влияния, не оказывает. На долговечность – оказывает некоторое влияние. Рассмотрим основные параметры цикла напряжений: р тах – максимальное напряжение цикла – алгебраически наибольшее напряжение цикла; р min – минимальное напряжение цикла – алгебраически наименьшее напряжение цикла;
1 Постоянные во времени напряжения (рис. 4.4, а). Это статическое нагружение. Здесь: р m ах = р min = р m = р, р a = 0, 2 Отнулевой цикл (положительный) цикл (рис. 4.4, б). Такой цикл испытывает например, шатун двигателя. Здесь: р mах = р, р min = 0, р m = р a = р/ 2, Rp = 0. У отнулевого отрицательного цикла р mах = 0, р min = р, р a = р/ 2, р m = – р/ 2, 3. Симметричный цикл (рис. 4.4, в). Такой цикл испытывают многие детали машин. Здесь: р mах = – р min = р a = р, р m = 0, Rp = – 1. При одинаковом наибольшем по абсолютной величине напряжении за цикл – симметричный цикл самый тяжёлый. Предел выносливости при симметричном цикле всегда наименьший. Как обозначаются пределы выносливости? Они встречаются в справочниках: σ –1 – предел выносливости при изгибе в случае симметричного цикла; σ – 1р – предел выносливости при растяжении/сжатии в случае симметрчного цикла; σ 0 – предел выносливости при изгибе в случае положительного отнулевого цикла; σ 0р – предел выносливости при растяжении-сжатии в случае положительного отнулевого цикла; τ – 1 – предел выносливости при кручении в случае симметричного цикла; σ – 0,3 – предел выносливости при изгибе в случае асимметричного цикла с коэффициентом асимметрии R = – 0,3 и так далее. 4.2. Предел выносливости материала Различают предел выносливости материала и предел выносливости детали. Они, разные. Рассмотрим предел выносливости материала. За предел выносливости материала условно принимается предел выносливости стандартных лабораторных образцов. Размеры этих образцов и качество изготовления оговорено в ГОСТе на усталостные испытания Образцы имеют следующие формы: цилиндрические образцы, корсетные образцы, плоские образцы и так далее. У лабораторных образцов поверхность рабочей части тщательно
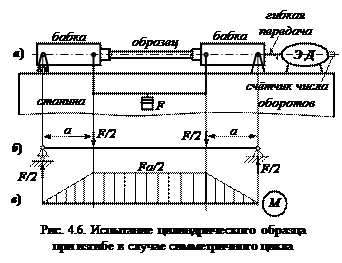
Предел выносливости материала определяется только экспериментальным путём. Для испытания цилиндрических образцов имеются специальные машины: МУИ-6000, МВП-10000 – это основные машины. Цифра в марках машин – число циклов нагружения в минуту. Познакомимся с определением предела выносливости материала при изгибе, в случае симметричного цикла, на примере цилиндрических образцов (рис. 4.5). Рассмотрим конструкцию машины (рис. 4.6, а).
В бабках – цанговые зажимы в подшипниках. В зажимах закрепляется образец. Вращение образца осуществляется от электродвигателя через гибкую передачу. На электродвигателе имеется счётчик числа циклов нагружения. F – сила веса сменных грузов. Нагрузка неподвижна, а образец вращается. После разрушения образца, электродвигатель автоматически останавливается. Изобразим расчётную схему образца (рис. 4.6, б) и построим эпюру изгибающих моментов (рис. 4.6, в). В пределах образца, изгибающий момент не изменяется. Он изменяется, только в пределах бабок – следовательно, образец испытывает чистый изгиб. Наибольший изгибающий момент равен Так можно вычислить наибольшее напряжение, которое испытывает образец. Его можно изменять, меняя вес груза. Как изменяется напряжение в одной из точек на поверхности? Полный цикл изменения напряжений происходит за один оборот образца (рис. 4.7). В опасной точке напряжение изменяется по симметричному циклу.
Испытания. Испытывают партию из 15 образцов. Нагрузку для испытаний первого образца берут такую, чтобы: 1) σ 1 = 0,6 σ в – при таком напряжении, он обязательно разрушится через N 1 циклов нагружения, после этого, ставят второй образец; 2) σ 2 < σ 1 - разрушение произойдет при большем числе циклов 3) σ 3 < σ 2 – разрушение произойдёт через N 3 > N 2. Наконец, на каком-то образце, достигнем уровня напряжения, при котором разрушение не наблюдается до базы испытаний N б. При этом напряжении, которое принимается за предел выносливости, испытывают ещё 1-2 образца. Полученные результаты представляют графически (рис. 4.8, а):
На графике нужно бы указать σ наиб, но при испытаниях рассматривается только это напряжение, поэтому оно обозначается просто σ. Для чёрных металлов N б = 107 циклов, а для лёгких сплавов и других металлов N б = 108 циклов нагружения. По ГОСТу кривые усталости строят в полулогарифмических (рис. 4.8, б) или двойных логарифмических координатах. В связи с большим рассеянием долговечности, проводятся массовые испытания. На каждом из 4-6 уровней напряжений, испытываются не менее 10 образцов, а результаты испытаний, обрабатываются методами математической статистики. В настоящее время, накоплен большой экспериментальный материал, который приводится в справочниках. Обобщение этого материала, привело к следующим эмпирическим формулам: σ –1 ≈ 0,46· σ в – среднее значение (по И.В. Кудрявцеву); σ –1р ≈ 0, 28· σ в – так как при растяжении-сжатии наибольшее напряжение действует по всему сечению образца; τ –1 ≈ 0,27· σ в. Все эти соотношения, справедливы только для сталей. Для цветных металлов нет надёжных, твёрдых соотношений, так как их пределы выносливости, изменяются в более широких пределах. 4.3. Предел выносливости материала Известно, что за предел выносливости материала условно принимают предел выносливости стандартных лабораторных образцов с тщательно полированной поверхностью рабочей части. И в рассматриваемом случае, предел выносливости определяется опытным путём, на специальных машинах, в конструкции которых предусмотрена возможность создания в образце средних напряжений цикла. Напишем параметры цикла напряжений: pm ах, pmin, pm, pa, R. Теперь рассмотрим так называемый предельный цикл. Предельным циклом напряжений называется цикл, наибольшее по абсолютной величине напря жение которого, равно пределу Обозначение параметров предельного цикла: pRm ах, pRmin, pRm, pRa, R. А чему равен предел выносливости? pR = p Rm + pRa – это наибольшее по абсолютной величине напряжение цикла. Для расчёта на прочность при переменных напряжениях нужно знать, как зависит предел выносливости от асимметрии цикла? Эту зависимость снимают опытным путём и представляют в неявном виде с помощью одной или двух диаграмм: 1. pRm ах, pRmin = f (pRm) – здесь, две кривые, 2. pR а = f (pRm) – здесь одна кривая. Для вывода расчётных формул, удобна вторая диаграмма, поэтому её и будем рассматривать. Две точки, через которые проходит кривая, нам известны заранее (рис. 4.9):
2) при pRm = p в pR а = 0, то есть разрушение происходит без переменной составляющей (статическое нагружение). Далее – промежуточные точки. Для получения каждой промежуточной точки нужно испытывать партию стандартных лабораторных образцов. В пределах партии, среднее напряжение постоянно, а изменяется, только переменная составляющая (амплитуда). Методика испытаний такая же, как и при симметричном цикле. Такие испытания проводились и опыт-ные точки ложатся следующим образом (см. график на рис. 4.9). Полученную кривую называют диаграммой предельных амплитуд цикла. Обращаем внимание: чем больше среднее напряжение, тем меньше предельная амплитуда. Для пластичных, низкопрочных материалов диаграмма предельных амплитуд цикла – выпуклая вверх кривая. Для высокопрочных – почти прямая. Обратим внимание: диаграмма построена только в области положительных средних напряжений. А как ведёт себя зависимость при отрицательных средних напряжениях? Эта область изучена ещё недостаточно, экспериментальных данных мало и они, порой, противоречивы. Академик С. В. Серенсен предлагал, чтобы слева, на небольшом участке, рассматривать диаграмму в виде прямой, параллельной оси pm. Возникает вопрос, как с помощью этой диаграммы, зная коэффициент асимметрии цикла (R), найти предел выносливости pR? Любому циклу на диаграмме соответствует точка, например, циклу с параметрами pm, pa, соответствует точка M. Если точка лежит ниже предельной кривой, то она соответствует неразрушающему циклу, но не безопасному, так как неизвестен коэффициент запаса. Если точка – выше предельной кривой, то разрушающему циклу. Если точка на предельной кривой – предельному циклу.
Из начала координат о, через точку М, проведём прямую и отметим точку пересечения с предельной кривой MR. Определим параметры предельного цикла напряжений pRm, pRa и выразим через них
Теперь ясно, как найти предел выносливости, зная R. Находим р R = р Rm +р Ra . Обращаем внимание на то, что точки, соответствующие циклу с одинаковым коэффициентом R, лежат на одной прямой, проходящей через начало координат. Почему? Так как tg β будет одинаковым. Циклы напряжений с одинаковыми коэффициентами асимметрии R называются подобными.
|
|||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 230; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.25.74 (0.159 с.) |

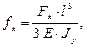
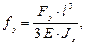
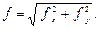
 но
но 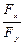 = tg φ, следовательно
= tg φ, следовательно  тогда, ψ = α.
тогда, ψ = α. Изобразим брус, испытывающий внецентренное растяжение
Изобразим брус, испытывающий внецентренное растяжение 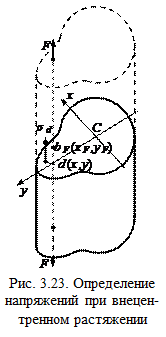 Пусть точка приложения сил
Пусть точка приложения сил 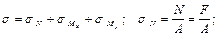
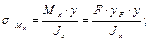

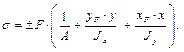

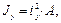 то
то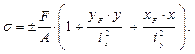
 .
.
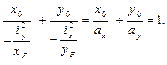
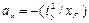 ;
; 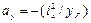 – отрезки, отсекаемые нейтральной осью от координатных осей.
– отрезки, отсекаемые нейтральной осью от координатных осей. Изобразим поперечное сечение бруса и построим нейтральную ось (рис. 3.24).
Изобразим поперечное сечение бруса и построим нейтральную ось (рис. 3.24).
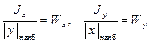 , то получим
, то получим


 Далее рассмотрим кручение. Строим эпюру крутящих моментов
Далее рассмотрим кручение. Строим эпюру крутящих моментов  Как использовать полученные эпюры для оценки прочности и назначения поперечного сечения? Для этого изобразим любое сечение вала, в которой действуют М и и М к. Покажем плоскость М и и эпюру нормальных напряжений (рис. 3.28). Для этих же точек покажем эпюру касательных напряжений. Видно, что самая опасная точка находится на поверхности вала и в ней действуют σ наиб и τ наиб.
Как использовать полученные эпюры для оценки прочности и назначения поперечного сечения? Для этого изобразим любое сечение вала, в которой действуют М и и М к. Покажем плоскость М и и эпюру нормальных напряжений (рис. 3.28). Для этих же точек покажем эпюру касательных напряжений. Видно, что самая опасная точка находится на поверхности вала и в ней действуют σ наиб и τ наиб.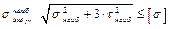

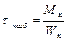 ,
,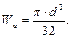

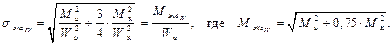

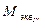 ≤ [ σ ]
≤ [ σ ]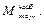
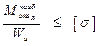
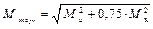 , и находим наибольшее значение.
, и находим наибольшее значение.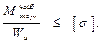
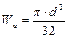 , отсюда,
, отсюда,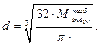
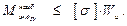
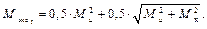 .
.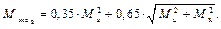
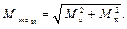
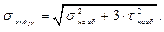 (3.4)
(3.4) (3.5)
(3.5)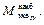 Так как N / A << M и / W и, то проверка на прочность всего вала производится в сечении с
Так как N / A << M и / W и, то проверка на прочность всего вала производится в сечении с 
 Механизм разрушения хорошо подтверждается, если рассмотреть усталостный излом – поверхность раздела, возникающую при усталостном разрушении объекта (рис. 4.2). В сечении можно видеть две зоны: зону 1 и 2.
Механизм разрушения хорошо подтверждается, если рассмотреть усталостный излом – поверхность раздела, возникающую при усталостном разрушении объекта (рис. 4.2). В сечении можно видеть две зоны: зону 1 и 2.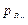 , при изгибе –
, при изгибе – 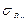 , при кручении –
, при кручении – 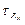 , при растяжении-сжатии –
, при растяжении-сжатии – 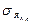 .
.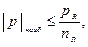
 Цикл напряжений – совокупность последовательных значений напряжений за один период их изменения от одного крайнего значения до другого и обратно.
Цикл напряжений – совокупность последовательных значений напряжений за один период их изменения от одного крайнего значения до другого и обратно.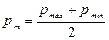 – среднее напряжение цикла или постоянная составляющая цикла напряжении;
– среднее напряжение цикла или постоянная составляющая цикла напряжении;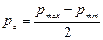 – амплитуда напряжении цикла или переменная составляющая цикла напряжений;
– амплитуда напряжении цикла или переменная составляющая цикла напряжений;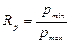 – коэффициент асимметрии цикла напряжении (характеристика цикла)
– коэффициент асимметрии цикла напряжении (характеристика цикла)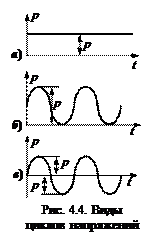 Рассмотрим примеры:
Рассмотрим примеры:
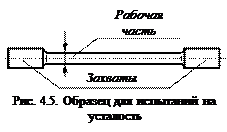
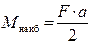 , а наибольшее напряжение –
, а наибольшее напряжение – 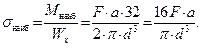 .
.

 1) при pRm = 0 – симметричный цикл, следовательно pR а = p –1;
1) при pRm = 0 – симметричный цикл, следовательно pR а = p –1;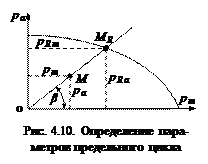 Изобразим ещё раз, диаграмму предельных амплитуд цикла (рис. 4.10).
Изобразим ещё раз, диаграмму предельных амплитуд цикла (рис. 4.10).